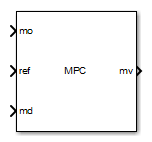
MPC Controller
Simulate model predictive controller
Libraries:
Model Predictive Control Toolbox
Description
The MPC Controller block receives the current measured output signal
(mo), reference signal (ref), and optional measured
disturbance signal (md). The block computes the optimal manipulated
variable (mv) by solving a quadratic programming problem using either the
default KWIK solver or a custom QP solver. For more information, see QP Solvers for Linear MPC.
To use the block in simulation and code generation, you must specify an
mpc object, which defines a model predictive controller. This
controller must have already been designed for the plant that it controls.
Because the MPC Controller block uses MATLAB Function blocks, it requires compilation each time you change the MPC object and block. Also, because MATLAB® does not allow compiled code to reside in any MATLAB product folder, you must use a non-MATLAB folder to work on your Simulink® model when you use MPC blocks.
Examples
Switching Controllers Based on Optimal Costs
You can switch between multiple MPC controllers based on their optimal objective function cost values.
Understanding Control Behavior by Examining Optimal Control Sequence
You can analyze the optimal control sequence computed by a model predictive controller at each sample time.
Improving Control Performance with Look-Ahead (Previewing)
Improve reference tracking and measured disturbance rejection using signal previewing.
Vary Input and Output Bounds at Run Time
You can vary the upper and lower bounds of plant inputs and outputs at run time.
Tuning MPC Controller Weights at Run-Time
Tune MPC Controller Weights at Run-Time in simulation.
Ports
Input
Required Inputs
Measured outputs, specified as a vector signal. The block uses the measured plant outputs to improve its state estimates. If your controller uses default state estimation, you must connect the measured plant outputs to the mo input port. If your controller uses custom state estimation, you must connect the estimated plant states to the x[k|k] input port.
Dependencies
To enable this port, clear the Use custom state estimation instead of using the built-in Kalman filter parameter.
Custom state estimate, specified as a vector signal. The block uses the connected state estimates instead of estimating the states using the built-in estimator. If your controller uses custom state estimation, you must connect the current state estimates to the x[k|k] input port. If your controller uses default state estimation, you must connect the measured output to the mo input port.
Even though noise model states (if any) are not used
in MPC optimization, the custom state vector must contain all the
states defined in the mpcstate object of the
controller, including the plant, disturbance, and noise model
states.
Use custom state estimates when an alternative estimation technique is considered superior to the built-in estimator or when the states are fully measurable.
Dependencies
To enable this port, select the Use custom state estimation instead of using the built-in Kalman filter parameter.
Plant output reference values, specified as a row vector signal or matrix signal.
To use the same reference values across the prediction horizon, connect ref to a row vector signal with Ny elements, where Ny is the number of output variables. Each element specifies the reference for an output variable.
To vary the references over the prediction horizon (previewing) from time k+1 to time k+p, connect ref to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the references for one prediction horizon step. If you specify fewer than p rows, the final references are used for the remaining steps of the prediction horizon.
Additional Inputs
If your controller prediction model has measured disturbances you must enable this port and connect to it a row vector or matrix signal.
To use the same measured disturbance values across the prediction horizon, connect md to a row vector signal with Nmd elements, where Nmd is the number of manipulated variables. Each element specifies the value for a measured disturbance.
To vary the disturbances over the prediction horizon (previewing) from time k to time k+p, connect md to a matrix signal with Nmd columns and up to p+1 rows. Here, k is the current time and p is the prediction horizon. Each row contains the disturbances for one prediction horizon step. If you specify fewer than p+1 rows, the final disturbances are used for the remaining steps of the prediction horizon.
Dependencies
To enable this port, select the Measured disturbances parameter.
Control signals used in the plant at the previous control interval, specified as a vector signal of length Nmv, where Nmv is the number of manipulated variables. Use this input port to improve state estimation accuracy when:
You know your controller is not always in control of the plant.
The actual MV signals applied to the plant can potentially differ from the values generated by the controller, such as in control signal saturation.
Controller state estimation assumes that the MVs are piecewise constant. Therefore, at time tk, the ext.mv value must contain the effective MVs between times tk–1 and tk. For example, if the MVs are actually varying over this interval, you might supply the time-averaged value evaluated at time tk.
Note
Connect ext.mv to the MV signals actually applied to the plant in the previous control interval. Typically, these MV signals are the values generated by the controller, though this is not always the case. For example, if your controller is offline and running in tracking mode (that is, the controller output is not driving the plant), then feeding the actual control signal to ext.mv can help achieve bumpless transfer when the controller is switched back online.
When the controller is driving the plant, insert a Memory block or Unit Delay block to feed back the MV signal applied to the plant at the previous control interval. This also avoids a direct feedthrough from the ext.mv inport to the mv outport, therefore preventing algebraic loops in the Simulink model.
For an example that uses the external manipulated variable input port for bumpless transfer, see Switch Controller Online and Offline with Bumpless Transfer.
Dependencies
To enable this port, select the External manipulated variable parameter.
To turn off the controller optimization calculations, connect switch to a nonzero signal.
Disabling optimization calculations reduces computational effort when the controller output is not needed, such as when the system is operating manually or another controller has taken over. However, the controller continues to update its internal state estimates in the usual way. Therefore, it is ready to resume optimization calculations whenever the switch signal returns to zero. While controller optimization is off, the block passes the current ext.mv signal to the controller output. If the ext.mv inport is not enabled, the controller output is held at the value it had when optimization was disabled.
For an example that uses the external manipulated variable input port for bumpless transfer, see Switch Controller Online and Offline with Bumpless Transfer.
Dependencies
To enable this port, select the Use external signal to enable or disable optimization parameter.
To specify manipulated variable targets, enable this input port, and connect a vector signal. To make a given manipulated variable track its specified target value, you must also specify a nonzero tuning weight for that manipulated variable.
The supplied mv.target values at run-time apply across the prediction horizon.
Dependencies
To enable this port, select the Targets for manipulated variables parameter.
Online Constraints
To specify run-time minimum output variable constraints, enable this input port. If
this port is disabled, the block uses the lower bounds specified in the
OutputVariables.Min property of its mpc controller object. If an output variable has no lower bound specified
in the controller object, then at run time the block ignores the corresponding connected
signal.
To change the bounds over the prediction horizon from time k+1 to time k+p, connect ymin to a matrix signal with Ny columns and up to p rows. Here, Ny is the number of plant outputs, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon. If there is only one output variable, and a vector signal with no more than p entries is connected, then these entries are used across the prediction horizon.
The ith column of the ymin signal corresponds
to the ith plant output, and replaces the
OutputVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar OutputVariables(i).Min in the mpc
object (a constant bound for the ith plant output to be applied
to all prediction steps)
| ymin Dimension | Replacement Behavior |
|---|---|
| Scalar ymin (single output, constant bound) | ymin replaces the constant bound defined in
OutputVariables(i).Min. |
| Column vector ymin (single output, time-varying bound) | ymin replaces the constant bound defined in
OutputVariables(i).Min with a time-varying
bound. |
| Row vector ymin (multiple outputs, constant bounds) | The ith element of ymin
replaces the constant bound defined in
OutputVariables(i).Min. |
| Matrix ymin (multiple outputs, time-varying bounds) | The ith column of ymin
replaces the constant bound defined in
OutputVariables(i).Min with a time-varying
bound. |
Vector OutputVariables(i).Min in the mpc
object (a time-varying bound for the ith plant output with
different values at different prediction steps)
| ymin Dimension | Replacement Behavior |
|---|---|
| Scalar ymin (single output, constant bound) | ymin replaces the first finite entry
in OutputVariables.Min and the remaining entries
in OutputVariables.Min shift up or down with the same
amount of displacement to retain the profile defined by the original
OutputVariables.Min vector. |
| Column vector ymin (single output, time-varying bound) | ymin replaces the time-varying bound defined in
OutputVariables(i).Min, and the original bound
profile is discarded. |
| Row vector ymin (multiple outputs, constant bounds) | The ith element of ymin
replaces the first finite entry
in OutputVariables(i).Min and the remaining
entries in OutputVariables(i).Min shift up or down
with the same amount of displacement to retain the profile defined by
the original OutputVariables(i).Min vector. |
| Matrix ymin (multiple outputs, time-varying bounds). | The ith column of ymin
replaces the time-varying bound defined in
OutputVariables(i).Min, and the original bound
profile is discarded. |
Dependencies
To enable this port, select the Lower OV limits parameter.
To specify run-time maximum output variable constraints, enable this input port. If
this port is disabled, the block uses the upper bounds specified in the
OutputVariables.Max property of its mpc controller object. If an output variable has no upper bound specified
in the controller object, then at run time the block ignores the corresponding connected
signal.
To change the bounds over the prediction horizon from time k+1 to time k+p, connect ymax to a matrix signal with Ny columns and up to p rows. Here, Ny is the number of plant outputs, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon. If there is only one output variable, and a vector signal with no more than p entries is connected, then these entries are used across the prediction horizon.
The ith column of the ymax signal corresponds
to the ith plant output, and replaces the
OutputVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar OutputVariables(i).Max in the mpc
object (a constant bound for the ith plant output to be applied
to all prediction steps)
| ymax Dimension | Replacement Behavior |
|---|---|
| Scalar ymax (single output, constant bound) | ymax replaces the constant bound defined in
OutputVariables(i).Max. |
| Column vector ymax (single output, time-varying bound) | ymax replaces the constant bound defined in
OutputVariables(i).Max with a time-varying
bound. |
| Row vector ymax (multiple outputs, constant bounds) | The ith element of ymax
replaces the constant bound defined in
OutputVariables(i).Max. |
| Matrix ymax (multiple outputs, time-varying bounds) | The ith column of ymax
replaces the constant bound defined in
OutputVariables(i).Max with a time-varying
bound. |
Vector OutputVariables(i).Max in the mpc
object (a time-varying bound for the ith plant output with
different values at different prediction steps)
| ymax Dimension | Replacement Behavior |
|---|---|
| Scalar ymax (single output, constant bound) | ymax replaces the first finite entry
in OutputVariables.Max and the remaining entries
in OutputVariables.Max shift up or down with the same
amount of displacement to retain the profile defined by the original
OutputVariables.Max vector. |
| Column vector ymax (single output, time-varying bound) | ymax replaces the time-varying bound defined in
OutputVariables(i).Max, and the original bound
profile is discarded. |
| Row vector ymax (multiple outputs, constant bounds) | The ith element of ymax
replaces the first finite entry
in OutputVariables(i).Max and the remaining
entries in OutputVariables(i).Max shift up or down
with the same amount of displacement to retain the profile defined by
the original OutputVariables(i).Max vector. |
| Matrix ymax (multiple outputs, time-varying bounds). | The ith column of ymax
replaces the time-varying bound defined in
OutputVariables(i).Max, and the original bound
profile is discarded. |
Dependencies
To enable this port, select the Upper OV limits parameter.
To specify run-time minimum manipulated variable constraints, enable this input port.
If this port is disabled, the block uses the lower bounds specified in the
ManipulatedVariables.Min property of its mpc controller object. If a manipulated variable has no lower bound
specified in the controller object, then at run time the block ignores the corresponding
connected signal.
To change the bounds over the prediction horizon from time k to time k+p-1, connect umin to a matrix signal with Nmv columns and up to p rows. Here, Nmv is the number of manipulated variables, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon. If there is only one manipulated variable, and a vector signal with no more than p entries is connected, then these entries are used across the prediction horizon.
The ith column of the umin signal corresponds
to the ith manipulated variable, and replaces the
ManipulatedVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar ManipulatedVariables(i).Min in the mpc
object (a constant bound for the ith manipulated variable to be
applied to all prediction steps)
| umin Dimension | Replacement Behavior |
|---|---|
| Scalar umin (single output, constant bound) | umin replaces the constant bound defined in
ManipulatedVariables(i).Min. |
| Column vector umin (single output, time-varying bound) | umin replaces the constant bound defined in
ManipulatedVariables(i).Min with a time-varying
bound. |
| Row vector umin (multiple outputs, constant bounds) | The ith element of umin
replaces the constant bound defined in
ManipulatedVariables(i).Min. |
| Matrix umin (multiple outputs, time-varying bounds) | The ith column of umin
replaces the constant bound defined in
ManipulatedVariables(i).Min with a time-varying
bound. |
Vector ManipulatedVariables(i).Min in the mpc
object (a time-varying bound for the ith manipulated variable
with different values at different prediction steps)
| umin Dimension | Replacement Behavior |
|---|---|
| Scalar umin (single output, constant bound) | umin replaces the first finite entry
in ManipulatedVariables.Min and the remaining
entries in ManipulatedVariables.Min shift up or down
with the same amount of displacement to retain the profile defined by
the original ManipulatedVariables.Min vector. |
| Column vector umin (single output, time-varying bound) | umin replaces the time-varying bound defined in
ManipulatedVariables(i).Min, and the original
bound profile is discarded. |
| Row vector umin (multiple outputs, constant bounds) | The ith component of umin
replaces the first finite entry
in ManipulatedVariables(i).Min and the remaining
entries in ManipulatedVariables(i).Min shift up or
down with the same amount of displacement to retain the profile defined
by the original ManipulatedVariables(i).Min
vector. |
| Matrix umin (multiple outputs, time-varying bounds). | The ith column of umin
replaces the time-varying bound defined in
ManipulatedVariables(i).Min, and the original
bound profile is discarded. |
Dependencies
To enable this port, select the Lower MV limits parameter.
To specify run-time maximum manipulated variable constraints, enable this input port.
If this port is disabled, the block uses the upper bounds specified in the
ManipulatedVariables.Max property of its mpc controller object. If a manipulated variable has no upper bound
specified in the controller object, then at run time the block ignores the corresponding
connected signal.
To change the bounds over the prediction horizon from time k to time k+p-1, connect umax to a matrix signal with Nmv columns and up to p rows. Here, Nmv is the number of manipulated variables, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon. If there is only one manipulated variable, and a vector signal with no more than p entries is connected, then these entries are used across the prediction horizon.
The ith column of the umax signal corresponds
to the ith manipulated variable, and replaces the
ManipulatedVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar ManipulatedVariables(i).Max in the mpc
object (a constant bound for the ith manipulated variable to be
applied to all prediction steps)
| umax Dimension | Replacement Behavior |
|---|---|
| Scalar umax (single output, constant bound) | umax replaces the constant bound defined in
ManipulatedVariables(i).Max. |
| Column vector umax (single output, time-varying bound) | umax replaces the constant bound defined in
ManipulatedVariables(i).Max with a time-varying
bound. |
| Row vector umax (multiple outputs, constant bounds) | The ith element of umax
replaces the constant bound defined in
ManipulatedVariables(i).Max. |
| Matrix umax (multiple outputs, time-varying bounds) | The ith column of umax
replaces the constant bound defined in
ManipulatedVariables(i).Max with a time-varying
bound. |
Vector ManipulatedVariables(i).Max in the mpc
object (a time-varying bound for the ith manipulated variable
with different values at different prediction steps)
| umax Dimension | Replacement Behavior |
|---|---|
| Scalar umax (single output, constant bound) | umax replaces the first finite entry
in ManipulatedVariables.Max and the remaining
entries in ManipulatedVariables.Max shift up or down
with the same amount of displacement to retain the profile defined by
the original ManipulatedVariables.Max vector. |
| Column vector umax (single output, time-varying bound) | umax replaces the time-varying bound defined in
ManipulatedVariables(i).Max, and the original
bound profile is discarded. |
| Row vector umax (multiple outputs, constant bounds) | The ith element of umax
replaces the first finite entry
in ManipulatedVariables(i).Max and the remaining
entries in ManipulatedVariables(i).Max shift up or
down with the same amount of displacement to retain the profile defined
by the original ManipulatedVariables(i).Max
vector. |
| Matrix umax (multiple outputs, time-varying bounds). | The ith column of umax
replaces the time-varying bound defined in
ManipulatedVariables(i).Max, and the original
bound profile is discarded. |
Dependencies
To enable this port, select the Upper MV limits parameter.
Manipulated variable constraint matrix, specified as an Nc-by-Nmv matrix signal, where Nc is the number of mixed input/output constraints and Nmv is the number of manipulated variables.
If you define E in the mpc object, you must
connect a signal to the E input port. Otherwise, connect a zero
matrix with the correct size.
To specify run-time mixed input/output constraints, use the E input port
along with the F, G, and
S ports. These constraints replace the mixed input/output
constraints previously set using setconstraint. For more information on mixed input/output constraints,
see Constraints on Linear Combinations of Inputs and Outputs.
The number of mixed input/output constraints cannot change at run time. Therefore,
Nc must match the number of rows in
the E matrix you specified using
setconstraint.
Dependencies
To enable this port, select the Custom constraints parameter.
Controlled output constraint matrix, specified as an
Nc-by-Ny
matrix signal, where Nc is the number of mixed
input/output constraints and Ny is the number
of plant outputs. If you define F in the mpc
object, you must connect a signal to the F input port with same
number of rows. Otherwise, connect a zero matrix with the correct size.
To specify run-time mixed input/output constraints, use the F input port
along with the E, G, and
S ports. These constraints replace the mixed input/output
constraints previously set using setconstraint. For more information on mixed input/output constraints,
see Constraints on Linear Combinations of Inputs and Outputs.
The number of mixed input/output constraints cannot change at run time. Therefore,
Nc must match the number of rows in
the F matrix you specified using
setconstraint.
Dependencies
To enable this port, select the Custom constraints parameter.
Custom constraint vector, specified as a row vector signal of length
Nc, where
Nc is the number of mixed input/output
constraints. If you define G in the mpc object,
you must connect a signal to the G input port with same number of
rows. Otherwise, connect a zero matrix with the correct size.
To specify run-time mixed input/output constraints, use the G input port
along with the E, F, and
S ports. These constraints replace the mixed input/output
constraints previously set using setconstraint. For more information on mixed input/output constraints,
see Constraints on Linear Combinations of Inputs and Outputs.
The number of mixed input/output constraints cannot change at run time. Therefore,
Nc must match the number of rows in
the G matrix you specified using
setconstraint.
Dependencies
To enable this port, select the Custom constraints parameter.
Measured disturbance constraint matrix, specified as an
Nc-by-nN
matrix signal, where Nc is the number of mixed
input/output constraints, and Nv is the number
of measured disturbances. If you define S in the
mpc object, you must connect a signal to the
S input port with same number of rows. Otherwise, connect a
zero matrix with the correct size.
To specify run-time mixed input/output constraints, use the S input port
along with the E, F, and
G ports. These constraints replace the mixed input/output
constraints previously set using setconstraint. For more information on mixed input/output constraints,
see Constraints on Linear Combinations of Inputs and Outputs.
The number of mixed input/output constraints cannot change at run time. Therefore,
Nc must match the number of rows in
the G matrix you specified using
setconstraint.
Dependencies
To enable this port, select the Custom constraints parameter. This port is added only if the mpc object has measured disturbances.
Online Tuning Weights
To specify run-time output variable tuning weights, enable this input port. If this port is disabled, the block uses the tuning weights specified in the Weights.OutputVariables property of its controller object. These tuning weights penalize deviations from output references.
If the MPC controller object uses constant output tuning weights over the prediction horizon, you can specify only constant output tuning weights at runtime. Similarly, if the MPC controller object uses output tuning weights that vary over the prediction horizon, you can specify only time-varying output tuning weights at runtime.
To use constant tuning weights over the prediction horizon, connect y.wt to a row vector signal with Ny elements, where Ny is the number of outputs. Each element specifies a nonnegative tuning weight for an output variable. For more information on specifying tuning weights, see Tune Weights.
To vary the tuning weights over the prediction horizon from time k+1 to time k+p, connect y.wt to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the tuning weights for one prediction horizon step. If you specify fewer than p rows, the tuning weights in the final row apply for the remainder of the prediction horizon. For more information on varying weights over the prediction horizon, see Setting Time-Varying Weights and Constraints with MPC Designer.
Dependencies
To enable this port, select the OV weights parameter.
To specify run-time manipulated variable tuning weights, enable this input port. If
this port is disabled, the block uses the tuning weights specified in the
Weights.ManipulatedVariables property of its controller object.
These tuning weights penalize deviations from MV targets.
If the MPC controller object uses constant manipulated variable tuning weights over the prediction horizon, you can specify only constant manipulated variable tuning weights at runtime. Similarly, if the MPC controller object uses manipulated variable tuning weights that vary over the prediction horizon, you can specify only time-varying manipulated variable tuning weights at runtime.
To use the same tuning weights over the prediction horizon, connect u.wt to a row vector signal with Nmv elements, where Nmv is the number of manipulated variables. Each element specifies a nonnegative tuning weight for a manipulated variable. For more information on specifying tuning weights, see Tune Weights.
To vary the tuning weights over the prediction horizon from time k to time k+p-1, connect u.wt to a matrix signal with Nmv columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the tuning weights for one prediction horizon step. If you specify fewer than p rows, the tuning weights in the final row apply for the remainder of the prediction horizon. For more information on varying weights over the prediction horizon, see Setting Time-Varying Weights and Constraints with MPC Designer.
Dependencies
To enable this port, select the MV weights parameter.
To specify run-time manipulated variable rate tuning weights, enable this input port. If this port is disabled, the block uses the tuning weights specified in the Weights.ManipulatedVariablesRate property of its controller object. These tuning weights penalize large changes in control moves.
If the MPC controller object uses constant manipulated variable rate tuning weights over the prediction horizon, you can specify only constant manipulated variable tuning rate weights at runtime. Similarly, if the MPC controller object uses manipulated variable rate tuning weights that vary over the prediction horizon, you can specify only time-varying manipulated variable rate tuning weights at runtime.
To use the same tuning weights over the prediction horizon, connect du.wt to a row vector signal with Nmv elements, where Nmv is the number of manipulated variables. Each element specifies a nonnegative tuning weight for a manipulated variable rate. For more information on specifying tuning weights, see Tune Weights.
To vary the tuning weights over the prediction horizon from time k to time k+p-1, connect du.wt to a matrix signal with Nmv columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the tuning weights for one prediction horizon step. If you specify fewer than p rows, the tuning weights in the final row apply for the remainder of the prediction horizon. For more information on varying weights over the prediction horizon, see Setting Time-Varying Weights and Constraints with MPC Designer.
Dependencies
To enable this port, select the MVRate weights parameter.
To specify a run-time slack variable tuning weight, enable this input port and connect a scalar signal. If this port is disabled, the block uses the tuning weight specified in the Weights.ECR property of its controller object.
The slack variable tuning weight has no effect unless your controller object defines soft constraints whose associated ECR values are nonzero. If there are soft constraints, increasing the ecr.wt value makes these constraints relatively harder. The controller then places a higher priority on minimizing the magnitude of the predicted worst-case constraint violation.
Dependencies
To enable this port, select the ECR weight parameter.
Online Horizons
Prediction horizon, specified as positive integer signal. The prediction horizon signal value must be less than or equal to the Maximum prediction horizon parameter.
At run time, the values of p overrides the default prediction horizon specified in the controller object. For more information, see Adjust Horizons at Run Time.
Dependencies
To enable this port, select the Adjust prediction horizon and control horizon at run time parameter.
Control horizon, specified as one of the following:
Positive integer signal less than or equal to the prediction horizon.
Vector signal of positive integers specifying blocking interval lengths. For more information, see Manipulated Variable Blocking.
At run time, the values of m overrides the default control horizon specified in the controller object. For more information, see Adjust Horizons at Run Time.
Dependencies
To enable this port, select the Adjust prediction horizon and control horizon at run time parameter.
Output
Required Output
Optimal manipulated variable control action, output as a column vector signal of length Nmv, where Nmv is the number of manipulated variables.
If the solver converges to a local optimum solution (qp.status is positive), then mv contains the optimal solution.
If the solver fails (qp.status is negative), then mv remains at its most recent successful solution; that is, the controller output freezes.
If the solver reaches the maximum number of iterations without finding an optimal solution
(qp.status is zero) and the
Optimization.UseSuboptimalSolution property of the controller
is:
true, then mv contains the suboptimal solutionfalse, then mv then mv remains at its most recent successful solution
Additional Outputs
Objective function cost, output as a nonnegative scalar signal. The cost quantifies the degree to which the controller has achieved its objectives. The cost value is calculated using the scaled MPC cost function in which every term is offset-free and dimensionless.
The cost value is only meaningful when the qp.status output is nonnegative.
Dependencies
To enable this port, select the Optimal cost parameter.
Optimization status, output as an integer signal.
If the controller solves the QP problem for a given control interval, the qp.status output returns the number of QP solver iterations used in computation. This value is a finite, positive integer and is proportional to the time required for the calculations. Therefore, a large value means a relatively slow block execution for this time interval.
The QP solver can fail to find an optimal solution for the following reasons:
qp.status =
0— The QP solver cannot find a solution within the maximum number of iterations specified in thempcobject. In this case, if theOptimizer.UseSuboptimalSolutionproperty of the controller isfalse, the block holds its mv output at the most recent successful solution. Otherwise, it uses the suboptimal solution found during the last solver iteration.qp.status =
-1— The QP solver detects an infeasible QP problem. See Monitoring Optimization Status to Detect Controller Failures for an example where a large, sustained disturbance drives the output variable outside its specified bounds. In this case, the block holds its mv output at the most recent successful solution.qp.status =
-2— The QP solver has encountered numerical difficulties in solving a severely ill-conditioned QP problem. In this case, the block holds its mv output at the most recent successful solution.
In a real-time application, you can use qp.status to set an alarm or take other special action.
Dependencies
To enable this port, select the Optimization status parameter.
Estimated controller states at each control instant, returned as a vector signal. The estimated states include the plant, disturbance, and noise model states. If custom state estimation is used, this output signal has the same value as the x[k|k] input signal.
Dependencies
To enable this port, select the Estimated controller states parameter.
Optimal Sequences
Optimal manipulated variable sequence, returned as a matrix signal with p+1 rows and Nmv columns, where p is the prediction horizon and Nmv is the number of manipulated variables.
The first p rows of mv.seq contain the calculated optimal manipulated variable values from current time k to time k+p-1. The first row of mv.seq contains the current manipulated variable values (output mv). Since the controller does not calculate optimal control moves at time k+p, the final two rows of mv.seq are identical.
Dependencies
To enable this port, select the Optimal control sequence parameter.
Optimal prediction model state sequence, returned as a matrix signal with p+1 rows and Nx columns, where p is the prediction horizon and Nx is the number of states.
The first row of x.seq contains the current estimated state values, either from the built-in state estimator or from the custom state estimation block input x[k|k]. The next p rows of x.seq contain the calculated optimal state values from time k+1 to time k+p.
Dependencies
To enable this port, select the Optimal state sequence parameter.
Optimal output variable sequence, returned as a matrix signal with p+1 rows and Ny columns, where p is the prediction horizon and Ny is the number of output variables.
The first p rows of y.seq contain the calculated optimal output values from current time k to time k+p-1. The first row of y.seq is computed based on the current estimated states and the current measured disturbances (first row of input md). Since the controller does not calculate optimal output values at time k+p, the final two rows of y.seq are identical.
Dependencies
To enable this port, select the Optimal output sequence parameter.
Parameters
Specify an mpc object that defines an implicit MPC
controller by entering the name of an mpc object from the
MATLAB workspace.
Programmatic Use
Block Parameter:
mpcobj |
| Type: string, character vector |
Default:
"" |
Specify the initial controller state. If you leave this parameter blank, the block uses the
nominal values defined in the Model.Nominal property of the
mpc object. To override the default, create an mpcstate object in your workspace, and enter its name in the
field.
Use this parameter to make sure that the controller state reflects the state of the
plant at the start of your simulation, to the best of your knowledge. This initial state
can differ from the nominal state defined in the mpc object.
If custom state estimation is enabled, the block ignores the Initial Controller State parameter.
Programmatic Use
Block Parameter: x0 |
| Type: string, character vector |
Default: "" |
To interactively modify the controller specified using the MPC Controller parameter, open the MPC Designer app by clicking Design. For example, you can:
Import a new prediction model.
Change horizons, constraints, and weights.
Evaluate MPC performance with a linear plant.
Export the updated controller to the MATLAB workspace.
If you have an existing mpc object in the MATLAB workspace, specify the name of that object using the MPC
Controller parameter.
If you do not have an existing mpc object in the MATLAB workspace, leave the MPC Controller parameter empty.
With the MPC Controller block connected to the plant, open MPC
Designer by clicking Design. Using the app,
linearize the Simulink model at a specified operating point, and design your controller. To use
this design approach, you must have Simulink
Control Design™ software. For more information, see Design MPC Controller in Simulink and Linearize Simulink Models Using MPC Designer.
Once you specify a controller using the MPC Controller parameter, you can review your design for run-time stability and robustness issues by clicking Review. For more information, see Review Model Predictive Controller for Stability and Robustness Issues.
General Tab
If your controller has measured disturbances, you must select this parameter to add the md output port to the block.
Programmatic Use
Block Parameter:
md_inport |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"on" |
Select this parameter to add the ext.mv input port to the block.
Programmatic Use
Block Parameter: mv_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the mv.target input port to the block.
Programmatic Use
Block Parameter: uref_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the cost output port to the block.
Programmatic Use
Block Parameter:
return_cost |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the qp.status output port to the block.
Programmatic Use
Block Parameter: return_qpstatus |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the est.state output port to the block.
Programmatic Use
Block Parameter: return_state |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the mv.seq output port to the block.
Programmatic Use
Block Parameter: return_mvseq |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the x.seq output port to the block.
Programmatic Use
Block Parameter: return_xseq |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the y.seq output port to the block.
Programmatic Use
Block Parameter:
return_ovseq |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to remove the mo input port and add the x[k|k] input port.
Programmatic Use
Block Parameter: state_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Online Features Tab
Select this parameter to add the ymin input port to the block.
Programmatic Use
Block Parameter: ymin_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the ymax input port to the block.
Programmatic Use
Block Parameter: ymax_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the umin input port to the block.
Programmatic Use
Block Parameter: umin_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the umax input port to the block.
Programmatic Use
Block Parameter: umax_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the E, F, G, and S input ports to the block.
For more information, see Constraints on Linear Combinations of Inputs and Outputs and Update Mixed Input/Output Constraints at Run Time.
Programmatic Use
Block Parameter:
cc_inport |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the y.wt input port to the block.
Programmatic Use
Block Parameter: ywt_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the u.wt input port to the block.
Programmatic Use
Block Parameter: uwt_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the du.wt input port to the block.
Programmatic Use
Block Parameter: duwt_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the ecr.wt input port to the block.
Programmatic Use
Block Parameter: rhoeps_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the p and m input port to the block.
Programmatic Use
Block Parameter: pm_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the p and m input port to the block.
Dependencies
To enable this parameter, select the Adjust prediction horizon and control horizon at run time parameter.
Programmatic Use
Block Parameter: MaximumP |
| Type: string, character vector |
Default: "10" |
Default Conditions Tab
Default block sample time for performing simulation, trimming, or linearization using the MPC Designer app. You must specify a sample time that is compatible with your Simulink model design.
Dependencies
This parameter applies only when the MPC Controller parameter is empty and you open MPC Designer using the Design button.
Programmatic Use
Block Parameter:
n_ts |
| Type: string, character vector |
Default:
"1" |
Default prediction horizon for performing simulation, trimming, or linearization using the MPC Designer app. You must specify a prediction horizon that is compatible with your Simulink model design.
Dependencies
This parameter applies only when the MPC Controller parameter is empty and you open MPC Designer using the Design button.
Programmatic Use
Block Parameter:
n_p |
| Type: string, character vector |
Default:
"10" |
Default number of manipulated variables for performing simulation, trimming, or linearization using the MPC Designer app. You must specify a value that is compatible with your Simulink model design.
Dependencies
This parameter applies only when the MPC Controller parameter is empty and you open MPC Designer using the Design button.
Programmatic Use
Block Parameter:
n_mv |
| Type: string, character vector |
Default:
"1" |
Default number of measured disturbances for performing simulation, trimming, or linearization using the MPC Designer app. You must specify a value that is compatible with your Simulink model design.
Dependencies
This parameter applies only when the MPC Controller parameter is empty and you open MPC Designer using the Design button.
To use this parameter, you must select the Measured disturbance parameter.
Programmatic Use
Block Parameter:
n_md |
| Type: string, character vector |
Default:
"1" |
Default number of unmeasured disturbances for performing simulation, trimming, or linearization using the MPC Designer app. You must specify a value that is compatible with your Simulink model design.
Dependencies
This parameter applies only when the MPC Controller parameter is empty and you open MPC Designer using the Design button.
Programmatic Use
Block Parameter:
n_ud |
| Type: string, character vector |
Default:
"0" |
Default number of measured outputs for performing simulation, trimming, or linearization using the MPC Designer app. You must specify a value that is compatible with your Simulink model design.
Dependencies
This parameter applies only when the MPC Controller parameter is empty and you open MPC Designer using the Design button.
Programmatic Use
Block Parameter:
n_mo |
| Type: string, character vector |
Default:
"1" |
Default number of unmeasured outputs for performing simulation, trimming, or linearization using the MPC Designer app. You must specify a value that is compatible with your Simulink model design.
Dependencies
This parameter applies only when the MPC Controller parameter is empty and you open MPC Designer using the Design button.
Programmatic Use
Block Parameter:
n_uo |
| Type: string, character vector |
Default:
"0" |
Others Tab
Specify the block data type of the manipulated variables as one of the following:
double— Double-precision floating pointsingle— Single-precision floating pointIf you are implementing the block on a single-precision target, specify the output data type as
single.data type expression— An expression that evaluates to eitherdoubleorsingle. For more information, see Control Data Types of Signals (Simulink).
Programmatic Use
Block Parameter: BlockDataType |
| Type: string, character vector |
Values:
"double", "single", data type
expression |
Default: "double" |
Select this parameter to inherit the sample time of the parent subsystem as the block sample time. Doing so allows you to conditionally execute this block inside Function-Call Subsystem (Simulink) or Triggered Subsystem (Simulink) blocks. For an example, see Using MPC Controller Block Inside Function-Call and Triggered Subsystems.
Note
You must execute Function-Call Subsystem or Triggered Subsystem blocks at the sample rate of the controller. Otherwise, you can see unexpected results for two reasons.
The first element of the MV rate vector (which is the difference between the current and the last value of the manipulated variable) is normally weighted and constrained assuming that the last MV value occurred in the past at the sample time specified in the MPC object, and when the block is executed with a different sample rate, this assumption no longer holds.
The built-in Kalman estimator uses the sample time specified in the MPC object to provide an estimation of the current state to the MPC optimization problem, so when the block is executed with a different sample time, the estimated state is no longer correct.
If you clear this parameter (default), the sample time of the block is inherited from the controller object.
To view the sample time of a block, in the Simulink model window, on the Debug tab, under Information Overlays, select either colors or Text. For more information, see View Sample Time Information (Simulink).
Programmatic Use
Block Parameter:
SampleTimeInherited |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the switch input port to the block.
Programmatic Use
Block Parameter: switch_inport |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.
Version History
Introduced before R2006aThe signal dimensions of the mv.seq output port of the MPC
Controller block have changed. Previously, this signal was a
p-by-Nmv matrix, where
p is the prediction horizon and
Nmv is the number of manipulated variables. Now,
mv.seq is a
(p+1)-by-Nmv matrix, where
row p+1 duplicates row p.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)