Inverse Park Transform

Implement dq to αβ transformation

Since R2020a

• 

Libraries:
Motor Control Blockset / Controls / Math Transforms
Motor Control Blockset HDL Support / Controls / Math Transforms

Description

The Inverse Park Transform block computes the inverse Park transformation of the orthogonal direct (d) and quadrature (q) axes components or the multiplexed dq0 components in the rotating dq reference frame.

You can configure the block to align either the d- or q-axis with the α-axis at time t = 0.

The block accepts the following inputs:

• Either d-q axes components or multiplexed components dq0 in the rotating reference frame. Use the Number of inputs parameter to use either two or three inputs.

• Sine and cosine values of the corresponding angles of transformation.

When using two-input configuration, it outputs the two-phase orthogonal components in the stationary αβ reference frame. When using three-input configuration, it outputs multiplexed components αβ0.

For a balanced system, the zero component is equal to zero.

The figures show a rotating dq reference frame and the α-β axes components in an αβ reference frame for when:

• The d-axis aligns with the α-axis.

  

• The q-axis aligns with the α-axis.

  

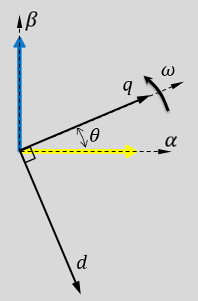
  In both cases, the angle θ = ωt, where:

  • θ is the angle between the α- and d-axes for the d-axis alignment or the angle between the α- and q-axes for the q-axis alignment. It indicates the angular position of the rotating dq reference frame with respect to the α-axis.

  • ω is the rotational speed of the d-q reference frame.

  • t is the time, in seconds, from the initial alignment.

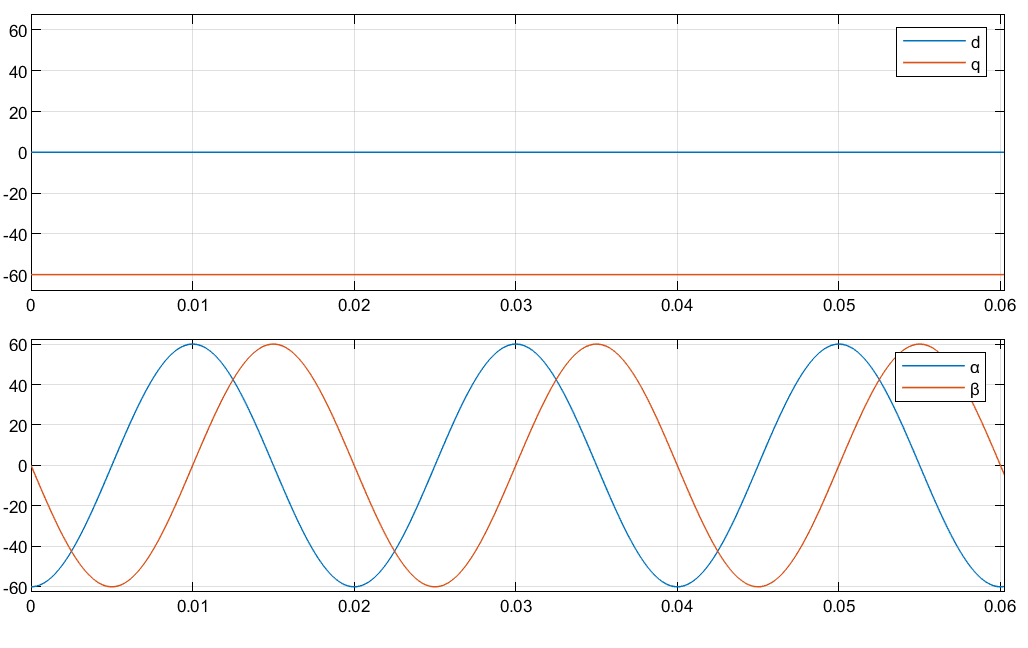
The figures show the time-response of the individual components of the αβ and dq reference frames when:

• The d-axis aligns with the α-axis.

  

• The q-axis aligns with the α-axis.

  

Equations

The following equations describe how the block implements inverse Park transformation.

• When the d-axis aligns with the α-axis.

  $\left[\begin{array}{c}{f}_{\alpha }\\ f_{\beta }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{f}_d\\ f_q\end{array}\right]$

• When the q-axis aligns with the α-axis.

  $\left[\begin{array}{c}{f}_{\alpha }\\ f_{\beta }\end{array}\right]=\left[\begin{array}{cc}\sin \theta & \cos \theta \\ -\cos \theta & \sin \theta \end{array}\right]\left[\begin{array}{c}{f}_d\\ f_q\end{array}\right]$

where:

• $$f_d$$ and $f_q$ are the direct and quadrature axis orthogonal components in the rotating dq reference frame.

• $f_{\alpha }$ and $f_{\beta }$ are the two-phase orthogonal components in the stationary αβ reference frame.

Examples

Field-Oriented Control of Induction Motor Using Speed Sensor

Implements the field-oriented control (FOC) technique to control the speed of a three-phase AC induction motor (ACIM). The FOC algorithm requires rotor speed feedback, which is obtained in this example by using a quadrature encoder sensor. For details about FOC, see Field-Oriented Control (FOC).

• Open Model

Field-Weakening Control (with MTPA) of PMSM

Implements the field-oriented control (FOC) technique to control the torque and speed of a three-phase permanent magnet synchronous motor (PMSM). The FOC algorithm requires rotor position feedback, which is obtained by a quadrature encoder sensor. For details about FOC, see Field-Oriented Control (FOC).

• Open Model

Field-Oriented Control of PMSM Using Hall Sensor

Implements the field-oriented control (FOC) technique to control the speed of a three-phase permanent magnet synchronous motor (PMSM). The FOC algorithm requires rotor position feedback, which is obtained by a Hall sensor. For details about FOC, see Field-Oriented Control (FOC).

• Open Model

Ports

Input

d — Axis component

scalar

Direct axis component, d, in the rotating dq reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Two inputs.

Data Types: single | double | fixed point

q — Axis component

scalar

Quadrature axis component, q, in the rotating dq reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Two inputs.

Data Types: single | double | fixed point

dq0 — Axis components

scalar

Multiplexed direct axis component, d, quadrature axis component, q, and the 0 component in the rotating dq reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Three inputs.

Data Types: single | double | fixed point

sin θ_e — Sine value of rotational angle

scalar

Sine value of the angle of transformation, θ_e. θ_e is the angle between the rotating reference frame and the α-axis.

Data Types: single | double | fixed point

cos θ_e — Cosine value of rotational angle

scalar

Cosine value of the angle of transformation, θ_e. θ_e is the angle between the rotating reference frame and the α-axis.

Data Types: single | double | fixed point

Output

α — Axis component

scalar

Alpha-axis component, α, in the stationary αβ reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Two inputs.

Data Types: single | double | fixed point

β — Axis component

scalar

Beta-axis component, β, in the stationary αβ reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Two inputs.

Data Types: single | double | fixed point

αβ0 — Axis components

scalar

Multiplexed alpha-axis component, α and beta-axis component, β and 0 component, in the stationary αβ reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Three inputs.

Data Types: single | double | fixed point

Parameters

Number of inputs — Number of block inputs

Two inputs (default) | Three inputs

Select the number of inputs that you can specify:

• Two inputs — Configure the block to accept two separate input signals d and q. The block generates two separate output signals α and β.

• Three inputs — Configure the block to accept a multiplexed input containing d,q, and 0 signals. The block generates a multiplexed output containing α, β, and 0 signals.

Alpha (phase-a) axis alignment — dq reference frame alignment

D-axis (default) | Q-axis

Align either the d- or q-axis of the rotating reference frame to the α-axis of the stationary reference frame.

Theta input — Type of position input

Sine and Cosine electrical position (default) | Electrical position

Type of position (theta) input:

• Sine and Cosine electrical position — Configure the block to directly accept sinθ_e and cosθ_e inputs.

• Electrical position — Configure the block to accept the electrical position (θ_e) input. The block internally computes the sinθ_e and cosθ_e signals from the θ_e input.

Theta units — Unit of electrical position input

Per-unit (default) | Radians | Degrees

Unit of the electrical position input (θ_e).

Dependencies

To enable this parameter, set Theta input to Electrical position.

Number of data points for lookup table — Size of lookup table array

1024 (default) | scalar

Size of the lookup table array that the block uses to compute sinθ_e and cosθ_e signals from the θ_e input. You can specify a value between 125 and 4095.

Dependencies

To enable this parameter, set Theta input to Electrical position.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
FlattenHierarchy	Remove Inverse Park Transform block hierarchy from generated HDL code. The default is inherit. See also FlattenHierarchy (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).
SharingFactor	Number of functionally equivalent resources to map to a single shared resource. The default is 0. See also Resource Sharing (HDL Coder).

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Version History

Introduced in R2020a