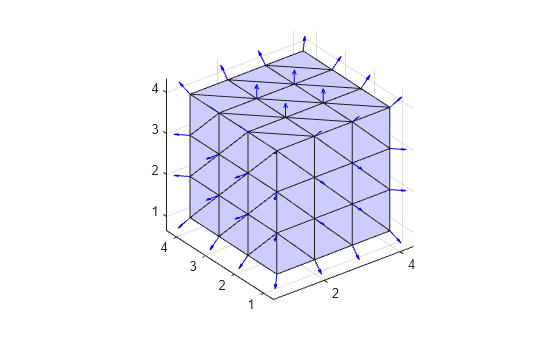
vertexNormal
Triangulation vertex normal
Description
V = vertexNormal( returns the unit
normal vectors to all vertices in a 3-D surface triangulation. TR)V
is a three-column matrix with each row containing the unit normal coordinates
corresponding to the vertices in TR.Points.
Examples
Input Arguments
Extended Capabilities
Version History
Introduced in R2013a