solve
Description
Examples
Create an ode object to integrate the function dydt = @(t,y) (1/2)*t^2. Specify the initial value of dydt as 0.
F = ode(ODEFcn=@(t,y) (1/2)*t^2,InitialValue=0);
Integrate the ode object by using the solve method. Specify a vector of times using linspace to evaluate the solution at specific time points in the interval [0 5].
t = linspace(0,5); S = solve(F,t)
S =
ODEResults with properties:
Time: [0 0.0505 0.1010 0.1515 0.2020 0.2525 0.3030 0.3535 0.4040 0.4545 0.5051 0.5556 0.6061 0.6566 0.7071 0.7576 0.8081 0.8586 0.9091 0.9596 1.0101 1.0606 1.1111 1.1616 1.2121 1.2626 1.3131 1.3636 1.4141 1.4646 1.5152 1.5657 … ] (1×100 double)
Solution: [0 2.1471e-05 1.7177e-04 5.7972e-04 0.0014 0.0027 0.0046 0.0074 0.0110 0.0157 0.0215 0.0286 0.0371 0.0472 0.0589 0.0725 0.0879 0.1055 0.1252 0.1473 0.1718 0.1988 0.2286 0.2612 0.2968 0.3355 0.3774 0.4226 0.4713 0.5237 … ] (1×100 double)
Plot the results.
plot(S.Time,S.Solution,"-o")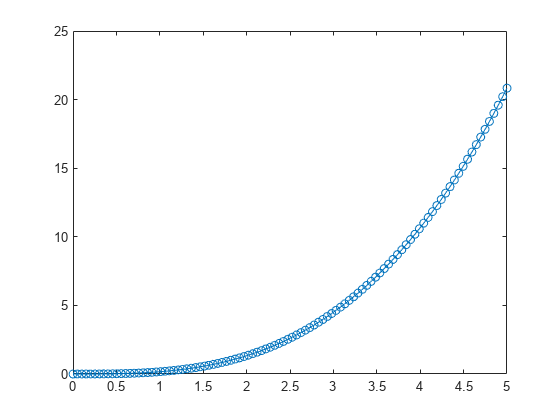
Integrate the ode object again, this time specifying time points in the interval [-5 5]. Even though the initial value of dydt is applied at F.InitialTime=0 by default, the solve method can evaluate the solution before the initial time.
t2 = linspace(-5,5);
S2 = solve(F,t2);
plot(S2.Time,S2.Solution,"-o")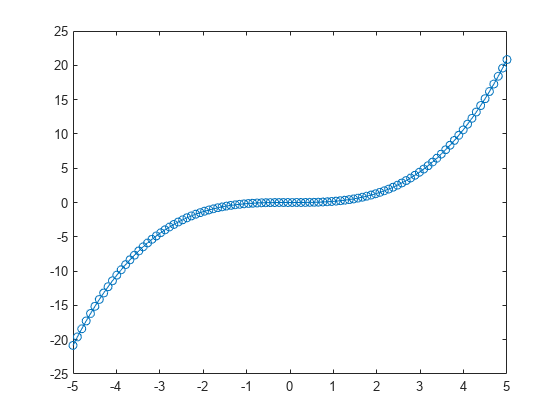
Create an ode object to integrate this system of equations.
Specify initial values of and .
F = ode(ODEFcn=@(t,y) [y(2); -y(1)],InitialValue=[0 1]);
Integrate the ode object over the interval [0 2*pi] by using the solve method. Plot the results.
S = solve(F,0,2*pi);
plot(S.Time,S.Solution,"-o")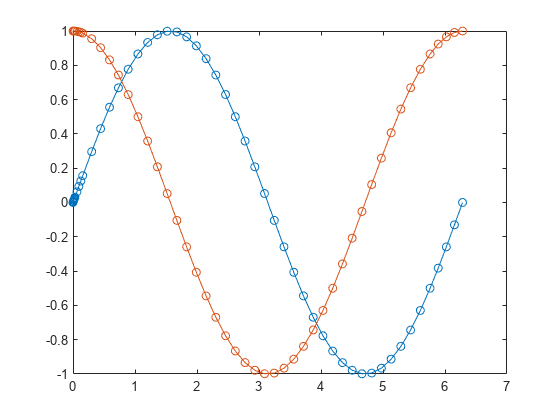
Integrate the ode object again, this time specifying Refine=6 to generate additional solution points in each time step.
S2 = solve(F,0,2*pi,Refine=6);
plot(S2.Time,S2.Solution,"-o")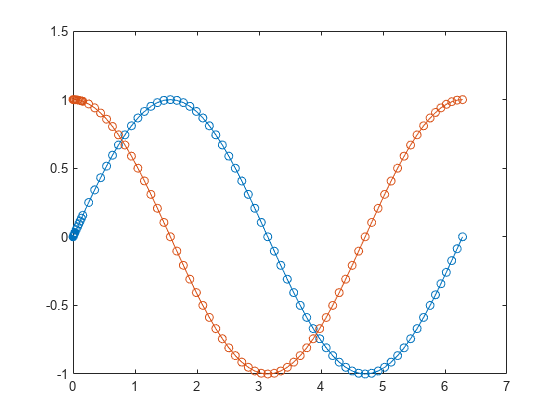
Input Arguments
ODE problem to solve, specified as an ode
object.
Time points to compute solution, specified as a vector with real elements. The
solver returns the solution evaluated at the given time points. However, the solver does
not step precisely to each point specified in t. Instead, the solver
uses its own internal steps to compute the solution, and then evaluates the solution at
the requested points in t. The solutions produced at the specified
points are of the same order of accuracy as the solutions computed at each internal
step.
The time points you specify in t are not bound by the value of
the InitialTime property of the ode object
F. You can specify time values before or after the value of
InitialTime.
The solver uses the values in t to calculate suitable values for
the F.SolverOptions.InitialStep and
F.SolverOptions.MaxStep options:
The specified time points give an indication of the scale for the problem, which can affect the value of
InitialStepused by the solver. Therefore, specifying the initial and final time points of the interval witht0,tfcan lead to different integration results compared to specifying a vector of times.The solver uses the initial and final time points to calculate the maximum step size
MaxStep. Therefore, changing the initial or final values intcan cause the solver to use a different step sequence, which might change the solution.
Example: S = solve(F,1:10) solves the ODE problem represented by
F at the time points 1:10.
Interval of integration, specified as two real scalars that indicate the initial
(t0) and final (tf) time points. The solver
returns the solution evaluated at each internal integration step within the specified
time interval.
The time points you specify in t0 and tf are
not bound by the value of the InitialTime property of the
ode object F. You can specify time values before
or after the value of InitialTime.
The solver uses the initial and final time points to calculate the maximum step size
F.SolverOptions.MaxStep. Therefore, changing
t0 or tf can cause the solver to use a different
step sequence, which might change the solution.
Example: S = solve(F,1,10) solves the ODE problem represented by
F in the interval [1 10].
Solution refinement factor, specified as a scalar integer. The scalar specifies a factor by which the number of output points should increase in each step.
The default value of N for most solvers is 1,
but ode45 uses a default value of 4, while
ode78 and ode89 use a default value of
8. These solvers use a larger default value to compensate for their
tendency to take large steps.
If the refinement factor is
1, then the solver returns solutions only at the end of each step.If the refinement factor is greater than
1, then the solver subdivides each step intoNsmaller intervals and returns solutions at each point.
The extra values produced by the refinement factor are computed by means of continuous extension formulas. The solvers use these specialized formulas to obtain accurate solutions between computed time steps without significant increase in computation time.
Example: S = solve(F,1,10,Refine=5) solves the ODE problem
represented by F in the interval [1 10] and
returns 5 points per time step.
Output Arguments
Computed solution, returned as an ODEResults
object.
Version History
Introduced in R2023b
See Also
ode | solutionFcn | ODEResults | odextend
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)