Main Content

solutionFcn

Construct function that interpolates ODE solution

Since R2023b

collapse all in page

Syntax

fh = solutionFcn(F,tmin,tmax)
fh = solutionFcn(F,tmin,tmax,Name=Value)
[fh,S] = solutionFcn(___)

Description

fh = solutionFcn(F,tmin,tmax) creates a function handle fh that can interpolate the solution of the differential equation problem represented by F at any time t in the range tmin <= t <= tmax. The tmin and tmax arguments must satisfy tmin <= t0 <= tmax, where t0 is the value of F.InitialTime.

example

fh = solutionFcn(F,tmin,tmax,Name=Value) specifies options using one or more name-value arguments. For example, specify OutputVariables=[1 2] to limit the function handle fh to interpolate only the first two solution components.

example

[fh,S] = solutionFcn(___) also returns an ODEResults object S, obtained by solving the differential equation problem over the specified time interval.

example

Examples

collapse all

Open Live Script

Create an ode object for the equation @(t,y) y(1) with the initial value y=1.

F = ode(ODEFcn=@(t,y) y(1),InitialValue=1);

Create a function handle that can evaluate the solution at any time value in the range [0 10] by using the solutionFcn method. 

fh = solutionFcn(F,0,10);

Use linspace to generate 100 points, and then evaluate the solution at those points and plot the results.

t = linspace(0,10);
y = fh(t);
plot(t,y,"-o")

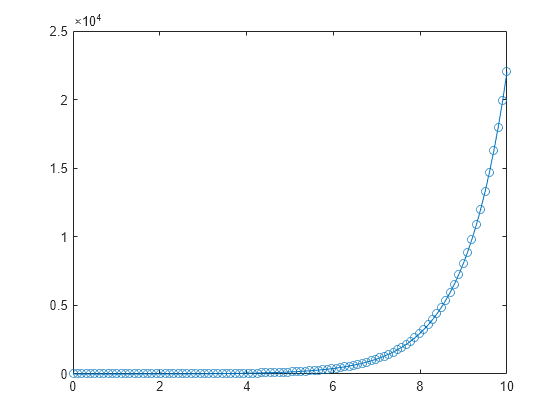
Figure contains an axes object. The axes object contains an object of type line.

Open Live Script

Create an ode object for the equations @(t,y) [y(2); 1000*(1-y(1)^2)*y(2)-y(1)] with the initial conditions [2 0]. Specify the solver as "stiff".

F = ode(ODEFcn=@(t,y) [y(2); 1000*(1-y(1)^2)*y(2)-y(1)],InitialValue=[2 0],Solver="stiff");

Create a function handle that can evaluate the solution of the problem in the interval [0 1000] by using the solutionFcn method.

  • Specify Extension="on" to enable the function handle to evaluate the solution at times outside of the original interval [0 1000].

  • Specify OutputVariables=1 so that the function handle interpolates only the first solution variable.

  • Specify two outputs to also return the integration results in the original interval.

[fh,S] = solutionFcn(F,0,1000,Extension="on",OutputVariables=1)
fh = function_handle with value:
    @ode.solutionFcn/interpolate


S = 
  ODEResults with properties:

        Time: [0 1.4606e-05 2.9212e-05 4.3818e-05 1.1010e-04 1.7639e-04 2.4267e-04 3.0896e-04 4.5006e-04 5.9116e-04 7.3226e-04 8.7336e-04 0.0010 0.0012 0.0013 0.0015 0.0017 0.0018 0.0021 0.0024 0.0027 0.0030 0.0033 0.0044 0.0055 ... ] (1x227 double)
    Solution: [2x227 double]

Extract and plot the integration results for the first solution variable in S, and then use the function handle fh to also evaluate the solution in the extended interval [1000 3000]. Plot the extended solution in red.

plot(S.Time,S.Solution(1,:),"-o")
t = linspace(1000,3000);
ys = fh(t);
hold on
plot(t,ys,"r-o")
hold off

Figure contains an axes object. The axes object contains 2 objects of type line.

Input Arguments

collapse all

ODE problem to solve, specified as an ode object.

Time limits for interpolation, specified as two scalars that define the range of acceptable values of t that you can use as inputs to fh for interpolation. The tmin and tmax arguments must satisfy tmin <= t0 <= tmax, where t0 is the value of F.InitialTime.

Example: fh = solutionFcn(F,0,10) returns a function handle fh that can interpolate F at any time in the range [0 10].

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: fh = solutionFcn(F,0,10,OutputVariables=[1 2],Extension="on")

Subset of variables for interpolation, specified as a scalar index or vector of indices. Use this option when the value returned by F.ODEFcn is a vector and you want to limit the number of variables that fh can interpolate. Specify one or more indices for the solution variables returned by F.ODEFcn that fh can interpolate.

The value of this option affects only the behavior of fh; it does not affect the solution returned in S. Use F.SolverOptions.OutputSelection to limit the number of output variables returned in S.

Example: fh = solutionFcn(F,0,5,OutputVariables=3) returns a function handle fh that interpolates the third solution component of F.

Example: fh = solutionFcn(F,0,5,OutputVariables=[1 3]) returns a function handle fh that interpolates the first and third solution components of F.

Time interval extension mode, specified as "on" or "off". Use this option to enable querying fh with time values outside of the solution interval [tmin tmax].

  • By default, Extension="off" and the command fh(t) returns NaN for values of t outside of the solution interval [tmin tmax].

  • If Extension="on", then you can query fh(t) with values of t outside of the solution interval [tmin tmax]. This requires the solver to run again to extend the solution domain, so there can be a performance difference between querying points inside or outside the solution interval.

Example: fh = solutionFcn(F,0,3,Extension="on") enables fh to be queried with time values outside of the interval [0 3].

Output Arguments

collapse all

Function for interpolation, returned as a function handle. fh uses the built-in interpolant for the solver, which enables efficient interpolation during intermediate steps of the integration. You can specify one or two outputs when you use fh:

  • y = fh(t) returns the computed solution at the times specified by t. The output y matches S.Solution if S = solve(F,t).

  • [y,dydt] = fh(t) also returns the interpolated derivative values dydt.

Computed solution, returned as an ODEResults object.

Version History

Introduced in R2023b

See Also

| | |