cyclebasis
Description
cycles = cyclebasis(G)cycles is a cell array
that indicates which nodes belong to each fundamental cycle.
[
also returns the edges in each cycle. The output cycles,edgecycles] = cyclebasis(G)edgecycles is a cell
array where edgecycles{k} gives the edges between the nodes in
cycles{k}.
Examples
Create and plot an undirected graph.
s = [1 1 2 2 3 4 4 5 5 6 7 8]; t = [2 4 3 5 6 5 7 6 8 9 8 9]; G = graph(s,t); plot(G)
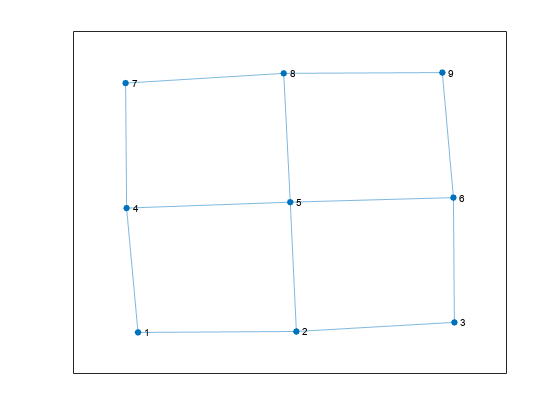
Calculate which nodes are in each fundamental cycle.
cycles = cyclebasis(G)
cycles=4×1 cell array
{[1 2 5 4]}
{[2 3 6 5]}
{[4 5 8 7]}
{[5 6 9 8]}
Compute the nodes and edges in the fundamental cycles of a graph, visualize the fundamental cycles, and then use the fundamental cycles to find other cycles in the graph.
Create and plot an undirected graph.
s = [1 1 1 2 2 3 3 4 4 4 5 6]; t = [2 3 4 4 5 4 6 5 6 7 7 7]; G = graph(s,t); plot(G);
Compute the fundamental cycle basis of the graph.
[cycles,edgecycles] = cyclebasis(G)
cycles=6×1 cell array
{[1 2 4]}
{[1 3 4]}
{[2 4 5]}
{[3 4 6]}
{[4 5 7]}
{[4 6 7]}
edgecycles=6×1 cell array
{[ 1 4 3]}
{[ 2 6 3]}
{[ 4 8 5]}
{[ 6 9 7]}
{[8 11 10]}
{[9 12 10]}
Highlight each of the fundamental cycles, using tiledlayout and nexttile to construct an array of subplots. For each subplot, first get the nodes of the corresponding cycle from cycles, and the edges from edgecycles. Then, plot the graph and highlight those nodes and edges.
tiledlayout flow for k = 1:length(cycles) nexttile highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r') title("Cycle " + k) end

You can construct any other cycle in the graph by finding the symmetric difference between two or more fundamental cycles using the setxor function. For example, take the symmetric difference between the first two cycles and plot the resulting new cycle.
figure
new_cycle_edges = setxor(edgecycles{1},edgecycles{2});
highlight(plot(G),'Edges',new_cycle_edges,'EdgeColor','r','NodeColor','r')
While every cycle can be constructed by combining cycles from the cycle basis, not every combination of basis cycles forms a valid cycle.
Examine how the outputs of the cyclebasis and allcycles functions scale with the number of edges in a graph.
Create and plot a square grid graph with three nodes on each side of the square.
n = 5; A = delsq(numgrid('S',n)); G = graph(A,'omitselfloops'); plot(G)

Compute all cycles in the graph using allcycles. Use the tiledlayout function to construct an array of subplots and highlight each cycle in a subplot. The results indicate there are a total of 13 cycles in the graph.
[cycles,edgecycles] = allcycles(G); tiledlayout flow for k = 1:length(cycles) nexttile highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r') title("Cycle " + k) end

Some of these cycles can be seen as combinations of smaller cycles. The cyclebasis function returns a subset of the cycles that form a basis for all other cycles in the graph. Use cyclebasis to compute the fundamental cycle basis and highlight each fundamental cycle in a subplot. Even though there are 13 cycles in the graph, there are only four fundamental cycles.
[cycles,edgecycles] = cyclebasis(G); tiledlayout flow for k = 1:length(cycles) nexttile highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r') title("Cycle " + k) end

Now, increase the number of nodes on each side of the square graph from three to four. This represents a small increase in the size of the graph.
n = 6; A = delsq(numgrid('S',n)); G = graph(A,'omitselfloops'); figure plot(G)

Use allcycles to compute all of the cycles in the new graph. For this graph there are over 200 cycles, which is too many to plot.
allcycles(G)
ans=213×1 cell array
{[ 1 2 3 4 8 7 6 5]}
{[ 1 2 3 4 8 7 6 10 9 5]}
{[1 2 3 4 8 7 6 10 11 12 16 15 14 13 9 5]}
{[ 1 2 3 4 8 7 6 10 11 15 14 13 9 5]}
{[ 1 2 3 4 8 7 6 10 14 13 9 5]}
{[ 1 2 3 4 8 7 11 10 6 5]}
{[ 1 2 3 4 8 7 11 10 9 5]}
{[ 1 2 3 4 8 7 11 10 14 13 9 5]}
{[ 1 2 3 4 8 7 11 12 16 15 14 10 6 5]}
{[ 1 2 3 4 8 7 11 12 16 15 14 10 9 5]}
{[ 1 2 3 4 8 7 11 12 16 15 14 13 9 5]}
{[1 2 3 4 8 7 11 12 16 15 14 13 9 10 6 5]}
{[ 1 2 3 4 8 7 11 15 14 10 6 5]}
{[ 1 2 3 4 8 7 11 15 14 10 9 5]}
{[ 1 2 3 4 8 7 11 15 14 13 9 5]}
{[ 1 2 3 4 8 7 11 15 14 13 9 10 6 5]}
⋮
Despite the large number of cycles in the graph, cyclebasis still returns a small number of fundamental cycles. Each of the cycles in the graph can be constructed using only nine fundamental cycles.
[cycles,edgecycles] = cyclebasis(G); figure tiledlayout flow for k = 1:length(cycles) nexttile highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r') title("Cycle " + k) end

The large increase in the number of cycles with only a small change in the size of the graph is typical for some graph structures. The number of cycles returned by allcycles can grow exponentially with the number of edges in the graph. However, the number of cycles returned by cyclebasis can, at most, grow linearly with the number of edges in the graph.
Input Arguments
Input graph, specified as a graph object. Use graph to create an undirected graph object.
Example: G = graph(1,2)
Output Arguments
Fundamental graph cycles, returned as a cell array. Each cell
cycles{k} contains the nodes that belong to one of the fundamental
cycles of G. Each cycle begins with the smallest node index. If
G does not contain any cycles, then cycles is
empty.
Every cycle in G is a combination of the fundamental cycles
returned in cycles. If an edge is part of a cycle in
G, then it is also part of at least one fundamental cycle in
cycles.
The data type of the cells in cycles depends on whether the input
graph contains node names:
If graph
Gdoes not have node names, then each cellcycles{k}is a numeric vector of node indices.If graph
Ghas node names, then each cellcycles{k}is a cell array of character vector node names.
Edges in each fundamental cycle, returned as a cell array. Each cell
edgecycles{k} contains the edge indices for edges in cycle
cycles{k}. If G does not contain any cycles,
then edgecycles is empty.
More About
A cycle exists in a graph when there is a nonempty path in which only the
first and last nodes are repeated. That is, aside from the first node being repeated
at the end of the path to close the cycle, no other nodes are repeated. An example
of a cycle is: (Node1 - Node2 - Node3 - Node1). By convention,
cyclebasis does not return the last node in the cycle
since it is the same as the first.
A cycle cannot traverse the same edge twice. For example, the cycle (Node1 - Node2 - Node1) in an undirected graph only exists if there is more than one edge connecting Node1 and Node2. By this definition, self-loops count as cycles, though they cannot be part of a larger cycle.
In undirected graphs, the fundamental cycle basis is a set of simple cycles that forms a basis for the cycle space of the graph. That is, any cycle in the graph can be constructed from the fundamental cycles. For an example, see Nodes and Edges in Fundamental Cycles.
The fundamental cycle basis of a graph is calculated from a minimum spanning tree of the graph. For each edge that is not in the minimum spanning tree, there exists one fundamental cycle which is composed of that edge, its end nodes, and the path in the minimum spanning tree that connects them.
The minimum spanning tree used in cyclebasis is generally different
from the one returned by minspantree. It is chosen such that the cycles
are short. However, cyclebasis is not guaranteed to return the shortest
possible fundamental cycle basis.
Version History
Introduced in R2021a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)