diag
Create diagonal matrix or get diagonal elements of matrix
Description
D = diag( returns
a square diagonal matrix with the elements of vector v)v on
the main diagonal.
Examples
Create a 1-by-5 vector.
v = [2 1 -1 -2 -5];
Use diag to create a matrix with the elements of v on the main diagonal.
D = diag(v)
D = 5×5
2 0 0 0 0
0 1 0 0 0
0 0 -1 0 0
0 0 0 -2 0
0 0 0 0 -5
Create a matrix with the elements of v on the first super diagonal (k=1).
D1 = diag(v,1)
D1 = 6×6
0 2 0 0 0 0
0 0 1 0 0 0
0 0 0 -1 0 0
0 0 0 0 -2 0
0 0 0 0 0 -5
0 0 0 0 0 0
The result is a 6-by-6 matrix. When you specify a vector of length n as an input, diag returns a square matrix of size n+abs(k).
Get the elements on the main diagonal of a random 6-by-6 matrix.
A = randi(10,6)
A = 6×6
9 3 10 8 7 8
10 6 5 10 8 1
2 10 9 7 8 3
10 10 2 1 4 1
7 2 5 9 7 1
1 10 10 10 2 9
x = diag(A)
x = 6×1
9
6
9
1
7
9
Get the elements on the first subdiagonal (k=-1) of A. The result has one fewer element than the main diagonal.
x1 = diag(A,-1)
x1 = 5×1
10
10
2
9
2
Calling diag twice returns a diagonal matrix composed of the diagonal elements of the original matrix.
A1 = diag(diag(A))
A1 = 6×6
9 0 0 0 0 0
0 6 0 0 0 0
0 0 9 0 0 0
0 0 0 1 0 0
0 0 0 0 7 0
0 0 0 0 0 9
Input Arguments
Diagonal elements, specified as a vector. If v is
a vector with N elements, then diag(v,k) is
a square matrix of order N+abs(k).
diag([]) returns an empty matrix, [].
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char
Complex Number Support: Yes
Input matrix. diag returns an error if ndims(A)
> 2.
diag([]) returns an empty matrix, [].
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char
Complex Number Support: Yes
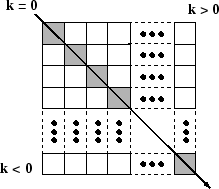
Diagonal number, specified as an integer. k=0 represents
the main diagonal, k>0 is above the main diagonal,
and k<0 is below the main diagonal.
For an m-by-n matrix, k is in the
range . For example, for matrices with n greater than
m, the k=0 main diagonal consists of the elements with
indices (1,1), (2,2), ..., (m,m).
The k=1 above the main diagonal consists of the elements with indices
(1,2), (2,3), ..., (m,m+1). The
k=-1 below the main diagonal consists of the elements with indices
(2,1), (3,2), ..., (m,m-1).
Tips
The
traceof a matrix is equal tosum(diag(A)).
Extended Capabilities
Usage notes and limitations:
If you supply
k, then it must be a real and scalar integer value.For variable-size inputs that are variable-length vectors (1-by-: or :-by-1),
diag:Treats the input as a vector
Returns a matrix with the input vector along the specified diagonal
For variable-size inputs that are not variable-length vectors,
diag:Treats the input as a matrix
Does not support inputs that are vectors at run time
Returns a variable-length vector
If the input is variable-size (:m-by-:n) and has shape 0-by-0 at run time, then the output is 0-by-1, not 0-by-0. However, if the input is a constant size 0-by-0, then the output is
[].For variable-size inputs that are not variable-length vectors (1-by-: or :-by-1),
diagtreats the input as a matrix from which to extract a diagonal vector. This behavior occurs even if the input array is a vector at run time. To forcediagto build a matrix from variable-size inputs that are not 1-by-: or :-by-1, use:diag(x(:))instead ofdiag(x)diag(x(:),k)instead ofdiag(x,k)
Usage notes and limitations:
If you supply
k, then it must be a real and scalar integer value.For variable-size inputs that are variable-length vectors (1-by-: or :-by-1),
diag:Treats the input as a vector
Returns a matrix with the input vector along the specified diagonal
For variable-size inputs that are not variable-length vectors,
diag:Treats the input as a matrix
Does not support inputs that are vectors at run time
Returns a variable-length vector
If the input is variable-size (:m-by-:n) and has shape 0-by-0 at run time, then the output is 0-by-1, not 0-by-0. However, if the input is a constant size 0-by-0, then the output is
[].For variable-size inputs that are not variable-length vectors (1-by-: or :-by-1),
diagtreats the input as a matrix from which to extract a diagonal vector. This behavior occurs even if the input array is a vector at run time. To forcediagto build a matrix from variable-size inputs that are not 1-by-: or :-by-1, use:diag(x(:))instead ofdiag(x)diag(x(:),k)instead ofdiag(x,k)
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
The diag function
fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)