Propagation Channel Models
LTE Toolbox™ provides a set of channel models that enable you to test and verify UE and eNodeB radio transmission and reception as defined in TS 36.101 [1] and TS 36.104 [2]. The following channel models are available in LTE Toolbox.
Multipath fading propagation conditions
High speed train conditions
Moving propagation conditions
Multipath Fading Propagation Conditions
The multipath fading channel model specifies the following three delay profiles.
Extended Pedestrian A model (EPA)
Extended Vehicular A model (EVA)
Extended Typical Urban model (ETU)
These three delay profiles represent a low, medium, and high delay spread environment, respectively. The multipath delay profiles for these channels are shown in these tables.
EPA Delay Profile
| Excess tap delay (ns) | Relative power (dB) |
|---|---|
| 0 | 0.0 |
| 30 | –1.0 |
| 70 | –2.0 |
| 90 | –3.0 |
| 110 | –8.0 |
| 190 | –17.2 |
| 410 | –20.8 |
EVA Delay Profile
| Excess tap delay (ns) | Relative power (dB) |
|---|---|
| 0 | 0.0 |
| 30 | –1.5 |
| 150 | –1.4 |
| 310 | –3.6 |
| 370 | –0.6 |
| 710 | –9.1 |
| 1090 | –7.0 |
| 1730 | –12.0 |
| 2510 | –16.9 |
ETU Delay Profile
| Excess tap delay (ns) | Relative power (dB) |
|---|---|
| 0 | –1.0 |
| 50 | –1.0 |
| 120 | –1.0 |
| 200 | 0.0 |
| 230 | 0.0 |
| 500 | 0.0 |
| 1600 | –3.0 |
| 2300 | –5.0 |
| 5000 | –7.0 |
All the taps in the preceding tables have a classical Doppler spectrum. In addition to a multipath delay profile, each multipath fading propagation condition has a maximum Doppler frequency as shown in this table.
| Channel model | Maximum Doppler frequency |
|---|---|
| EPA 5Hz | 5 Hz |
| EVA 5Hz | 5 Hz |
| EVA 70Hz | 70 Hz |
| ETU 70Hz | 70 Hz |
| ETU 300Hz | 300 Hz |
In the case of MIMO environments, a set of correlation matrices model the correlation between UE and eNodeB antennas. These correlation matrices are described in MIMO Channel Correlation Matrices.
High Speed Train Condition
The high speed train condition defines a non-fading propagation channel with single multipath component, the position of which is fixed in time. This single multipath represents the Doppler shift, which is caused by a high speed train moving past a base station, as shown in the following figure.

The expression is the initial distance of the train from eNodeB, and is the minimum distance between eNodeB and the railway track. Both variables are measured in meters. The variable ν is the velocity of the train in meters per second. The Doppler shift due to a moving train is given in the following equation.
The variable is the Doppler shift and is the maximum Doppler frequency. The cosine of angle is given by the following equation.
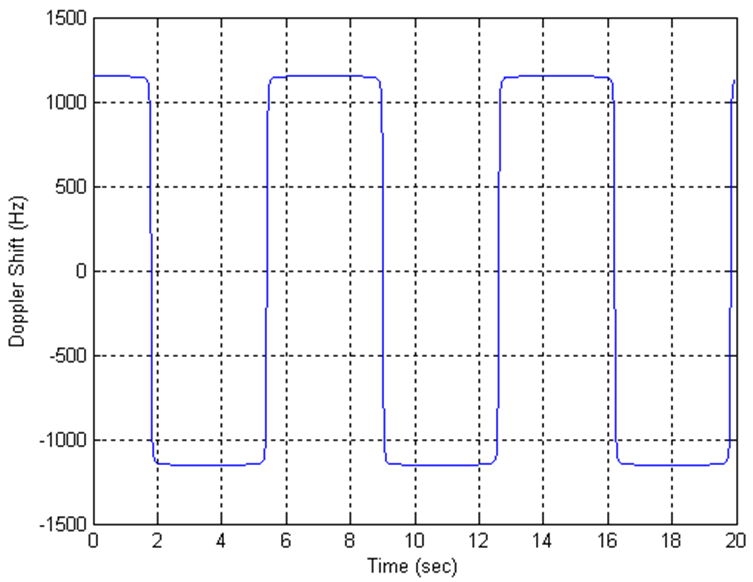
For eNodeB testing, two high speed train scenarios use the parameters listed in the following table. You can calculate the Doppler shift using the preceding equations with the parameters listed in this table.
| Parameter | Value | |
|---|---|---|
| Scenario 1 | Scenario 3 | |
| 1,000 m | 300 m | |
| 50 m | 2 m | |
| ν | 350 km/hr | 300 km/kr |
| 1,340 Hz | 1,150 Hz | |
Both of these scenarios result in Doppler shifts that apply to all frequency bands. The Doppler shift trajectory for scenario 1 is shown in this figure.

The Doppler shift trajectory for scenario 3 is shown in the following figure.
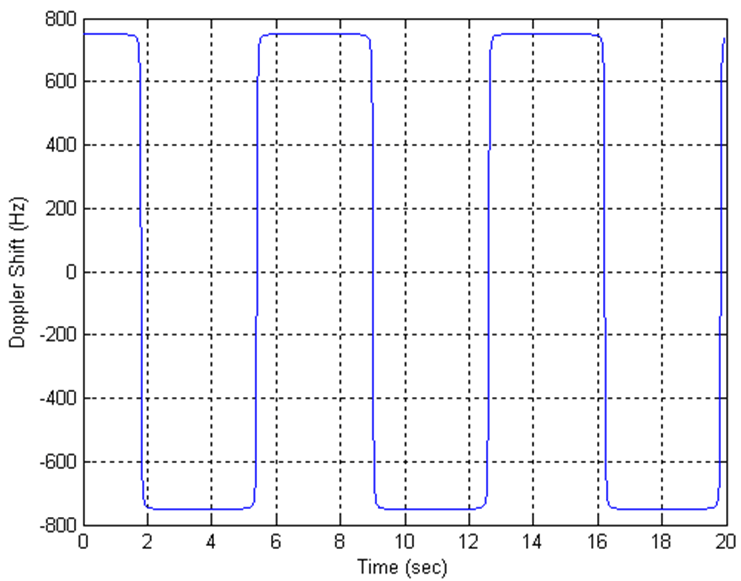
For UE testing, you can calculate the Doppler shift using the preceding equations with the parameters listed in this table.
| Parameter | Value |
|---|---|
| 300 m | |
| 2 m | |
| ν | 300 km/hr |
| 750 Hz |
These parameters result in the Doppler shift, applied to all frequency bands, shown in this figure.
Moving Propagation Condition
The moving propagation channel in LTE defines a channel condition where the location of multipath components changes. The time difference between the reference time and the first tap, Δτ, is given by the following equation.
The variable A is the starting time in seconds and Δω is angular rotation in radians per second.
Note
Relative time between multipath components stays fixed.
The parameters for the moving propagation conditions are shown in this table.
| Parameter | Scenario 1 | Scenario 2 |
|---|---|---|
| Channel model | ETU200 | AWGN |
| UE speed | 120 km/hr | 350 km/hr |
| CP length | Normal | Normal |
| A | 10 μs | 10 μs |
| Δω | 0.04 s–1 | 0.13 s–1 |
Doppler shift applies only for generating fading samples for scenario 1. Scenario 2 models a single non-fading multipath component with additive white gaussian noise (AWGN). The location of this multipath component changes with time according to the preceding equation.
An example of a moving channel with a single non-fading tap is shown in this figure.

MIMO Channel Correlation Matrices
In MIMO systems, there is correlation between transmit and receive antennas. This depends on multiple factors such as the separation between antenna and the carrier frequency. For maximum capacity, it is desirable to minimize the correlation between transmit and receive antennas.
There are different ways to model antenna correlation. One technique uses correlation matrices to describe the correlation between multiple antennas both at the transmitter and the receiver. The technique is to compute the matrices independently at both the transmitter and the receiver, then combine them using the Kronecker product to generate a channel spatial correlation matrix.
TS 36.101 [1] defines three different correlation levels.
low or no correlation
medium correlation
high correlation
For each level of correlation, there exist parameters α and β as shown in this table.
| Low correlation | Medium correlation | High correlation | |||
|---|---|---|---|---|---|
| α | β | α | β | α | β |
| 0 | 0 | 0.3 | 0.9 | 0.9 | 0.9 |
The independent correlation matrices at eNodeB and UE, which are denoted by ReNB and RUE respectively, are shown for different amounts of antennas (one, two, and four) in this table.
| Correlation | One antenna | Two antennas | Four antennas |
|---|---|---|---|
| eNodeB | |||
| UE |
The channel spatial correlation matrix, Rspat, is given by the following equation.
The symbol ⊗ represents the Kronecker product. The values of the channel spatial correlation matrix Rspat, for different matrix sizes are defined in this table.
| Matrix size | Rspat values |
|---|---|
| 1×2 case | |
| 2×2 case | |
| 4×2 case | |
| 4×4 case |
References
[1] 3GPP TS 36.101. “Evolved Universal Terrestrial Radio Access (E-UTRA); User Equipment (UE) Radio Transmission and Reception.” 3rd Generation Partnership Project; Technical Specification Group Radio Access Network. URL: https://www.3gpp.org.
[2] 3GPP TS 36.104. “Evolved Universal Terrestrial Radio Access (E-UTRA); Base Station (BS) Radio Transmission and Reception.” 3rd Generation Partnership Project; Technical Specification Group Radio Access Network. URL: https://www.3gpp.org.
See Also
lteFadingChannel | lteHSTChannel | lteMovingChannel