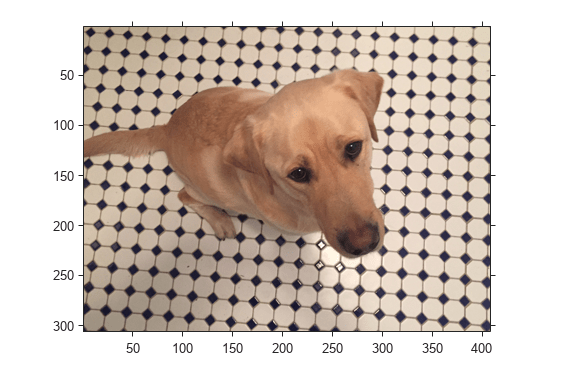
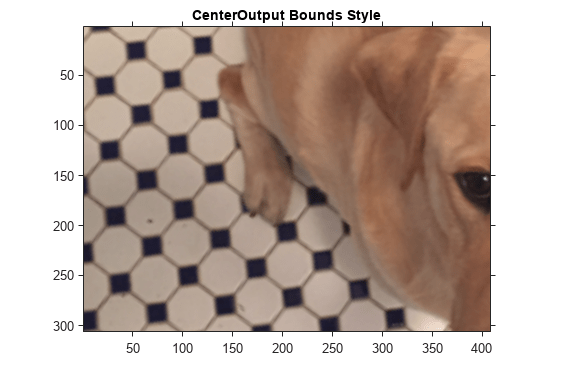
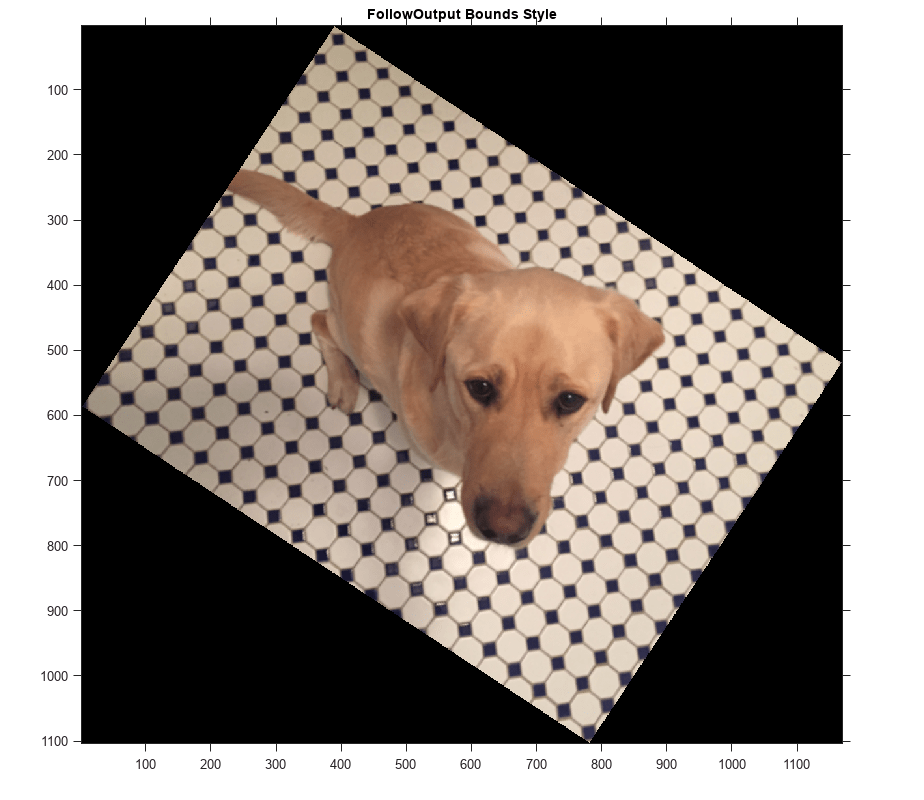
imwarp
Apply geometric transformation to image
Syntax
Description
[___] = imwarp(___,
specifies the type of interpolation to use.interp)
[___] =
imwarp(___,
specifies name-value arguments to control various aspects of the geometric
transformation. Name=Value)
Tip
If the input transformation tform does not define a
forward transform, then use the OutputView name-value
argument to accelerate the transformation.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
If you want to apply an identical geometric transformation to a batch of same-sized images, consider using the
Warperobject and thewarpfunction. Compared toimwarp, theWarperobject speeds up the transformation significantly for batches of small to medium-sized images, with diminishing returns for larger images.
Algorithms
imwarp determines the value of pixels in the
output image by mapping locations in the output image to the corresponding locations in
the input image (an inverse mapping). When the center of a pixel in the output image
does not map to the center of a pixel in the input image, imwarp
interpolates within the input image to calculate the output pixel value.
The figure illustrates a translation transformation of a checkerboard image, in which each square is 10-by-10 pixels. By convention, the axes in input space are labeled u and v and the axes in output space are labeled x and y. Using the inverse transformation, the pixel with (x,y) coordinates (25,35) in the output coordinate space is mapped to the (u,v) coordinates (5,5) in the input coordinate space.
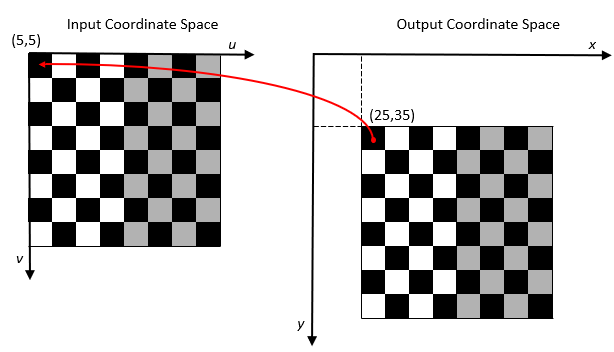
imwarp performs the mapping using world coordinates. For more
information, see Image Coordinate Systems.