Estimate Nonlinear ARX Models at the Command Line
You can estimate nonlinear ARX models after you perform the following tasks:
Prepare your data, as described in Preparing Data for Nonlinear Identification.
(Optional) Estimate model orders and delays the same way you would for linear ARX models. See Preliminary Step – Estimating Model Orders and Input Delays.
(Optional) Choose a mapping function for the output function in Available Mapping Functions for Nonlinear ARX Models.
(Optional) Estimate or construct a linear ARX model for initialization of nonlinear ARX model. See Initialize Nonlinear ARX Estimation Using Linear Model.
Estimate Model Using nlarx
Use nlarx to both construct
and estimate a nonlinear ARX model. After each estimation, validate
the model by comparing it to other models and simulating or
predicting the model response.
Basic Estimation
Start with the simplest estimation using m = nlarx(data,[na nb nk]). For example:
load iddata1; % na = nb = 2 and nk = 1 m = nlarx(z1,[2 2 1])
m = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Wavelet network with 1 units Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 68.83% (prediction focus) FPE: 1.975, MSE: 1.885 Model Properties
View the regressors.
getreg(m)
ans = 4×1 cell
{'y1(t-1)'}
{'y1(t-2)'}
{'u1(t-1)'}
{'u1(t-2)'}
The second input argument [na nb nk] specifies the model orders and delays.
By default, the output function is the wavelet network idWaveletNetwork, which accepts
regressors as inputs to its linear and nonlinear functions. m is
an idnlarx object.
For MIMO systems, nb, nf,
and nk are ny-by-nu matrices.
See the nlarx reference page for more information
about MIMO estimation.
Specify a different mapping function (for example, sigmoid network).
M = nlarx(z1,[2 2 1],'idSigmoidNetwork');Create an nlarxOptions option set and configure the Focus property to minimize simulation error.
opt = nlarxOptions('Focus','simulation'); M = nlarx(z1,[2 2 1],'idSigmoidNetwork',opt);
Configure Model Regressors
Linear Regressors
Linear regressors represent linear functions that are based on delayed input and
output variables and which provide the inputs into the model output function. When
you use orders to specify a model, the number of input regressors is equal to
na and the number of output regressors is equal to
nb. The orders syntax limits you to consecutive lags. You can
also create linear regressors using linearRegressor. When you use linearRegressor, you
can specify arbitrary lags.
For example, estimate a nonlinear ARX model using model orders to specify linear regressors. Display the regressors using getreg.
load iddata1
m = nlarx(z1,[2 2 1],idSigmoidNetwork);
getreg(m);The model stores the regressor specification in the property m.Regressors. Create an additional linear regressor set L that contains regressors 'y1(t-3)' and 'y1(t-5)'. Append L to the model regressors.
L = linearRegressor({'y1'},{[3 5]});
m.Regressors = [m.Regressors;L];
getreg(m)ans = 6×1 cell
{'y1(t-1)'}
{'y1(t-2)'}
{'u1(t-1)'}
{'u1(t-2)'}
{'y1(t-3)'}
{'y1(t-5)'}
The model now contains six linear regressors.
Polynomial Regressors
Explore including polynomial regressors using polynomialRegressor in addition to the linear regressors in the
nonlinear ARX model structure. Polynomial regressors are polynomial functions of
delayed inputs and outputs. (see Nonlinear ARX Model Orders and Delay).
For example, generate polynomial regressors up to order 2.
P = polynomialRegressor({'y1','u1'},{[1],[2]},2);Append the polynomial regressors to the linear regressors in m.Regressors.
m.Regressors = [m.Regressors;P]; getreg(m)
ans = 8×1 cell
{'y1(t-1)' }
{'y1(t-2)' }
{'u1(t-1)' }
{'u1(t-2)' }
{'y1(t-3)' }
{'y1(t-5)' }
{'y1(t-1)^2'}
{'u1(t-2)^2'}
m now includes polynomial regressors.
View the size of the m.Regressors array.
size(m.Regressors)
ans = 1×2
3 1
The array now contains three regressor objects.
Custom Regressors
Use customRegressor to construct regressors
as arbitrary functions of model input and output variables.
For example, create two custom regressors that implement 'sin(y1(t-1)' and 'y1(t-2).*u1(t-3)'.
C1 = customRegressor({'y1'},{1},@(x)sin(x));
C2 = customRegressor({'y1','u1'},{2,3},@(x,y)x.*y);
m.Regressors = [m.Regressors;C1;C2];
getreg(m) % displays all regressorsans = 10×1 cell
{'y1(t-1)' }
{'y1(t-2)' }
{'u1(t-1)' }
{'u1(t-2)' }
{'y1(t-3)' }
{'y1(t-5)' }
{'y1(t-1)^2' }
{'u1(t-2)^2' }
{'sin(y1(t-1))' }
{'y1(t-2).*u1(t-3)'}
View the properties of custom regressors. For example, get the function handle of the first custom regressor in the array. This regressor is the fourth regressor set in the Regressors array.
C1_fcn = m.Regressors(4).VariablesToRegressorFcn
C1_fcn = function_handle with value:
@(x)sin(x)
View the regressor description.
display(m.Regressors(4))
Custom regressor: sin(y1(t-1))
VariablesToRegressorFcn: @(x)sin(x)
Variables: {'y1'}
Lags: {[1]}
Vectorized: 1
TimeVariable: 't'
Regressors described by this set
Combine Regressors
Once you have created linear, polynomial, and custom regressor objects, you can combine them in any way you want to suit your estimation needs.
You can exclude all linear regressors and use only polynomial and custom regressors when you estimate the model.
Create a new regressor set that contains only the polynomial and custom regressors.
R = [P;C1;C2]; m = nlarx(z1,R,idLinear)
m = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: 1. Order 2 regressors in variables y1, u1 2. Custom regressor: sin(y1(t-1)) 3. Custom regressor: y1(t-2).*u1(t-3) List of all regressors Output function: Linear with offset Sample time: 0.1 seconds Status: Estimated using NLARX on time domain data "z1". Fit to estimation data: 0.4112% (prediction focus) FPE: 19.97, MSE: 19.24 Model Properties
In advanced applications, you can specify the advanced estimation option for mapping objects of the output function. For example, idWaveletNetwork and idTreepartition objects provide the Options property for setting such estimation options.
Specify Regressor Inputs to Linear and Nonlinear Components
Model regressors can enter as inputs to either or both linear and nonlinear function components of the mapping functions making up the output function. To reduce model complexity and keep the estimation well-conditioned, consider assigning a reduced set of regressors to the nonlinear component. You can also assign a subset of regressors to the linear component. The regressor usage table that manages the assignments provides complete flexibility. You can assign any combination of regressors to each component. For example, specify a nonlinear ARX model to be linear in past outputs and nonlinear in past inputs.
m = nlarx(z1,[2 2 1]); disp(m.RegressorUsage)
y1:LinearFcn y1:NonlinearFcn
____________ _______________
y1(t-1) true true
y1(t-2) true true
u1(t-1) true true
u1(t-2) true true
m.RegressorUsage{3:4,1} = false;
m.RegressorUsage{1:2,2} = false;
disp(m.RegressorUsage) y1:LinearFcn y1:NonlinearFcn
____________ _______________
y1(t-1) true false
y1(t-2) true false
u1(t-1) false true
u1(t-2) false true
Configure Output Function
Specify the mapping function object of the output function directly in the estimation command as:
A character vector of the mapping function name. This syntax uses the default configuration of the mapping function.
m = nlarx(z1, [2 2 1],idSigmoidNetwork);
A mapping function object. This syntax allows you to modify the function configuration.
m = nlarx(z1,[2 2 1],idWaveletNetwork(5));
This estimation uses a nonlinear ARX model with an idWaveletNetwork mapping function that has 5 units. To construct the mapping object before providing it as an input to nlarx, use one of the following command sequences.
w = idWaveletNetwork(5);
m = nlarx(z1,[2 2 1],w);
% or
w = idWaveletNetwork;
w.NonlinearFcn.NumberOfUnits = 5;
m = nlarx(z1,[2 2 1],w);For MIMO systems, you can specify a different mapping function for each output. For example, to specify idSigmoidNetwork for the first output and idWaveletNetwork for the second output:
load iddata1 z1 load iddata2 z2 data = [z1, z2(1:300)]; M = nlarx(data,[[1 1;1 1] [2 1;1 1] [2 1;1 1]],[idSigmoidNetwork; idWaveletNetwork]);
If you want the same nonlinearity for all output channels, specify one nonlinearity.
M = nlarx(data,[[1 1;1 1] [2 1;1 1] [2 1;1 1]],idSigmoidNetwork);
The following table summarizes available mapping objects for the model output function.
| Mapping Description | Value (Default Mapping Object Configuration) | Mapping Object |
|---|---|---|
| Wavelet network (default) | 'idWaveletNetwork' or 'wave' | idWaveletNetwork |
| One layer sigmoid network | 'idSigmoidNetwork' or 'sigm' | idSigmoidNetwork |
| Tree partition | 'idTreePartition' or 'tree' | idTreePartition |
| F is linear in x | 'idLinear' or [ ] or '' | idLinear |
| Neural Network | 'idNeuralNetwork' | idNeuralNetwork |
You can also specify a custom network. For example, specify a custom network by defining a
function called gaussunit.m, as described in the idCustomNetwork reference page. Define
the custom network object CNetw and estimate the model:
CNetw = idCustomNetwork(@gaussunit); m = nlarx(data,[na nb nk],CNetw)
Exclude Linear Function in Output Function
If your model output function includes idWaveletNetwork, idSigmoidNetwork, or idCustomNetwork mapping objects,
you can exclude the linear function using the LinearFcn.Use
property of the mapping object. The mapping object becomes
F(x)=, where g(.) is the nonlinear function and
y0 is the offset.
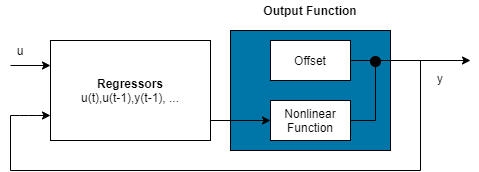
For example:
SMO = idSigmoidNetwork; SMO.LinearFcn.Use = false; m = nlarx(z1,[2 2 1],SMO);
Note
You cannot exclude the linear function from tree partition and neural network mapping objects.
Exclude Nonlinear Function in Output Function
Configure the nonlinear ARX structure to include only the linear function in
the mapping object by setting the mapping object to idLinear. In this case, is a weighted sum of model regressors plus an offset. Such
models provide a bridge between purely linear ARX models and fully flexible
nonlinear models.
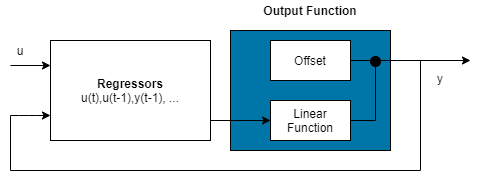
In the simplest case, a model with only linear regressors is linear (affine). For example, this structure:
m = nlarx(z1,[2 2 1],idLinear);
is similar to the linear ARX model:
lin_m = arx(z1,[2 2 1]);
However, the nonlinear ARX model m is more flexible than the linear ARX model lin_m because it contains the offset term, d. This offset term provides the additional flexibility of capturing signal offsets, which is not available in linear models.
A popular nonlinear ARX configuration in many applications uses polynomial
regressors to model system nonlinearities. In such cases, the system is
considered to be a linear combination of products of (delayed) input and output
variables. Use the polynomialRegressor command to easily
generate combinations of regressor products and powers.
For example, suppose that you know the output y(t) of a system to be a linear combination of (y(t − 1))2, (u(t − 1))2 and y(t − 1)u(t − 1)). To model such a system, use:
P = polynomialRegressor({'y1','u1'},{1,1},2)P =
Order 2 regressors in variables y1, u1
Order: 2
Variables: {'y1' 'u1'}
Lags: {[1] [1]}
UseAbsolute: [0 0]
AllowVariableMix: 0
AllowLagMix: 0
TimeVariable: 't'
Regressors described by this set
P.AllowVariableMix = true; M = nlarx(z1,P,idLinear); getreg(M)
ans = 3×1 cell
{'y1(t-1)^2' }
{'u1(t-1)^2' }
{'y1(t-1)*u1(t-1)'}
For more complex combinations of polynomial delays and mixed-variable regressors, you can also use customRegressor.
Iteratively Refine Model
If your model structure includes mapping objects that support iterative search (see Specify Estimation Options for Nonlinear ARX Models), you can use nlarx to refine model parameters:
m1 = nlarx(z1,[2 2 1],idSigmoidNetwork);
m2 = nlarx(z1,m1); % can repeatedly run this commandYou can also use pem to refine the original model:
m2 = pem(z1,m1);
Check the search termination criterion m.Report.Termination.WhyStop. If WhyStop indicates that the estimation reached the maximum number of iterations, try repeating the estimation and possibly specifying a larger value for the nlarxOptions.SearchOptions.MaxIterations estimation option:
opt = nlarxOptions; opt.SearchOptions.MaxIterations = 30; m2 = nlarx(z1,m1,opt); % runs 30 more iterations % starting from m1
When the m.Report.Termination.WhyStop value is Near (local) minimum, (norm( g) < tol or No improvement along the search direction with line search, validate your model to see if this model adequately fits the data. If not, the solution might be stuck in a local minimum of the cost-function surface. Try adjusting the SearchOptions.Tolerance value or the SearchMethod option in the nlarxOptions option set, and repeat the estimation.
You can also try perturbing the parameters of the last model using init (called
randomization) and refining the model using
nlarx:
M1 = nlarx(z1, [2 2 1], idSigmoidNetwork); % original model M1p = init(M1); % randomly perturbs parameters about nominal values M2 = nlarx(z1, M1p); % estimates parameters of perturbed model
You can display the progress of the iterative search in the MATLAB® Command Window using the nlarxOptions.Display estimation option:
opt = nlarxOptions('Display','on'); M2= nlarx(z1,M1p,opt);
Troubleshoot Estimation
If you do not get a satisfactory model after many trials with various model structures and algorithm settings, it is possible that the data is poor. For example, your data might be missing important input or output variables and does not sufficiently cover all the operating points of the system.
Nonlinear black-box system identification usually requires more data than linear model identification to gain enough information about the system.
Use nlarx to Estimate Nonlinear ARX Models
This example shows how to use nlarx to estimate a nonlinear ARX model for measured input/output data.
Prepare the data for estimation.
load twotankdata
z = iddata(y, u, 0.2);
ze = z(1:1000); zv = z(1001:3000);Estimate several models using different model orders, delays, and nonlinearity settings.
m1 = nlarx(ze,[2 2 1]); m2 = nlarx(ze,[2 2 3]); m3 = nlarx(ze,[2 2 3],idWaveletNetwork(8));
An alternative way to perform the estimation is to configure the model structure first, and then to estimate this model.
m4 = idnlarx([2 2 3],idSigmoidNetwork(14));
m4.RegressorUsage.("y1:NonlinearFcn")(3:4) = false;
m4 = nlarx(ze,m4);Compare the resulting models by plotting the model outputs with the measured output.
compare(zv, m1,m2,m3,m4)
