Tandem Primary Cylinder
This example shows how to model, parameterize and test a tandem primary cylinder starting from manufacturer datasheet information. First, there is a brief discussion on the mathematical modeling of the system. Given the numerical data extracted from the datasheet, optimization is then used to determine remaining unknown parameters. The model is then simulated and the resulting push rod force - brake pressure relationship curve is compared with the curve provided on the manufacturer datasheet. Understanding the behavior of the tandem primary cylinder is an important prerequisite to selection of other braking system components.
Model
The following figure shows the tandem primary cylinder test harness. Spring-loaded accumulators are used for loading in the 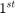 and the
and the  circuits in place of disk or drum brakes. The input to the model is the push rod force coming from the lever mechanism or the brake booster. Output of the model is the pressures achieved in the brake circuits 1 and 2 respectively.
circuits in place of disk or drum brakes. The input to the model is the push rod force coming from the lever mechanism or the brake booster. Output of the model is the pressures achieved in the brake circuits 1 and 2 respectively.

Manufacturer Datasheet Data
The supplier has provided the following data in the datasheet.
dp : first and second circuit piston diameter.
stroke1 : first circuit piston stroke.
stroke2 : second circuit piston stroke.
totalStroke : overall stroke.
disp1 : first circuit displacement.
disp2 : second circuit displacement.
totalDisp : net displacement.
maxPress : max pressure.
Pressure Development Characteristics
The supplier datasheet gives the following function diagram or the push rod force-brake pressure curve for the tandem primary cylinder.

Equations of Motion (EoM) of System
The following figure shows the tandem primary cylinder. Mass 1 and mass 2 use the coordinate frames shown below. This description only includes the mechanical EoM of the system. The fluid dynamics equations are not shown.

 , when
, when 
 , when
, when 
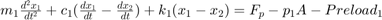 , when
, when 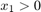
 , when
, when 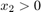
where,
 and
and  are positions of piston mass 1 and mass 2 from the left side assumed hard stop.
are positions of piston mass 1 and mass 2 from the left side assumed hard stop.
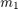 and
and  are masses of piston 1 and 2 respectively.
are masses of piston 1 and 2 respectively.
 and
and  are damping coefficients of piston 1 and 2 respectively.
are damping coefficients of piston 1 and 2 respectively.
 and
and  are stiffness coefficients of left (Spring 1) and right (spring 2) respectively.
are stiffness coefficients of left (Spring 1) and right (spring 2) respectively.
 is force applied on push rod of primary cylinder.
is force applied on push rod of primary cylinder.
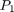 and
and  are pressures in brake circuit 1 and 2 respectively.
are pressures in brake circuit 1 and 2 respectively.
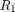 and
and 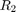 are reaction forces on mass 1 and 2 respectively when both masses are at the leftmost position.
are reaction forces on mass 1 and 2 respectively when both masses are at the leftmost position.
 and
and  are preloads on left and right side springs respectively.
are preloads on left and right side springs respectively.
Parameter Estimation Method
Some parameters, which are important for functionality assessment, are not provided in the manufacturer's datasheet, therefore to simulate the model it is pertinent to estimate these parameters. The EoM are converted to steady state equations to estimate unknown parameters.
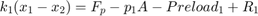 , when
, when 
 , when
, when 
 , when
, when 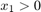
 , when
, when 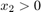
Data for the function diagram is explained with following figure.

where,
 and
and 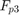 are the push rod forces for points 1,2, and 3 respectively.
are the push rod forces for points 1,2, and 3 respectively.
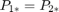 ,Here
,Here  is
is 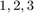 for the brake circuit pressures at points 1,2, and 3 respectively.
for the brake circuit pressures at points 1,2, and 3 respectively.
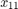 and
and 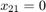 represent the leftmost positions for piston 1 and 2 respectively.
represent the leftmost positions for piston 1 and 2 respectively.
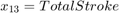 and
and  as per the manufacturer datasheet data.
as per the manufacturer datasheet data.
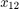 and
and  are piston positions at data point 2. This point needs to be iterated on during optimization to estimate the unknown parameters.
are piston positions at data point 2. This point needs to be iterated on during optimization to estimate the unknown parameters.
The estimation scheme is as follows:

The estimation should yield results with the following conditions met:
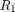 and
and 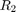 should be greater than or equal to 0.
should be greater than or equal to 0. and
and  should be greater than 0.
should be greater than 0.
Assumed Parameters
Some parameters are assumed as they are neither given in the datasheet nor can they be estimated. The following is the list:
c1 is damping coefficient for piston 1.
c2 is damping coefficient for piston 2.
mass1 is piston 1 mass.
mass2 is piston 2 mass.
v2D is brake circuit 1 dead volume.
v2M is brake circuit 1 maximum volume.
v4D is brake circuit 2 dead volume.
v4M is brake circuit 2 maximum volume.
a1Ori is compensating orifice area.
a2Ori is brake circuit orifice area
Load Circuit
It is important to test the system with the correct load. In the test model, loading is done on the tandem primary cylinder using spring-based accumulators. Setting up correct parameters in the accumulators is important. From the datasheet it is known what should be the stroke values for brake circuits 1 and 2 respectively. Iterated parameters 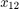 and
and  are important for deciding the fluid chamber capacity of the accumulators. Assumed or estimated parameters for the load circuit accumulators are:
are important for deciding the fluid chamber capacity of the accumulators. Assumed or estimated parameters for the load circuit accumulators are:
vol1 is fluid chamber capacity for brake circuit 1.
vol2 is fluid chamber capacity for brake circuit 2.
loadP1 is pressure at full capacity for brake circuit 1.
loadP2 is pressure at full capacity for brake circuit 2.
Simulation Results from Simscape Logging
The model generates push rod force-brake pressure plots for selected manufacturer designs. The applied push rod force to the tandem primary cylinder is ramped at a 25 N/sec rate in the simulation.
