fixed.interp1
Syntax
Description
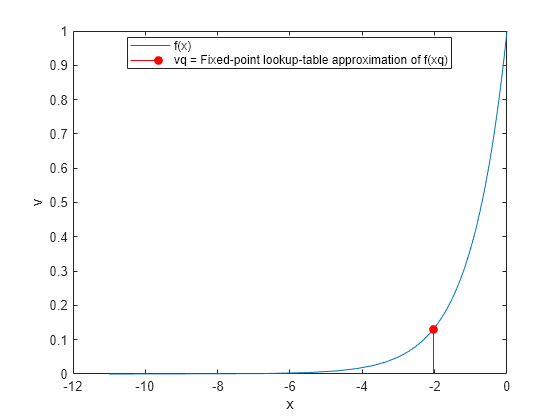
vq = fixed.interp1(x,v,xq)x contains the coordinates of the sample points
and v contains the corresponding function values at each sample point.
The variable xq contains the coordinates of the query points.
If you have multiple sets of data that are sampled at the same point coordinates, then
you can pass v as an array. Each column of array v
contains a different set of 1-D sample values.
vq = fixed.interp1(v,xq)1 to
n, where n depends on the shape of
v:
When v is a vector, the default points are
1:length(v).When v is an array, the default points are
1:size(v,1).
Use this syntax when you are not concerned about the absolute distances between points.
Examples
Input Arguments
Output Arguments
Extended Capabilities
Version History
Introduced in R2024a