PortfolioCVaR
Creates PortfolioCVaR object for conditional value-at-risk portfolio optimization and analysis
Description
Use PortfolioCVaR to create a
PortfolioCVaR object for conditional value-at-risk portfolio
optimization.
The main workflow for CVaR portfolio optimization is to create an instance of a
PortfolioCVaR object that completely specifies a portfolio
optimization problem and to operate on the PortfolioCVaR object using
supported functions to obtain and analyze efficient portfolios. For details on this
workflow, see PortfolioCVaR Object Workflow.
You can use the PortfolioCVaR object in several ways. To set up a
portfolio optimization problem in a PortfolioCVaR object, the
simplest syntax
is:
p = PortfolioCVaR;
PortfolioCVaR object, p, such
that all object properties are empty. The PortfolioCVaR object also accepts collections of name-value
pair arguments for properties and their values. The PortfolioCVaR
function accepts inputs for properties with the general
syntax:
p = PortfolioCVaR('property1',value1,'property2',value2, ... );If a PortfolioCVaR object already exists, the syntax permits the
first (and only the first argument) of the PortfolioCVaR object to be
an existing object with subsequent name-value pair arguments for properties to be added
or modified. For example, given an existing PortfolioCVaR object in
p, the general syntax
is:
p = PortfolioCVaR(p,'property1',value1,'property2',value2, ... );
Input argument names are not case sensitive, but must be completely specified. In
addition, several properties can be specified with alternative argument names (see Shortcuts for Property Names). The
PortfolioCVaR object tries to detect problem dimensions from the
inputs and, once set, subsequent inputs can undergo various scalar or matrix expansion
operations that simplify the overall process to formulate a problem. In addition, a
PortfolioCVaR object is a value object so that, given portfolio
p, the following code creates two objects, p
and q, that are
distinct:
q = PortfolioCVaR(p, ...)
After creating a PortfolioCVaR object, you can use the associated
object functions to set portfolio constraints, analyze the efficient frontier, and
validate the portfolio model.
For more detailed information on the theoretical basis for conditional value-at-risk portfolio optimization, see Portfolio Optimization Theory.
Creation
Description
p = PortfolioCVaRPortfolioCVaR object for conditional value-at-risk
portfolio optimization and analysis. You can then add elements to the
PortfolioCVaR object using the supported "add" and
"set" functions. For more information, see Creating the PortfolioCVaR Object.
p = PortfolioCVaR(Name,Value)PortfolioCVaR object (p) and
sets Properties using name-value
pairs. For example, p =
PortfolioCVaR('AssetList',Assets(1:12)). You can specify
multiple name-value pairs.
p = PortfolioCVaR(p,Name,Value)PortfolioCVaR object (p)
using a previously created PortfolioCVaR object
p and sets Properties using name-value
pairs. You can specify multiple name-value pairs.
Input Arguments
Output Arguments
Properties
Object Functions
setAssetList | Set up list of identifiers for assets |
setInitPort | Set up initial or current portfolio |
setDefaultConstraints | Set up portfolio constraints with nonnegative weights that sum to 1 |
estimateAssetMoments | Estimate mean and covariance of asset returns from data |
setCosts | Set up proportional transaction costs for portfolio |
addEquality | Add linear equality constraints for portfolio weights to existing constraints |
addGroupRatio | Add group ratio constraints for portfolio weights to existing group ratio constraints |
addGroups | Add group constraints for portfolio weights to existing group constraints |
addInequality | Add linear inequality constraints for portfolio weights to existing constraints |
getBounds | Obtain bounds for portfolio weights from portfolio object |
getBudget | Obtain budget constraint bounds from portfolio object |
getCosts | Obtain buy and sell transaction costs from portfolio object |
getEquality | Obtain equality constraint arrays from portfolio object |
getGroupRatio | Obtain group ratio constraint arrays from portfolio object |
getGroups | Obtain group constraint arrays from portfolio object |
getInequality | Obtain inequality constraint arrays from portfolio object |
getOneWayTurnover | Obtain one-way turnover constraints from portfolio object |
setGroups | Set up group constraints for portfolio weights |
setInequality | Set up linear inequality constraints for portfolio weights |
setBounds | Set up bounds for portfolio weights for portfolio |
setMinMaxNumAssets | Set cardinality constraints on the number of assets invested in a portfolio |
setBudget | Set up budget constraints for portfolio |
setConditionalBudget | Set up conditional budget constraints for portfolio |
setCosts | Set up proportional transaction costs for portfolio |
setDefaultConstraints | Set up portfolio constraints with nonnegative weights that sum to 1 |
setEquality | Set up linear equality constraints for portfolio weights |
setGroupRatio | Set up group ratio constraints for portfolio weights |
setInitPort | Set up initial or current portfolio |
setOneWayTurnover | Set up one-way portfolio turnover constraints |
setTurnover | Set up maximum portfolio turnover constraint |
checkFeasibility | Check feasibility of input portfolios against portfolio object |
estimateBounds | Estimate global lower and upper bounds for set of portfolios |
estimateFrontier | Estimate specified number of optimal portfolios on the efficient frontier |
estimateFrontierByReturn | Estimate optimal portfolios with targeted portfolio returns |
estimateFrontierByRisk | Estimate optimal portfolios with targeted portfolio risks |
estimateFrontierLimits | Estimate optimal portfolios at endpoints of efficient frontier |
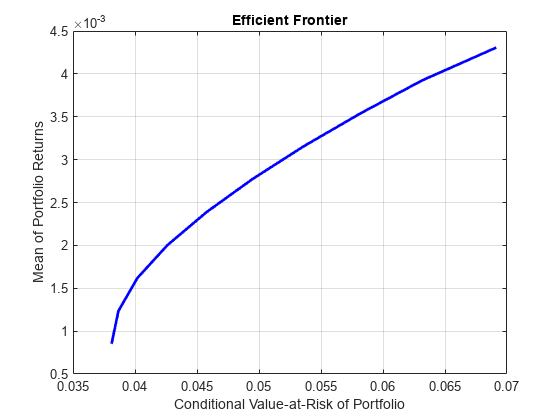
plotFrontier | Plot efficient frontier |
estimatePortReturn | Estimate mean of portfolio returns |
estimatePortRisk | Estimate portfolio risk according to risk proxy associated with corresponding object |
setSolver | Choose main solver and specify associated solver options for portfolio optimization |
setProbabilityLevel | Set probability level for VaR and CVaR calculations |
setScenarios | Set asset returns scenarios by direct matrix |
getScenarios | Obtain scenarios from portfolio object |
simulateNormalScenariosByData | Simulate multivariate normal asset return scenarios from data |
simulateNormalScenariosByMoments | Simulate multivariate normal asset return scenarios from mean and covariance of asset returns |
estimateScenarioMoments | Estimate mean and covariance of asset return scenarios |
estimatePortVaR | Estimate value-at-risk for PortfolioCVaR object |
estimatePortStd | Estimate standard deviation of portfolio returns |
Examples
More About
References
[1] For a complete list of references for the PortfolioCVaR object, see Portfolio Optimization.
Version History
Introduced in R2012bSee Also
plotFrontier | estimateFrontier | setScenarios | Portfolio | PortfolioMAD | nearcorr
Topics
- Creating the PortfolioCVaR Object
- Common Operations on the PortfolioCVaR Object
- Working with CVaR Portfolio Constraints Using Defaults
- Asset Returns and Scenarios Using PortfolioCVaR Object
- Estimate Efficient Portfolios for Entire Frontier for PortfolioCVaR Object
- Estimate Efficient Frontiers for PortfolioCVaR Object
- Postprocessing Results to Set Up Tradable Portfolios
- Hedging Using CVaR Portfolio Optimization
- Bond Portfolio CVaR Optimization Using Diebold-Li Model
- Portfolio Optimization Theory
- PortfolioCVaR Object Workflow
- PortfolioCVaR Object Properties and Functions
- Working with PortfolioCVaR Objects
- Setting and Getting Properties
- Displaying PortfolioCVaR Objects
- Saving and Loading PortfolioCVaR Objects
- Estimating Efficient Portfolios and Frontiers
- Arrays of PortfolioCVaR Objects
- Subclassing PortfolioCVaR Objects
- Conventions for Representation of Data
- Supported Constraints for Portfolio Optimization Using PortfolioCVaR Object
- Adding Constraints to Satisfy UCITS Directive
- Choosing and Controlling the Solver for PortfolioCVaR Optimizations
- Choose MINLP Solvers for Portfolio Problems