smoothPathSpline
Smooth vehicle path using cubic spline interpolation
Syntax
Description
[
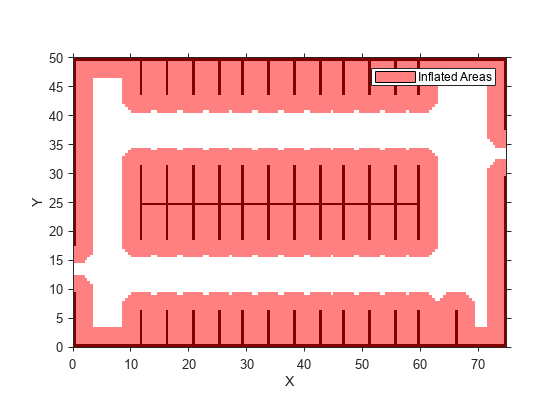
generates a smooth vehicle path, consisting of poses,directions] = smoothPathSpline(refPoses,refDirections,numSmoothPoses)numSmoothPoses
discretized poses, by fitting the input reference path poses to a cubic spline. Given the
input reference path directions, smoothPathSpline also returns the
directions that correspond to each pose.
Use this function to convert a C1-continuous vehicle path to
a C2-continuous path. C1-continuous
paths include the driving.DubinsPathSegment or driving.ReedsSheppPathSegment paths that you can plan using a pathPlannerRRT
object. For more details on these path types, see C1-Continuous and C2-Continuous Paths.
You can use the returned poses and directions with a vehicle controller, such as the
lateralControllerStanley function.
[
specifies a minimum separation threshold between poses. If the distance between two poses is
smaller than poses,directions] = smoothPathSpline(refPoses,refDirections,numSmoothPoses,minSeparation)minSeparation, the function uses only one of the poses for
interpolation.
[___,
also returns the cumulative path length and signed path curvature at each returned pose,
using any of the previous syntaxes. Use these values to generate a velocity profile along
the path. cumLengths,curvatures] = smoothPathSpline(___)
Examples
Input Arguments
Output Arguments
More About
Tips
To check if a smooth path is collision-free, specify the smooth poses as an input to the
checkPathValidityfunction.
Algorithms
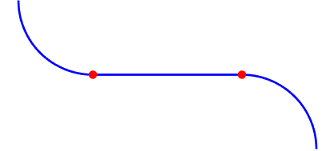
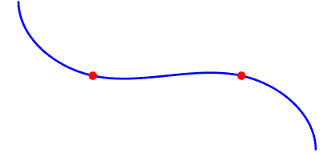
The path-smoothing algorithm interpolates a parametric cubic spline that passes through all input reference pose points. The parameter of the spline is the cumulative chord length at these points. [1]
The tangent direction of the smoothed output path approximately matches the orientation angle of the vehicle at the starting and goal poses.
References
[1] Floater, Michael S. "On the Deviation of a Parametric Cubic Spline Interpolant from Its Data Polygon." Computer Aided Geometric Design. Vol. 25, Number 3, 2008, pp. 148–156.
[2] Lepetic, Marko, Gregor Klancar, Igor Skrjanc, Drago Matko, and Bostjan Potocnik. "Time Optimal Path Planning Considering Acceleration Limits." Robotics and Autonomous Systems. Vol. 45, Numbers 3–4, 2003, pp. 199–210.
Extended Capabilities
Version History
Introduced in R2019a