Use Deep Learning to Approximate Barrier Option Prices with Heston Model
This example shows how to use Deep Learning Toolbox™ to train a network and obtain predictions on barrier option prices with a Heston model.
Barrier Option
The barrier option is an option where the payoff depends on whether the underlying asset crosses the predetermined trigger value (barrier level) during the life of the option. Barrier options are attractive because they are less expensive than the corresponding vanilla options. For more information, see Barrier Option (Financial Instruments Toolbox).
Heston Model
The Heston model is an extension of the Black-Scholes model, where the volatility (square root of variance) is no longer assumed to be constant, and the variance follows a stochastic (CIR) process. The Heston model allows modeling the implied volatility smiles observed in the market where options with identical expiration dates show increasing volatility as the options become more in-the-money (ITM) or out-of-the-money (OTM).
The stochastic differential equation is:
where
— Continuous risk-free rate
— Asset price at time
— Asset price variance at time
— Initial variance of the asset price at
— Long-term variance level
— Mean reversion speed for the variance
— Volatility of the variance
— Correlation between the Wiener processes and
Barrier option prices are usually computed using Monte Carlo simulation in the Heston setting since there is no closed-form solution available. However, a Monte Carlo simulation is computationally expensive, and when pricing instruments for financial markets, pricing speed is crucial. This example demonstrates using a vanilla neural network to speed up the barrier option pricing by learning the results from a Monte Carlo simulation. The neural network provides a highly efficient approximation technique. Although the off-line training is time consuming, the on-line pricing is fast.
Define Parameters
Focusing on a barrier-up, knock-out call option, start by deciding on the ranges for the pricing parameters. Consider a scaled spot price (moneyness) instead of two separate parameters (asset spot price) and (strike). The barrier level is also scaled by strike value.
% Option parameter ranges. % The first value defines the lower bound % and the second value is the upper bound. moneyness = [0.6 1.2]; % S0/K maturity = [0.05 2]; upBarrier = [0.6 1.3]; % Up barrier/K % Model parameter ranges rate = [0 0.05]; kappa = [0.3 2]; theta = [0.05 0.2]; sigma = [0.05 0.5]; v0 = [0.05 0.2]; rho = [-0.9 -0.1]; % Call option parameters optSpec = "call"; exerciseStyle = "european"; barriertype = "uo"; % Simulation parameter nTrials = 1000; % Set the random generator seed for reproducibility. % rng('default')
Gather Data
Sample the parameter combinations by using a quasi-Monte Carlo sampling method (sobolset (Statistics and Machine Learning Toolbox)) that is based on Sobol sequences which possess good uniformity properties. A Sobol sequence uses a base of 2 to form successively finer uniform partitions of the unit interval, and then reorders the coordinates in each dimension.
Quasi = sobolset(9,'Skip',1024); Quasi = scramble(Quasi,'MatousekAffineOwen'); inputs = Quasi(1:24e4, :); % Initial 240000 samples % Column number for each parameter in the inputs array. iMoneyness = 1;iTime = 2;iRate = 3;iCorr = 4;iKappa = 5;iTheta = 6;iSigma = 7;iV0 = 8;iBarrier = 9; inputs(:,iMoneyness) = inputs(:,iMoneyness)*(moneyness(2)-moneyness(1))+moneyness(1); % Moneyness S0/K inputs(:,iTime) = inputs(:,iTime)*(maturity(2)-maturity(1))+maturity(1); % Maturity time inputs(:,iRate) = inputs(:,iRate)*(rate(2)-rate(1))+rate(1); % rate inputs(:,iCorr) = inputs(:,iCorr)*(rho(2)-rho(1))+rho(1); % Correlation inputs(:,iKappa) = inputs(:,iKappa)*(kappa(2)-kappa(1))+kappa(1); % Mean reversion speed inputs(:,iTheta) = inputs(:,iTheta)*(theta(2)-theta(1))+theta(1); % Long-term variance inputs(:,iSigma) = inputs(:,iSigma)*(sigma(2)-sigma(1))+sigma(1); % Volatility of variance inputs(:,iV0) = inputs(:,iV0)*(v0(2)-v0(1))+v0(1); % Initial variance V0 inputs(:,iBarrier) = inputs(:,iBarrier)*(upBarrier(2)-upBarrier(1))+upBarrier(1); % UPbarrier/K
Remove the parameter combinations where the barrier levels are not greater than the initial spot prices.
% Barrier level should be higher than the initial spot price.
invalid = inputs(:,iBarrier)<=inputs(:,iMoneyness);
inputs(invalid,:) = [];Calculate Barrier Option Prices Using Monte Carlo Simulation
After you create the parameter space, calculate the prices of the Barrier (Financial Instruments Toolbox) option by Monte Carlo simulation using the object-based pricing framework in Financial Instrument Toolbox™. Specifically, use ratecurve (Financial Instruments Toolbox), Heston (Financial Instruments Toolbox), Barrier (Financial Instruments Toolbox), and AssetMonteCarlo (Financial Instruments Toolbox) to create the objects required to price the Barrier (Financial Instruments Toolbox) option. To avoid waiting for the Monte Carlo simulation, load the calculated prices for the example by setting the doMCPricing flag to false.
doMCPricing = false; if doMCPricing % Calculate the prices using the AssetMonteCarlo pricer. Settle = datetime(2021,2,1); Price = nan(size(inputs,1),1); for i = 1:size(inputs,1) AssetPrice = inputs(i,iMoneyness); Strike = 1; Barrier = inputs(i,iBarrier); V0 = inputs(i,iV0); ThetaV = inputs(i,iTheta); Kappa = inputs(i,iKappa); SigmaV = inputs(i,iSigma); RhoSV = inputs(i,iCorr); Rates = inputs(i,iRate); ExerciseDate = daysadd(Settle,round(inputs(i,iTime)*365),0); ZeroCurve = ratecurve('zero',Settle,ExerciseDate,Rates); hestonModel = finmodel("Heston",V0=V0,ThetaV=ThetaV,Kappa=Kappa,SigmaV=SigmaV,RhoSV=RhoSV); MCPricer = finpricer("AssetMonteCarlo",DiscountCurve=ZeroCurve,Model=hestonModel,SpotPrice=AssetPrice, ... SimulationDates=[Settle:days(2):ExerciseDate, ExerciseDate],numTrials=nTrials); CallBarrier = fininstrument("Barrier",ExerciseDate=ExerciseDate,Strike=Strike,OptionType=optSpec, ... Barriertype=barriertype,Barriervalue=Barrier,ExerciseStyle=exerciseStyle); Price(i) = price(MCPricer,CallBarrier); end else % Load the calculated prices for the example. load('DeepLearningBarrierHeston.mat','inputs','Price') end
If you do not use the calculated prices for the example by setting the doMCPricing flag to false, the following histogram shows the distribution of valuation times for each individual barrier option using a Monte Carlo method. This histogram demonstrates that it takes approximately 0.46 seconds to compute a single barrier option price. In this example, nTrials is set to 1e3 which is the number of trials in the Monte Carlo simulation to compute a single option price. The total time to compute prices for the sample size of 30,000 barrier options is approximately 3.9 hours, depending on the processor speed.

Define Neural Network
Different network architectures can help with the task of pricing barrier options using a Heston model. Choosing a neural network architecture requires balancing computation time against accuracy. This example uses multiple, fully-connected layers and Leaky ReLU activations.
numFeatures = size(inputs,2);
layers = [
featureInputLayer(numFeatures,Normalization='zscore')
fullyConnectedLayer(32,WeightsInitializer='he')
leakyReluLayer
fullyConnectedLayer(32,WeightsInitializer='he')
leakyReluLayer
fullyConnectedLayer(32,WeightsInitializer='he')
leakyReluLayer
fullyConnectedLayer(1,WeightsInitializer='he')
leakyReluLayer
];Visualize Network
You can visualize the network using the Deep Network Designer app or the analyzeNetwork function.
deepNetworkDesigner(layers)
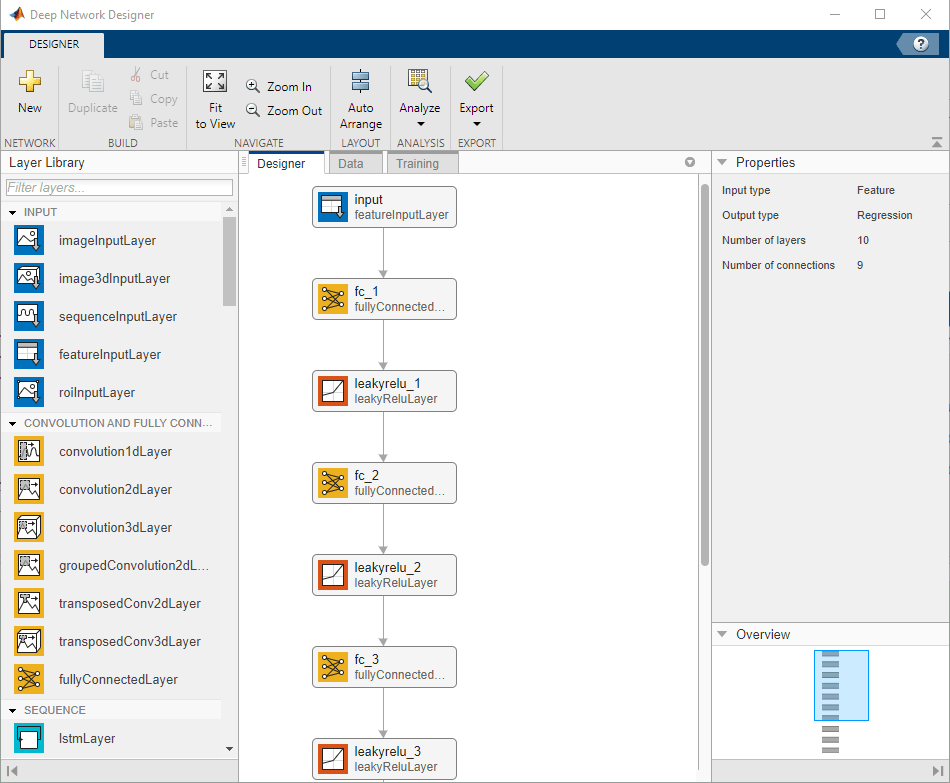
Train Network
Train the neural network by using the trainnet function. The function creates a hold-out set to test the trained network and allocates a validation set to monitor the overfitting during the training. By default, trainnet uses a GPU if one is available; otherwise, it uses a CPU. Training on a GPU requires Parallel Computing Toolbox™ and a supported GPU device. For information, see Deep Learning with MATLAB on Multiple GPUs.
n = size(Price,1); c = cvpartition(n,Holdout=1/5); % Hold out 1/5 of the data set for testing XTrain = inputs(training(c),:); % 4/5 of the input for training YTrain = Price(training(c),:); % 4/5 of the target for training XTest = inputs(test(c),:); % 1/5 of the input for testing YTest = Price(test(c),:); % 1/5 of the target for testing nTrain = size(XTrain,1); idx = randperm(nTrain,floor(nTrain*0.1)); % 10% validation data XValidation = XTrain(idx,:); XTrain(idx,:) = []; YValidation = YTrain(idx,:); YTrain(idx,:) = []; opts = trainingOptions('adam', ... MaxEpochs=30, ... Shuffle='every-epoch', ... Plots='none', ... Verbose=false, ... VerboseFrequency=50, ... MiniBatchSize=265, ... ValidationData={XValidation,YValidation}, ... ValidationFrequency=50, ... ValidationPatience=Inf, ... L2Regularization=1.9e-7, ... InitialLearnRate=8.8e-3, ... LearnRateSchedule='piecewise', ... LearnRateDropPeriod=4, ... LearnRateDropFactor=0.128, ... SquaredGradientDecayFactor=0.55, ... GradientDecayFactor=0.62); %opts.ExecutionEnvironment = "gpu"; % When using GPU doTraining = false; if doTraining % Train the network. net = trainnet(XTrain,YTrain,layers,"mean-squared-error",opts); else % Load the pretrained network for the example. load('DeepLearningBarrierHeston.mat','net') end
To avoid waiting for the training, load the pretrained network by setting the doTraining flag to false. To train the networks using trainnet, set the doTraining flag to true. The Training Progress window displays progress when Plots in trainingOptions is set as training-progress.
Test Network
After training the network model, you can use the predict function to evaluate the test data set containing 30,000 barrier options on this trained network. Compared to the histogram in Calculate Barrier Option Prices Using MonteCarlo Simulation where Monte Carlo simulation takes 0.46 seconds to price each barrier option (3.9 hours to price 30,000 barrier options), after the network model is trained, a data set containing 30,000 barrier option is evaluated in seconds.
% If testing on a GPU, then convert data to a gpuArray. if opts.ExecutionEnvironment == "gpu" && canUseGPU XTest = gpuArray(XTest); end YPred = predict(net,XTest);
To assess the performance of the network, calculate the mean-squared error (MSE) value.
mseTest = mean((YTest - YPred).^2)
mseTest = single
2.9402e-06
The following histogram shows the error distribution for the predicted barrier option price using Deep Learning Toolbox™ with respect to the calculated barrier option price using Financial Instrument Toolbox™.
figure histogram(YTest - YPred, Binwidth=1e-4) xlabel('Error Distribution') ylabel('Counts')

A plot of the calculated prices and predicted prices shows the performance of the network for the Heston model using the test data.
figure plot(YTest,YPred,'.',[min(YTest),max(YTest)],[min(YTest),max(YTest)],'r') xlabel('Scaled Actual Price') ylabel('Scaled Predicted Price') title('Predictions on Test Data')

References
[1] Goodfellow, I., Y. Bengio, and A. Courville. Deep Learning. MIT Press, 2016.
[2] Niederreiter, H. "Random Number Generation and Quasi-Monte Carlo Methods." Society for Industrial and Applied Mathematics, 1992.
See Also
Barrier (Financial Instruments Toolbox) | Heston (Financial Instruments Toolbox) | AssetMonteCarlo (Financial Instruments Toolbox) | Deep Network Designer | trainnet | trainingOptions | dlnetwork