fitoptions
Create or modify fit options object
Syntax
Description
fitOptions = fitoptionsfitOptions.
fitOptions = fitoptions(libraryModelName)
fitOptions = fitoptions(libraryModelName,Name,Value)Name,Value pair arguments.
fitOptions = fitoptions(fitType)fitType. Use this syntax to work with fit options for custom models.
fitOptions = fitoptions(Name,Value)Name,Value pair arguments.
newOptions = fitoptions(fitOptions,Name,Value)fitOptions and returns updated fit options in newOptions with new options specified by one or more Name,Value pair arguments.
newOptions = fitoptions(options1,options2)options1 and options2 in newOptions.
If
Methodagrees, the nonempty values for the properties inoptions2override the corresponding values inoptions1innewOptions.If
Methoddiffers,newOptionscontains theoptions1value forMethodand values fromoptions2forNormalize,Exclude, andWeights.
Examples
Create the default fit options object and set the option to center and scale the data before fitting.
options = fitoptions;
options.Normal = 'on'options =
basefitoptions with properties:
Normalize: 'on'
Exclude: []
Weights: []
Method: 'None'
options = fitoptions('gauss2')options =
nlsqoptions with properties:
StartPoint: []
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
Lower: [-Inf -Inf 0 -Inf -Inf 0]
Upper: []
ConstraintPoints: []
TolCon: 1.0000e-06
Robust: 'Off'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
Create fit options for a cubic polynomial and set center and scale and robust fitting options.
options = fitoptions('poly3', 'Normalize', 'on', 'Robust', 'Bisquare')
options =
llsqoptions with properties:
Lower: []
Upper: []
ConstraintPoints: []
TolCon: 1.0000e-06
Robust: 'Bisquare'
Normalize: 'on'
Exclude: []
Weights: []
Method: 'LinearLeastSquares'
options = fitoptions('Method', 'LinearLeastSquares')
options =
llsqoptions with properties:
Lower: []
Upper: []
ConstraintPoints: []
TolCon: 1.0000e-06
Robust: 'Off'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'LinearLeastSquares'
Create a fitoptions object for a linear interpolant fit with nearest neighbor extrapolation.
linearoptions = fitoptions("linearinterp",ExtrapolationMethod="nearest")
linearoptions =
linearinterpoptions with properties:
ExtrapolationMethod: 'nearest'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'LinearInterpolant'
Create a second fitoptions object for a cubic interpolant fit with nearest neighbor extrapolation.
cubicoptions = fitoptions("cubicinterp",ExtrapolationMethod="nearest")
cubicoptions =
cubicsplineinterpoptions with properties:
ExtrapolationMethod: 'nearest'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'CubicSplineInterpolant'
You can use the fit options in linearoptions to create a linearinterp fit object using the fit function. Use cubicoptions to create a cubicinterp fit.
Modifying the default fit options object is useful when you want to set the Normalize, Exclude, or Weights properties, and then fit your data using the same options with different fitting methods. For example, the following uses the same fit options to fit different library model types.
load census options = fitoptions; options.Normalize = 'on'; f1 = fit(cdate,pop,'poly3',options); f2 = fit(cdate,pop,'exp1',options); f3 = fit(cdate,pop,'cubicspline',options)
f3 =
Cubic interpolating spline:
f3(x) = piecewise polynomial computed from p
with cubic extrapolation
where x is normalized by mean 1890 and std 62.05
Coefficients:
p = coefficient structure
Find the smoothing parameter. Data-dependent fit options such as the smooth parameter are returned in the third output argument of the fit function.
load census [f,gof,out] = fit(cdate,pop,'SmoothingSpline'); smoothparam = out.p
smoothparam = 0.0089
Modify the default smoothing parameter for a new fit.
options = fitoptions('Method','SmoothingSpline',... 'SmoothingParam',0.0098); [f,gof,out] = fit(cdate,pop,'SmoothingSpline',options);
Create a Gaussian fit, inspect the confidence intervals, and specify lower bound fit options to help the algorithm.
Create a noisy sum of two Gaussian peaks, one with a small width, and one with a large width.
a1 = 1; b1 = -1; c1 = 0.05; a2 = 1; b2 = 1; c2 = 50; x = (-10:0.02:10)'; gdata = a1*exp(-((x-b1)/c1).^2) + ... a2*exp(-((x-b2)/c2).^2) + ... 0.1*(rand(size(x))-.5); plot(x,gdata)

Fit the data using the two-term Gaussian library model.
gfit = fit(x,gdata,'gauss2') gfit =
General model Gauss2:
gfit(x) = a1*exp(-((x-b1)/c1)^2) + a2*exp(-((x-b2)/c2)^2)
Coefficients (with 95% confidence bounds):
a1 = -0.1451 (-1.485, 1.195)
b1 = 9.725 (-14.7, 34.15)
c1 = 7.117 (-15.84, 30.07)
a2 = 14.08 (-1.962e+04, 1.965e+04)
b2 = 607.4 (-3.197e+05, 3.209e+05)
c2 = 376 (-9.745e+04, 9.82e+04)
plot(gfit,x,gdata)
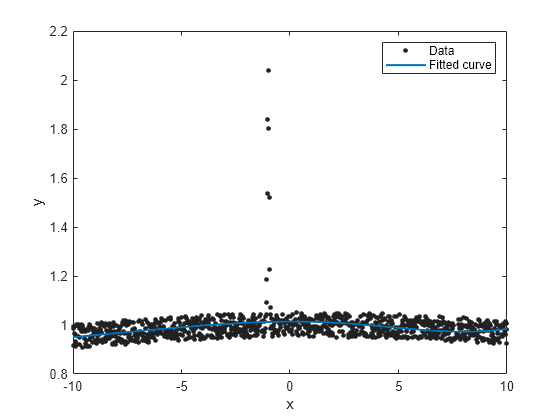
The algorithm is having difficulty, as indicated by the wide confidence intervals for several coefficients.
To help the algorithm, specify lower bounds for the nonnegative amplitudes a1 and a2 and widths c1, c2.
options = fitoptions('gauss2', 'Lower', [0 -Inf 0 0 -Inf 0]);
Alternatively, you can set properties of the fit options using the form options.Property = NewPropertyValue.
options = fitoptions('gauss2');
options.Lower = [0 -Inf 0 0 -Inf 0];Recompute the fit using the bound constraints on the coefficients.
gfit = fit(x,gdata,'gauss2',options) gfit =
General model Gauss2:
gfit(x) = a1*exp(-((x-b1)/c1)^2) + a2*exp(-((x-b2)/c2)^2)
Coefficients (with 95% confidence bounds):
a1 = 1.005 (0.966, 1.044)
b1 = -1 (-1.002, -0.9988)
c1 = 0.0491 (0.0469, 0.0513)
a2 = 0.9985 (0.9958, 1.001)
b2 = 0.8059 (0.3879, 1.224)
c2 = 50.6 (46.68, 54.52)
plot(gfit,x,gdata)

This is a much better fit. You can further improve the fit by assigning reasonable values to other properties in the fit options object.
Create fit options and set lower bounds.
options = fitoptions('gauss2', 'Lower', [0 -Inf 0 0 -Inf 0])
options =
nlsqoptions with properties:
StartPoint: []
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
Lower: [0 -Inf 0 0 -Inf 0]
Upper: []
ConstraintPoints: []
TolCon: 1.0000e-06
Robust: 'Off'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
Make a new copy of the fit options and modify the robust parameter.
newoptions = fitoptions(options, 'Robust','Bisquare')
newoptions =
nlsqoptions with properties:
StartPoint: []
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
Lower: [0 -Inf 0 0 -Inf 0]
Upper: []
ConstraintPoints: []
TolCon: 1.0000e-06
Robust: 'Bisquare'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
Combine fit options.
options2 = fitoptions(options, newoptions)
options2 =
nlsqoptions with properties:
StartPoint: []
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
Lower: [0 -Inf 0 0 -Inf 0]
Upper: []
ConstraintPoints: []
TolCon: 1.0000e-06
Robust: 'Bisquare'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
Create a linear model fit type.
lft = fittype({'x','sin(x)','1'})lft =
Linear model:
lft(a,b,c,x) = a*x + b*sin(x) + c
Get the fit options for the fit type lft.
fo = fitoptions(lft)
fo =
llsqoptions with properties:
Lower: []
Upper: []
ConstraintPoints: []
TolCon: 1.0000e-06
Robust: 'Off'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'LinearLeastSquares'
Set the normalize fit option.
fo.Normalize = 'on'fo =
llsqoptions with properties:
Lower: []
Upper: []
ConstraintPoints: []
TolCon: 1.0000e-06
Robust: 'Off'
Normalize: 'on'
Exclude: []
Weights: []
Method: 'LinearLeastSquares'
Input Arguments
Library model to fit, specified as a character vector or string scalar. This table shows some common examples.
Library Model Name | Description |
|---|---|
| Linear polynomial curve |
| Linear polynomial surface |
| Quadratic polynomial curve |
| Piecewise linear interpolation |
| Piecewise cubic interpolation |
| Smoothing spline (curve) |
| Local linear regression (surface) |
'log10' | Base-10 logarithmic curve |
'logistic4' | Four-parameter logistic curve |
For a list of library model names, see Model Names and Equations.
Example: 'poly2'
Data Types: char | string
Model type to fit, specified as a fittype constructed with the fittype function. Use this to work with fit options for custom models.
Algorithm options, specified as a fitoptions object created using the fitoptions function.
Algorithm options to combine, constructed using the fitoptions function.
Algorithm options to combine, constructed using the fitoptions function.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Method','NonlinearLeastSquares','Lower',[0,0],'Upper',[Inf,max(x)],'Startpoint',[1 1] specifies fitting method, bounds, and start points.
Options for All Fitting Methods
Option to center and scale the data, specified as the comma-separated pair consisting of 'Normalize' and 'on' or 'off'.
Data Types: char
Points to exclude from the fit, specified as the comma-separated pair consisting of 'Exclude' and one of:
An expression describing a logical vector, e.g.,
x > 10.A vector of integers indexing the points you want to exclude, e.g.,
[1 10 25].A logical vector for all data points where
truerepresents an outlier, created byexcludedata.
For examples, see fit.
Weights for the fit, specified as the comma-separated pair consisting of 'Weights' and a vector the same size as number of data points.
Data Types: double
Fitting method, specified as the comma-separated pair consisting of 'Method' and one of the fitting methods in this table.
Fitting Method | Description |
|---|---|
| Nearest neighbor interpolation |
| Linear interpolation |
| Piecewise cubic Hermite interpolation (curves only) |
| Cubic spline interpolation |
| Biharmonic surface interpolation |
| Smoothing spline |
| Lowess smoothing (surfaces only) |
| Linear least squares |
| Nonlinear least squares |
Data Types: char | string
Interpolation Options
Extrapolation method for an interpolant fit, specified as one of the following values:
| Value | Description | Supported Fits |
|---|---|---|
"auto" | Default value for all interpolant fit types. Set | All interpolant fit types and |
"none" | No extrapolation. When you use | Curve fits — Surface
fits —
Curve
and surface fits — |
"linear" | Linear extrapolation based on boundary gradients | Surface fits — Curve
and surface fits —
|
"nearest" | Nearest neighbor extrapolation. This method evaluates to the value of the nearest point on the boundary of the fitting data's convex hull. | Curve fits — Surface
fits —
Curve
and surface fits —
|
"thinplate" | Thin-plate spline extrapolation. This method extends the thin-plate interpolating spline outside of the fitting data's convex hull. For more information, see | Surface fits — |
"biharmonic" | Biharmonic spline extrapolation. This method extends the biharmonic interpolating spline outside of the fitting data's convex hull. | Surface fits — |
"pchip" | Piecewise cubic hermite interpolating polynomial (PCHIP) extrapolation. This method extends a shape-preserving PCHIP outside of the fitting data's convex hull. For more information, see | Curve fits — |
"cubic" | Cubic spline extrapolation. This method extends a cubic interpolating spline outside of the fitting data's convex hull. | Curve fits — |
Data Types: char | string
Smoothing Options
Smoothing parameter, specified as the comma-separated pair consisting of 'SmoothingParam' and a scalar value between 0 and 1. The default value depends on the data set. Only available if the Method is SmoothingSpline. For more information, see About Smoothing Splines.
Data Types: double
Proportion of data points to use in local regressions, specified as the comma-separated pair consisting of 'Span' and a scalar value between 0 and 1. Only available if the Method is LowessFit.
Data Types: double
Linear and Nonlinear Least-Squares Options
Robust linear least-squares fitting method, specified as the comma-separated pair consisting of 'Robust' and one of these values:
'LAR'specifies the least absolute residual method.'Bisquare'specifies the bisquare weights method.
Available when the Method is LinearLeastSquares or NonlinearLeastSquares.
Data Types: char
Lower bounds on the coefficients to be fitted, specified as the comma-separated pair consisting of 'Lower' and a vector. The default value is an empty vector, indicating that the fit is unconstrained by lower bounds. If bounds are specified, the vector length must equal the number of coefficients. Find the order of the entries for coefficients in the vector value by using the coeffnames function. For an example, see fit. Individual unconstrained lower bounds can be specified by -Inf.
Available when the Method is LinearLeastSquares or NonlinearLeastSquares.
Data Types: double
Upper bounds on the coefficients to be fitted, specified as the comma-separated pair consisting of 'Upper' and a vector. The default value is an empty vector, indicating that the fit is unconstrained by upper bounds. If bounds are specified, the vector length must equal the number of coefficients. Find the order of the entries for coefficients in the vector value by using the coeffnames function. For an example, see fit. Individual unconstrained upper bounds can be specified by +Inf.
Available when the Method is LinearLeastSquares or NonlinearLeastSquares.
Data Types: logical
Since R2025a
Points to fit through, specified as a n-by-2 numeric
matrix for curves and n-by-3 numeric matrix for
surfaces. Each row represents one constraint point and each column represents the
x,y or z coordinate for the
point. The number of constraint points cannot be greater than the number of coefficients
in the specified fitType. You can find the number of coefficients
in the fittype using numcoeffs. Specifying the maximum
number of constraint points results in only one solution, with the resulting solution
independent of the input data.
Note
You must have Optimization Toolbox™ installed to use constraint points for fitting a model.
Available when the Method is LinearLeastSquares
or NonlinearLeastSquares.
Example: [0 0; 1 5]
Data Types: double
Since R2025a
Tolerance for constraint points, specified as a nonnegative numeric scalar. This is the upper bound of the absolute numerical difference between the provided constraint point and the actual point the fit passes through, before a constraint violation occurs.
If ConstraintPoints name-value argument is not specified,
TolCon has no effect.
Note
TolCon operates differently from other tolerances. If
TolCon is satisfied, the solver still continues, unless it
is halted for another reason. A solver does not halt simply because
TolCon is satisfied.
Available when the Method is LinearLeastSquares
or NonlinearLeastSquares.
Data Types: double
Nonlinear Least-Squares Options
Initial values for the coefficients, specified as the comma-separated pair consisting of 'StartPoint' and a vector. Find the order of the entries for coefficients in the vector value by using the coeffnames function. For an example, see fit.
If no start points (the default value of an empty vector) are passed to the fit function, starting points for some library models are determined heuristically. For rational and Weibull models, and all custom nonlinear models, the toolbox selects default initial values for coefficients uniformly at random from the interval (0,1). As a result, multiple fits using the same data and model might lead to different fitted coefficients. To avoid this, specify initial values for coefficients with a vector value for the StartPoint property.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Algorithm to use for the
fitting procedure, specified as "Levenberg-Marquardt",
"Trust-Region" or "Interior-Point". The
algorithm must be "Interior-Point" when
ConstraintPoints are provided. If another algorithm is
specified, the software will switch the algorithm to
"Interior-Point". The Optimization Toolbox is required to use the Interior-Point algorithm.
Available when the Method is
NonlinearLeastSquares.
Data Types: char
Maximum change in coefficients for finite difference gradients, specified as the comma-separated pair consisting of 'DiffMaxChange' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Minimum change in coefficients for finite difference gradients, specified as the comma-separated pair consisting of 'DiffMinChange' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Display option in the command window, specified as the comma-separated pair consisting of 'Display' and one of these options:
'notify'displays output only if the fit does not converge.'final'displays only the final output.'iter'displays output at each iteration.'off'displays no output.
Available when the Method is NonlinearLeastSquares.
Data Types: char
Maximum number of evaluations of the model allowed, specified as the comma-separated pair consisting of 'MaxFunEvals' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Maximum number of iterations allowed for the fit, specified as the comma-separated pair consisting of 'MaxIter' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Termination tolerance on the model value, specified as the comma-separated pair consisting of 'TolFun' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Termination tolerance on the coefficient values, specified as the comma-separated pair consisting of 'TolX' and a scalar.
Available when the Method is NonlinearLeastSquares.
Data Types: double
Output Arguments
Algorithm options, returned as an options object.
New algorithm options, returned as an options object.
Version History
Introduced before R2006aFor regression fittypes, you can specify fixed points to fit the curve or surface through
by using the new ConstraintPoints name-value argument. You can also
provide the constraint tolerance using the new TolCon name-value
argument. The software fits the curve of surface through the constraint point using the new
"Interior-Point" algorithm.
Note
You must have Optimization Toolbox installed to use constraint points for fitting a model.
Starting in R2024a, you can create natural neighbor interpolant surface fits. For more information, see List of Library Models for Curve and Surface Fitting.
Starting in 2023b, you can specify additional extrapolation methods for interpolant curve fits by using the ExtrapolationMethod name-value argument. For more information, see Extrapolation for Interpolant Fit Types.
Starting in R2023b, you can specify sigmoidal and logarithmic fit types for curve fits. For more information, see List of Library Models for Curve and Surface Fitting.
Starting in R2023a, fitoptions returns value objects instead of handle objects. For more information, see Comparison of Handle and Value Classes.
Starting in 2023a, you can specify the extrapolation method for interpolant fits by using the ExtrapolationMethod name-value argument. For curve fits, Curve Fitting Toolbox™ supports only the default extrapolation methods available in previous releases.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)