OFDM Autoencoder for Wireless Communications
This example shows how to model an end-to-end orthogonal frequency division modulation (OFDM) communications system with an autoencoder to reliably transmit information bits over a wireless channel.
Introduction
This example uses an autoencoder together with OFDM modulator, demodulator, channel estimator and equalizer layers to design and implement a multi-carrier communications system.
In this example, you will learn how to:
Create OFDM modulation and demodulation layers using the
ofdmmodandofdmdemodfunctions.Create an OFDM equalization layer using the
ofdmChannelResponsefunction.Train a convolutional neural network with embedded OFDM modulation, demodulation and equalization over a Rayleigh fading channel.
Extract the learned encoder and decoder from the trained neural network.
Run BLER simulations to compare error rate performance of a conventional OFDM link to an AI-based OFDM link.
For an equivalent single-carrier communications system, see the Autoencoders for Wireless Communications example.
OFDM-based Autoencoder System
This block diagram shows a wireless autoencoder communications system. The encoder (transmitter) first maps each set of information bits in a sequence into a message such that , where , to form messages. Each of the messages, , is mapped to real-valued channel uses, , which results in an effective coding rate of data bits per real channel use. Then, every two real channel uses are mapped into a complex symbol to create . The normalization layer of the encoder imposes constraints on to further restrict the encoded symbols. The layer can be used to enforce one of the following constraints:
Energy constraint:
Average power constraint:
Normalized symbols are mapped onto the OFDM subcarriers and passed through a multipath fading channel with additive white Gaussian noise.
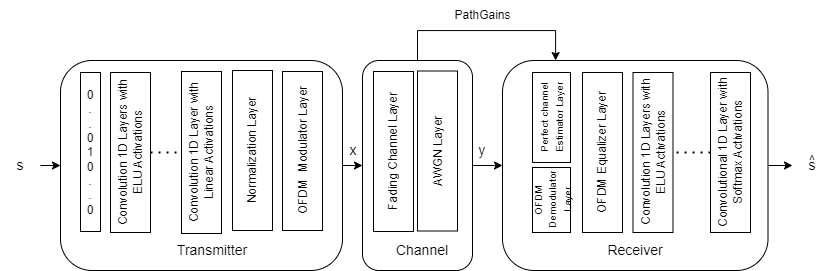
The transmitter encodes and outputs encoded symbols, . The channel impairs the encoded symbols to generate . The receiver decodes and outputs estimate, , of the transmitted message .
The input message is a one-hot vector , whose elements are all zeros except the one. is filtered through a MISO multipath fading channel with AWGN with a given signal to noise power ratio, .
Generate and Preprocess Data
The input to the transmitter is a random sequence of bits. bits can create distinct messages or input symbols. The input symbol is a categorical feature from the set of . As the number of possible input symbols increases, the number of training sequences must increase to give the network a chance to experience many input combinations. The same is true for the number of validation sequences. Set number of input bits per symbol to 4.
k =4; % Information bits per symbol M = 2^k; % Size of information symbols set numTrainSeq = 1e3 * M; numValidationSeq = 1e2 * M;
The autoencoder neural network best works with one-hot inputs and classifies each input symbol as one of the categorical values, . Convert random input symbols into a one-hot array using the onehotencode (Deep Learning Toolbox) function. Place the one-hot value to the first dimension (rows) and input symbols to the second dimension (columns).
dTrain = randi([0 M-1],1,5)
dTrain = 1×5
13 14 2 14 10
trainSymbolsTemp = onehotencode(dTrain,1,"ClassNames",0:M-1)trainSymbolsTemp = 16×5
0 0 0 0 0
0 0 0 0 0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 1
0 0 0 0 0
0 0 0 0 0
1 0 0 0 0
0 1 0 1 0
⋮
trainLabelsTemp = categorical(dTrain)
trainLabelsTemp = 1×5 categorical
13 14 2 14 10
The autoencoder uses a sequenceInputLayer (Deep Learning Toolbox). Each sequence represents one or more OFDM symbols. Set the number of subcarriers, , to 128 and the number of OFDM symbols per training sequence to 1.
Nfft =128; % Number of OFDM data subcarriers Nsym = Nfft; % Number of modulated symbols per training sequence
Generate the training data set as a cell array of numTrainSeq sequences. Each sequence has the one hot encoding on the first dimension (rows) and the symbols on the second dimension (columns).
dTrain = randi([0 M-1],numTrainSeq,1,Nsym); trainSeq = onehotencode(dTrain,2,"ClassNames",0:M-1); trainSeq = mat2cell(trainSeq,ones(1,numTrainSeq)); trainSeq = cellfun(@squeeze,trainSeq,"UniformOutput",false);
Similarly, generate the validation data.
dValid = randi([0 M-1],numValidationSeq,1,Nsym); validationSeq = onehotencode(dValid,2,"ClassNames",0:M-1); validationSeq = mat2cell(validationSeq,ones(1,numValidationSeq)); validationSeq = cellfun(@squeeze,validationSeq,'UniformOutput',false);
The size of training symbols is . The size of training labels is .
numTrainSeq = length(trainSeq)
numTrainSeq = 16000
sizeTrainSymbols = size(trainSeq{1})sizeTrainSymbols = 1×2
16 128
Define and Train Neural Network Model
The second step of designing an AI-based system is to define and train the neural network model.
Define Neural Network
This example uses a modified version of the autoencoder neural network proposed in [2]. Three 1D convolutional layers map bits (in the form of length one-hot arrays) into real numbers, resulting in a rate communications system. After normalization, the OFDM modulator layer maps these real numbers into complex valued symbols and assigns each symbol to a subcarrier. To ensure that the OFDM modulator layer receives at least a full OFDM symbol at a time, set minimum input length, MinLength, of the sequence input layer to . Therefore, the input to the neural network is a sequence of one-hot values with size . This network uses the sequenceInputLayer function with number of features and sequence length of at least .
The reliability of the communication link can be increased through multiple uses of the channel for the same information symbol, which is also known as coding gain. An autoencoder can learn to leverage this increased number of channel uses, . The following trains an OFDM-based (8,4) autoencoder, which is equivalent to having a coding rate, , of 1/2. Set to 8.
The fading channel layer transmits the modulated symbols over a fading channel using ntx transmit antennas and adds AWGN. The impaired symbols are received by an OFDM demodulation layer using one receive antenna.
Train the neural network at several SNR levels to ensure that the autoencoder can handle a range of SNR values without retraining. Set the minimum and maximum training SNR values to 0 dB and 12 dB, respectively.
minTrainSNR =0; % Min training SNR (dB) maxTrainSNR =
12; % Max training SNR (dB) n =
8; % (n/2) is the number of complex channel uses CPLength =
12; % Samples normalization =
"Average power"; % Normalization "Energy" | "Average power" ntx =
2; % Number of transmit antennas SCS = 240*1e3; % Subcarrier spacing in Hz Fs = SCS*Nfft/0.85; % Sampling frequency nSamples = (Nfft+CPLength)*n/2; inputLayer = sequenceInputLayer(M,Name="One-hot input",MinLength=Nfft);
Create an encoder using four 1D convolutional layers followed by layer normalization layers and elu activations.
encoderLayers = [convolution1dLayer(1,4,"Name","conv_1") layerNormalizationLayer eluLayer("Name","elu_1") convolution1dLayer(2,4,"Name","conv_2","Padding","causal") layerNormalizationLayer eluLayer("Name","elu_2") convolution1dLayer(2,4,"Name","conv_3","Padding","causal") layerNormalizationLayer eluLayer("Name","elu_3") convolution1dLayer(1,n,"Name","conv_4") helperAEWOFDMNormalizationLayer(Method=normalization)];
Similarly, create a decoder using five 1D convolutional layers followed by layer normalization layers and elu activations.
decoderLayers = [convolution1dLayer(1,128,"Name","conv_5") layerNormalizationLayer eluLayer("Name","elu_4") convolution1dLayer(3,128,"Name","conv_6","Padding","causal") layerNormalizationLayer eluLayer("Name","elu_5") convolution1dLayer(3,128,"Name","conv_7","Padding","causal") layerNormalizationLayer eluLayer("Name","elu_6") convolution1dLayer(3,128,"Name","conv_8","Padding","causal") layerNormalizationLayer eluLayer("Name","elu_7") convolution1dLayer(1,M,"Name","conv_9") softmaxLayer(Name="softmax")];
Add the input layer, an OFDM modulation layer, fading channel layer, OFDM demodulation and channel equalization custom layers to the encoder and decoder to create the OFDM Autoencoder. The helperAEWOFDMChannelLayer filters its input signal using multiple delay profiles and doppler frequency shifts. The layer then adds AWGN to the received signal.
ofdmAENet = dlnetwork([inputLayer encoderLayers helperAEWOFDMModLayer(Nfft,CPLength,Name="ofdmMod") helperAEWOFDMChannelLayer(ntx,Fs,minTrainSNR,maxTrainSNR,Name="fadingChannel") helperAEWOFDMDemodLayer(Nfft,CPLength,Name="ofdmDemod")]); ofdmEqualizeLayer = helperAEWOFDMEqualizeLayer(Nfft,ntx,Name="ofdmEqualize"); ofdmAENet = addLayers(ofdmAENet,ofdmEqualizeLayer); ofdmAENet = connectLayers(ofdmAENet,"ofdmDemod/out","ofdmEqualize/in1"); ofdmAENet = addLayers(ofdmAENet,decoderLayers); ofdmAENet = connectLayers(ofdmAENet,"ofdmEqualize/out","conv_5/in");
Use helperAEWOFDMChanResponseLayer to create an OFDM channel response layer that receives the time domain fading path gains, channel filter taps and channel filter delays and returns the equivalent channel response in the frequency domain to the equalization layer.
chanResponse = helperAEWOFDMChanResponseLayer(Nfft,CPLength,ntx,Name="channelResponse"); ofdmAENet = addLayers(ofdmAENet,chanResponse); ofdmAENet = connectLayers(ofdmAENet,"fadingChannel/out2","channelResponse/in1"); ofdmAENet = connectLayers(ofdmAENet,"fadingChannel/out3","channelResponse/in2"); ofdmAENet = connectLayers(ofdmAENet,"fadingChannel/out4","channelResponse/in3"); ofdmAENet = connectLayers(ofdmAENet,"channelResponse","ofdmEqualize/in2"); plot(ofdmAENet)

Use the analyzeNetwork (Deep Learning Toolbox) function to view the output size of each layer in the autoencoder.
analyzeNetwork(ofdmAENet)
Train Neural Network
To run this example quickly, load the pretrained network, trainedNet, saved in the MAT file OFDMAutoencoderNet.mat. To train the network from scratch, set trainNow flag to true. Set the training options using the trainingOptions (Deep Learning Toolbox) object and train the network using the trainnet (Deep Learning Toolbox) function. Training takes about 15 minutes on an Nvidia® GeForce RTX 3080 GPU with 12 GB.
trainNow =false; batchSize = 1000; fileName = sprintf("OFDMAENetK%d_Nfft%d_%d_Nt%d", ... k,Nfft,CPLength,ntx); if trainNow % Set training options options = trainingOptions("adam", ... InitialLearnRate=8e-3, ... MiniBatchSize=batchSize, ... MaxEpochs=100, ... OutputNetwork="best-validation-loss", ... Shuffle="every-epoch", ... ValidationData={validationSeq,validationSeq}, ... LearnRateSchedule="piecewise", ... LearnRateDropPeriod=20, ... LearnRateDropFactor=0.8, ... ValidationFrequency=ceil(numTrainSeq/batchSize), ... ValidationPatience=20, ... Verbose=true, ... VerboseFrequency=ceil(numTrainSeq/batchSize), ... InputDataFormats="CTB", ... TargetDataFormats="CTB"); %#ok<UNRCH> % Train the autoencoder network [trainedNet,trainInfo] = trainnet(trainSeq,trainSeq,ofdmAENet,"crossentropy",options); save(fileName+'_'+string(datetime('now', Format='dd_MM_HH_mm')) ,'trainedNet','trainInfo') else try load(fileName,"trainedNet") catch me if strcmp(me.identifier,'MATLAB:load:couldNotReadFile') error("Selected combination of parameters k, Nfft, CPLength, and ntx does not have a pretrained " + ... "network. Set trainNow to true.") else rethrow(me) end end end
Separate the network into encoder and decoder parts. The encoder starts with the input layer and ends after the wireless normalization layer.
for idxNormLayer = 1:length(trainedNet.Layers) if isa(trainedNet.Layers(idxNormLayer), "helperAEWOFDMNormalizationLayer") break end end lgraph = layerGraph(trainedNet.Layers(1:idxNormLayer)); txNet = dlnetwork(lgraph);
The decoder starts after the OFDM equalization layer and ends with the classification layer. Add a sequence input layer at the beginning.
for idxOFDMDemod = idxNormLayer+1:length(trainedNet.Layers) if isa(trainedNet.Layers(idxOFDMDemod),"nnet.cnn.layer.Convolution1DLayer") break end end lgraph = layerGraph( ... [sequenceInputLayer(n,MinLength=Nfft) trainedNet.Layers(idxOFDMDemod:end-1)]); rxNet = dlnetwork(lgraph);
Use the plot object function of the trained network objects to show the layer graphs of the full autoencoder, the extracted encoder network, and the extracted decoder network.
figure tiledlayout(2,2) nexttile([2 1]) plot(trainedNet) title("Autoencoder") nexttile plot(txNet) title("Encoder") nexttile plot(rxNet) title("Decoder")

Compare BLER of Autoencoder-based Link to a Conventional OFDM Link
Set up simulation parameters. The following parameters ensure the simulation runs in about one minute while providing acceptable BLER results. Increase the SNR range and maximum number of frames to get more reliable results for a wider range.
rng("default")
snrVec = 0:2:12;
symbolsPerFrame = Nfft;
minNumErrors = 100;
maxNumFrames = 1000;
M = 2^k;
traceBack = 32;
codeRate = 1/2;
ntx = 4;
dopplerShift = 5;Generate random integers in the [0 -1] range that represents random information bits. Encode these information bits into complex symbols with helperAEWOFDMEncode function. The helperAEWOFDMEncode function runs the encoder part of the autoencoder then maps the real valued vector into a complex valued vector such that the odd and even elements are mapped into the in-phase and the quadrature component of a complex symbol, respectively, where . In other words, treat the array as an interleaved complex array.
Pass the complex symbols through an AWGN channel. Decode the channel impaired complex symbols with the helperAEWOFDMDecode function.
BLER = zeros(length(snrVec),2); errorstats = zeros(length(snrVec),3); delayProfile = channelDelayProfile('A'); channel1 = comm.MIMOChannel(... NumTransmitAntennas=ntx, ... NumReceiveAntennas=1, ... SpatialCorrelationSpecification="None", ... PathDelays=delayProfile(1,:).*(100/1e9), ... AveragePathGains=delayProfile(2,:), ... MaximumDopplerShift=dopplerShift, ... SampleRate=Fs,... PathGainsOutputPort=true); channel2 = comm.MIMOChannel(... NumTransmitAntennas=ntx, ... NumReceiveAntennas=1, ... SpatialCorrelationSpecification="None", ... PathDelays=delayProfile(1,:).*(100/1e9), ... AveragePathGains=delayProfile(2,:), ... MaximumDopplerShift=dopplerShift, ... SampleRate=Fs,... PathGainsOutputPort=true); trellis = poly2trellis(7,[171 133]); errorRate = comm.ErrorRate(ReceiveDelay=traceBack);
The following code runs the simulation for each point for at least 100 block errors or at most 1000 frames. If Parallel Computing Toolbox™ is installed and a license is available, uncomment the parfor line to run the simulations on a parallel pool.
% parfor snrIdx = 1:length(snrVec) for snrIdx = 1:length(snrVec) snr = snrVec(snrIdx); disp("Simulating for SNR = " + snrVec(snrIdx)) numBlockErrors = 0; numConvBlockErrors = 0; frameCnt = 0; reset(errorRate) while (numBlockErrors < minNumErrors) ... && (frameCnt < maxNumFrames) %% Simulate OFDM link with AE % Generate random information symbols d = randi([0 M-1],symbolsPerFrame,1); % Run AE encoder x = helperAEWOFDMEncode(d,txNet); xOfdmMod = sqrt(Nfft)*ofdmmod(x,Nfft,CPLength); % Repeat transmitted signal over all tx antennas channelInput = sqrt(ntx)*repmat(xOfdmMod, [1 ntx]); % Filter through fading channel [channelOut, pathgains] = channel1(channelInput); % channelOut is Ns x Nr, pathgains is Ns x Np x Nt x Nr channelInfo = info(channel1); filtTaps = channelInfo.ChannelFilterCoefficients; filtDelays = channelInfo.ChannelFilterDelay; % Add AWGN noise sigPower = sum(abs(channelInput(:)).^2)/numel(channelInput); sigPowerdB = 10*log10(sigPower); y = awgn(channelOut,snr,sigPowerdB); % Perfect channel estimator hfreq = ofdmChannelResponse(pathgains,filtTaps,Nfft,CPLength, ... 1:Nfft,filtDelays); % hfreq is Nsc x Nsym x Nt x Nr hfreq = reshape(hfreq, Nfft,[], ntx, 1); % OFDM demodulator channelOut_timeSync = [y(filtDelays+1:end,:); zeros(filtDelays, 1)]/sqrt(ntx); demodOut = (1/sqrt(Nfft))*ofdmdemod(channelOut_timeSync,Nfft,CPLength,CPLength/2); % Frequency domain channel equalizer Nre = size(demodOut,1); Nsymbols = size(hfreq,2); hestc = reshape(hfreq,Nre*Nsymbols,ntx,1); eqOut = ofdmEqualize(demodOut,sum(hestc,2)); % Run AE decoder dHat = helperAEWOFDMDecode(eqOut,rxNet); % Compute block errors numBlockErrors = numBlockErrors + sum(d ~= dHat); %% Simulate OFDM link with convolutional channel code % Run convolutional coded OFDM TX dataIn = randi([0 1],symbolsPerFrame*k*codeRate,1); dataEnc = convenc(dataIn(:), trellis); xqamCoded = qammod(dataEnc,M,InputType="bit",UnitAveragePower=true); xConvCoded = sqrt(Nfft).*ofdmmod(xqamCoded,Nfft,CPLength); % Broadcast transmitted symbols power over all transmit antennas channelInput_CC = sqrt(ntx).*repmat(xConvCoded, [1 ntx]); % FIlter through the fading channel [channelOutConv, pathgainsConv] = channel2(channelInput_CC); % channelOutConv is Ns x Nr, pathgainsConv is Ns x Np x Nt x Nr channelInfo2 = info(channel2); filtTaps2 = channelInfo2.ChannelFilterCoefficients; filtDelays2 = channelInfo2.ChannelFilterDelay; % Add AWGN sigPower = sum(abs(channelInput_CC(:)).^2)/numel(channelInput_CC); sigPowerdB = 10*log10(sigPower); yConvCoded = awgn(channelOutConv,snr,sigPowerdB); % Perfect channel estimator hfreqConv = ofdmChannelResponse(pathgainsConv,filtTaps2,Nfft,CPLength,... 1:Nfft,filtDelays2); % hfreqConv is Nsc x Nsym x Nt x Nr hfreqConv = reshape(hfreqConv,Nfft,[],ntx,1); % OFDM demodulator channelOut_timeSync = [yConvCoded(filtDelays2+1:end,:); zeros(filtDelays2, 1)]/sqrt(ntx);% Normalize received symbol power demodOutConv = (1/sqrt(Nfft))*ofdmdemod(channelOut_timeSync,Nfft,CPLength,CPLength/2); % Frequency domain channel equalizer NsymbolsConv = size(hfreqConv,2); hestcConv = reshape(hfreqConv, Nre*NsymbolsConv,ntx,1); eqOutConv = ofdmEqualize(demodOutConv,sum(hestcConv,2)); % Demodulate equalized symbols demodSig = qamdemod(eqOutConv,M,UnitAveragePower=true,... OutputType="bit"); dataOut = vitdec(demodSig,trellis,traceBack,"cont","hard"); % Compute error rate per block convRxdataShiftedIn = dataIn(1:end-traceBack); convRxdataShiftedOut = dataOut(traceBack+1:end); convRxSymIn = reshape(convRxdataShiftedIn,k,[]); convRxSymOut = reshape(convRxdataShiftedOut,k,[]); numConvBlockErrors = numConvBlockErrors +... sum(any(convRxSymIn ~= convRxSymOut,1)); errorstats(snrIdx, :) = errorRate(dataIn,dataOut); frameCnt = frameCnt + 1; end BLER(snrIdx,:) = [numBlockErrors numConvBlockErrors]./(frameCnt*symbolsPerFrame); end
Simulating for SNR = 0 Simulating for SNR = 2 Simulating for SNR = 4 Simulating for SNR = 6 Simulating for SNR = 8 Simulating for SNR = 10 Simulating for SNR = 12
Compare the BLER of the deep learning based autoencoder to that of the convolutional code with constraint length 7. For n = 8, the autoencoder achieves higher coding gain than the convolutional code with Viterbi decoder with the selected parameters.
figure semilogy(snrVec,BLER,"-*") grid on xlabel("SNR (dB)") ylabel("BLER") legend(sprintf("AE-OFDM (%d,%d)",n,k),sprintf("CC-OFDM (%d,%d)",n,k))

Conclusions and Further Exploration
The BLER results show that by inserting the expert knowledge in the form of OFDM modulation and demodulation to the neural network, an OFDM-based autoencoder can be trained. By allowing for multiple channel uses per input symbol ( ), the autoencoder can learn to obtain coding gain better than the conventional convolutional code with Viterbi decoder.
Change , , , , and normalization to train different autoencoders. Try different training values to optimize the training performance. See the help for the helperAEWTrainOFDMAutoencoder function and the helperAEWOFDMAutoencoderBLER function.
The results are obtained using the following default settings for training and BLER simulations:
netParams.n = 8; netParams.k = 4; netParams.normalization = "Average power"; netParams.fs = 240*1e3*128/0.85; netParams.minSNR = 0; netParams.maxSNR = 12; netParams.nfft = 128; netParams.cplen = 12; netParams.ntx = 2; trainParams.InitialLearnRate = 0.002; trainParams.MiniBatchSize= 1000; trainParams.MaxEpochs = 100; trainParams.OutputNetwork = "best-validation-loss"; trainParams.Shuffle = "every-epoch"; trainParams.LearnRateSchedule = "piecewise"; trainParams.LearnRateDropPeriod = 20; trainParams.LearnRateDropFactor = 0.8; trainParams.Plots = "none"; trainParams.Verbose = true; trainParams.InputDataFormats="CTB"; trainParams.TargetDataFormats="CTB"; simParams.SNRVec = 2:2:12; simParams.TxAntennas = 4; simParams.MinNumErrors = 100; simParams.MaxNumFrames = 1000; simParams.MaxDopplerShift = 5; simParams.FadingDelayProfile = 'A'; simParams.DelaySpread = 100; simParams.Nfft = 128; simParams.CPLength = 12; simParams.SubcarrierSpacing = 240*1e3;
Vary these parameters to train different autoencoders and test their BLER performance. Experiment with different , , normalization, and values.
List of Helper Functions
helperAEWOFDMNormalizationLayer.mhelperAEWOFDMModLayer.mhelperAEWOFDMChannelLayer.mhelperAEWOFDMChanResponseLayer.mhelperAEWOFDMDemodLayer.mhelperAEWOFDMEqualizeLayer.mhelperAEWOFDMEncode.mhelperAEWOFDMDecode.mhelperAEWTrainOFDMAutoencoder.mhelperAEWOFDMAutoencoderBLER.m
References
[1] T. O’Shea and J. Hoydis, "An Introduction to Deep Learning for the Physical Layer," in IEEE Transactions on Cognitive Communications and Networking, vol. 3, no. 4, pp. 563-575, Dec. 2017, doi: 10.1109/TCCN.2017.2758370.
[2] Lin B, Wang X, Yuan W, Wu N., "A novel OFDM autoencoder featuring CNN-based channel estimation for internet of vessels," in IEEE Internet of Things Journal, vol. 7, no. 8, pp. 7601-7611, Apr. 2020.
See Also
ofdmmod | ofdmdemod | sequenceInputLayer (Deep Learning Toolbox) | fullyConnectedLayer (Deep Learning Toolbox) | reluLayer (Deep Learning Toolbox) | softmaxLayer (Deep Learning Toolbox)
Topics
- Autoencoders for Wireless Communications
- CSI Feedback with Autoencoders
- Deep Learning in MATLAB (Deep Learning Toolbox)