raypl
Path loss and phase change for RF propagation ray
Description
[
returns the path loss and phase shift for the specified RF propagation ray. The function
calculates the path loss and phase shift using free space loss and reflection loss derived
from the propagation path, reflection materials, and antenna polarizations.pl,phase] = raypl(ray)
By default, the raypl function assumes the antennas are
unpolarized. You can polarize the antennas by specifying the
TransmitterPolarization and ReceiverPolarization
name-value arguments.
For more information about the path loss computations, see Path Loss Computation.
[
specifies options using name-value arguments. For example,
pl,phase] = raypl(ray,Name=Value)ReflectionMaterials="brick" specifies the reflection material as
brick.
Examples
Change the reflection materials and frequency for a ray, and then reevaluate the path loss and phase shift.
Launch Site Viewer with buildings in Hong Kong. For more information about the OpenStreetMap® file, see [1].
viewer = siteviewer(Buildings="hongkong.osm");Create transmitter and receiver sites.
tx = txsite(Latitude=22.2789,Longitude=114.1625, ... AntennaHeight=10,TransmitterPower=5, ... TransmitterFrequency=28e9); rx = rxsite(Latitude=22.2799,Longitude=114.1617, ... AntennaHeight=1);
Create a ray tracing propagation model, which MATLAB® represents using a RayTracing object. Configure the model to use the image method and to find paths with up to 2 surface reflections. Then, perform the ray tracing analysis.
pm = propagationModel("raytracing", ... Method="image", ... MaxNumReflections=2); rays = raytrace(tx,rx,pm);
Find the first ray with two path reflections. Then, display the properties of the ray object.
idx = find([rays{1}.NumInteractions] == 2,1);
ray = rays{1}(idx)ray =
Ray with properties:
PathSpecification: 'Locations'
CoordinateSystem: 'Geographic'
TransmitterLocation: [3×1 double]
ReceiverLocation: [3×1 double]
LineOfSight: 0
Interactions: [1×2 struct]
Frequency: 2.8000e+10
PathLossSource: 'Custom'
PathLoss: 121.8592
PhaseShift: 4.5605
Read-only properties:
PropagationDelay: 8.3060e-07
PropagationDistance: 249.0068
AngleOfDeparture: [2×1 double]
AngleOfArrival: [2×1 double]
NumInteractions: 2
Display the ray in Site Viewer.
plot(ray)
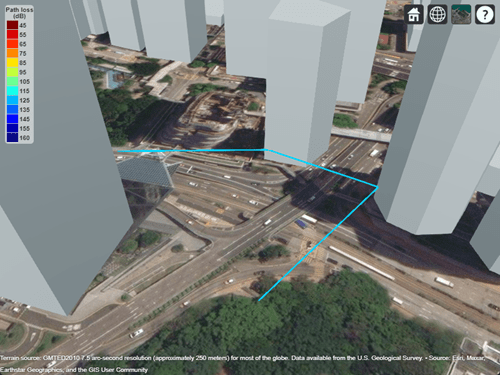
By default, the model uses concrete for the terrain material and uses building materials derived from the OpenStreetMap file. When the OpenStreetMap file does not specify materials, the model uses concrete. In this case, the ray encounters concrete as the material. You can find the interaction materials by querying the Interactions property of the ray object.
ray.Interactions.MaterialName
ans = "concrete"
ans = "concrete"
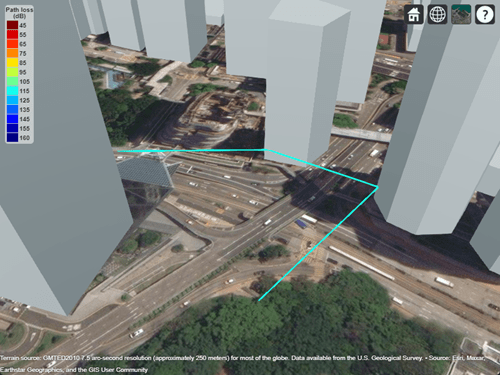
You can calculate the path loss for different materials by using the raypl function. For this example, use metal for the first reflection and glass for the second reflection.
[ray.PathLoss,ray.PhaseShift] = raypl(ray,ReflectionMaterials=["metal","glass"]); ray
ray =
Ray with properties:
PathSpecification: 'Locations'
CoordinateSystem: 'Geographic'
TransmitterLocation: [3×1 double]
ReceiverLocation: [3×1 double]
LineOfSight: 0
Interactions: [1×2 struct]
Frequency: 2.8000e+10
PathLossSource: 'Custom'
PathLoss: 114.9541
PhaseShift: 4.5605
Read-only properties:
PropagationDelay: 8.3060e-07
PropagationDistance: 249.0068
AngleOfDeparture: [2×1 double]
AngleOfArrival: [2×1 double]
NumInteractions: 2
Display the recalculated ray. The slight change in color indicates the change in path loss.
plot(ray)
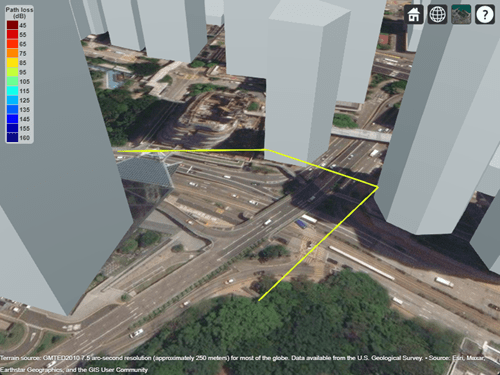
Change the frequency of the ray. Then, recalculate the path loss and phase shift. Display the ray again and observe the color change.
ray.Frequency = 2e9; [ray.PathLoss,ray.PhaseShift] = raypl(ray,ReflectionMaterials=["metal","glass"]); plot(ray)
Appendix
[1] The OpenStreetMap file is downloaded from https://www.openstreetmap.org, which provides access to crowd-sourced map data all over the world. The data is licensed under the Open Data Commons Open Database License (ODbL), https://opendatacommons.org/licenses/odbl/.
Input Arguments
RF propagation ray, specified as a comm.Ray object. The
PathSpecification property of the object must be
"Locations". All interactions in the
Interactions property of the ray must be of type
"Reflection".
Data Types: comm.Ray
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: raypl(ray,TransmitterPolarization="H",ReceiverPolarization="H"),
specifies the horizontal polarizations for the transmit and receive antennas for
ray.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: raypl(ray,"TransmitterPolarization","H","ReceiverPolarization","H"),
specifies the horizontal polarizations for the transmit and receive antennas for
ray.
Reflection materials for a non-line-of-sight (NLOS) ray, specified as a string
scalar, a 1-by-NR string vector, a character vector, a
1-by-NR cell array of character vectors, a 2-by-1 numeric vector,
or a 2-by-NR numeric matrix. NR is the number of
reflections stored in ray.
When you specify one reflection material, the reflection material applies to all
the reflections. When you specify multiple reflection materials, each material applies
to the associated reflection point in ray.
To use predefined reflection materials, specify
ReflectionMaterialsas a string scalar, a character vector, a string vector, or a cell array of character vectors. Specify each reflection material as one of these options:"concrete"— Concrete"plasterboard"— Plasterboard"ceiling-board"— Ceiling board"chipboard"— Chipboard"floorboard"— Floorboard"brick"— Brick"wood"— Wood"glass"— Glass"metal"— Metal"marble"— Marble (since R2024a)"plywood"— Plywood (since R2024a)"water"— Water"vegetation"— Vegetation"loam"— Loam"perfect-reflector"— Perfect electrical conductor
To use custom reflection materials, specify a 2-by-1 numeric vector or a 2-by-NR numeric matrix. Each column is of the form
[rp; cv], whererpis the relative permittivity andcvis the conductivity.
For more information, see Permittivity and Conductivity Values for Common Materials.
Example: ReflectionMaterials=["concrete","water"], specifies
that a ray with two reflections uses the electrical characteristics of concrete at the
first reflection point and water at the second reflection point.
Data Types: string | char | double
Transmit antenna polarization type, specified as one of these values:
"none"— Unpolarized"V"— Linearly polarized in the vertical (θ) direction"H"— Linearly polarized in the horizontal (φ) direction"LHCP"— Left-hand circular polarized"RHCP"— Right-hand circular polarizedA normalized 2-by-1 Jones vector (also called a polarization matrix) of the form
[H;V], whereHis the horizontal component andVis the vertical component.
For more information about polarization types and Jones vectors, see Jones Vector Notation.
Example: TransmitterPolarization="RHCP" specifies right-hand
circular polarization for the transmit antenna.
Data Types: double | char | string
Receive antenna polarization type, specified as one of these values:
"none"— Unpolarized"V"— Linearly polarized in the vertical (θ) direction"H"— Linearly polarized in the horizontal (φ) direction"LHCP"— Left-hand circular polarized"RHCP"— Right-hand circular polarizedA normalized 2-by-1 Jones vector (also called a polarization matrix) of the form
[H;V], whereHis the horizontal component andVis the vertical component.
For more information about polarization types and Jones vectors, see Jones Vector Notation.
Example: ReceiverPolarization=[1;0] specifies horizontal
polarization for the receive antenna by using Jones vector notation.
Data Types: double | char | string
Orientation of the transmit antenna axes, specified as a 3-by-3 unitary matrix
indicating the rotation from the transmitter local coordinate system (LCS) into the
global coordinate system (GCS). When the CoordinateSystem property
of the comm.Ray is set to
"Geographic", the GCS orientation is the local East-North-Up
(ENU) coordinate system at transmitter. For more information, see Coordinate System Orientation.
Example: TransmitterAxes=eye(3), specifies that the local
coordinate system for the transmitter axes is aligned with the global coordinate
system. This is the default orientation.
Data Types: double
Orientation of the receive antenna axes, specified as a 3-by-3 unitary matrix
indicating the rotation from the receiver local coordinate system (LCS) into the
global coordinate system (GCS). The GCS orientation is the local East-North-Up (ENU)
coordinate system at receiver when the CoordinateSystem property of
the comm.Ray is set to
"Geographic". For more information, see Coordinate System Orientation.
Example: ReceiverAxes=[0 -1 0; 1 0 0; 0 0 1], specifies a 90°
rotation around the z-axis of the local receiver coordinate system
with respect to the global coordinate system.
Data Types: double
Output Arguments
Path loss in dB, returned as a nonnegative scalar.
Data Types: double
Phase shift in radians, returned as a scalar in the range [–π, π] radians. The argument uses the e-iωt time convention.
Data Types: double
More About
The raypl function uses the methods and equations
in International Telecommunications Union Recommendations (ITU-R) P.2040-3 [2] and ITU-R P.527-5 through ITU-R
P.527-6 [3] to calculate the relative
permittivity and conductivity for common materials.
For information about the values computed for building materials specified in ITU-R P.2040, see
buildingMaterialPermittivity.For information about the values computed for terrain materials specified in ITU-R P.527, see
earthSurfacePermittivity.
The function uses the constant values that are recommended by the 2022 Committee on Data of the International Science Council (CODATA) adjustment of fundamental constants [4].
This image shows the orientation of the electromagnetic fields in the global coordinate system (GCS) and the local coordinate systems of the transmitter and receiver.
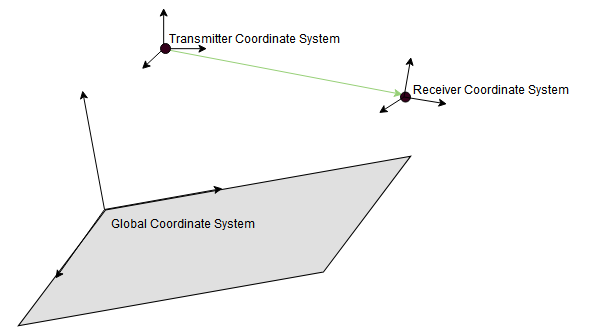
When the CoordinateSystem property of the comm.Ray is set to
"Geographic", the GCS orientation is the local East-North-Up (ENU)
coordinate system at observer. The path loss computation accounts for the round-earth
differences between ENU coordinates at the transmitter and receiver.
The ray tracing model used by the raypl function calculates
reflection losses by tracking the horizontal and vertical polarizations of signals through
the propagation path. Total power loss is the sum of free space loss and reflection
loss.
This image shows a reflection path from a transmitter site tx to a receiver site rx.
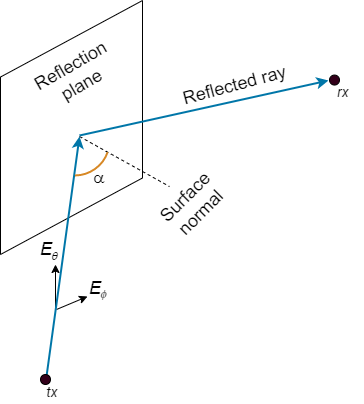
The model determines polarization and reflection loss using these steps.
Track the propagation of the ray in 3-D space by calculating the propagation matrix P. The matrix is a repeating product, where i is the number of reflection points.
For each reflection, calculate Pi by transforming the global coordinates of the incident electromagnetic field into the local coordinates of the reflection plane, multiplying the result by a reflection coefficient matrix, and transforming the coordinates back into the original global coordinate system [1]. The equations for Pi and P0 are:
where:
s, p, and k form a basis for the plane of incidence (the plane created by the incident ray and the surface normal of the reflection plane). s and p are perpendicular and parallel, respectively, to the plane of incidence.
kin and kout are the directions (in global coordinates) of the incident and exiting rays, respectively.
sin and sout are the directions (in global coordinates) of the horizontal polarizations for the incident and exiting rays, respectively.
pin and pout are the directions (in global coordinates) of the vertical polarizations for the incident and exiting rays, respectively.
RH and RV are the Fresnel reflection coefficients for the horizontal and vertical polarizations, respectively. α is the incident angle of the ray and εr is the complex relative permittivity of the material.
Project the propagation matrix P into a 2-by-2 polarization matrix R. The model rotates the coordinate systems for the transmitter and receiver so that they are in global coordinates.
where:
Hrx and Vrx are the directions (in global coordinates) of the horizontal (Eθ) and vertical (Eϕ) polarizations, respectively, for the receiver.
Hin and Vin are the directions (in global coordinates) of the propagated horizontal and vertical polarizations, respectively.
Vtx is the direction (in global coordinates) of the nominal vertical polarization for the ray departing the transmitter.
ktx is the direction (in global coordinates) of the ray departing the transmitter.
Specify the normalized horizontal and vertical polarizations of the electric field at the transmitter and receiver by using the 2-by-1 Jones polarization vectors Jtx and Jrx, respectively. If either the transmitter or receiver are unpolarized, then the model assumes .
Calculate the polarization and reflection loss IL by combining R, Jtx, and Jrx.
For Jones vector notation, the raypl function describes signal polarization using Jones calculus.
The orthogonal components of Jones vectors are defined for Eθ and Eφ. This table shows the Jones vector corresponding to various antenna polarizations.
| Antenna Polarization Type | Corresponding Jones Vector |
|---|---|
Linear polarized in the θ direction |
|
Linear polarized in the φ direction |
|
Left-hand circular polarized (LHCP) |
|
Right-hand circular polarized (RHCP) |
|
References
[1] Chipman, Russell A., Garam Young, and Wai Sze Tiffany Lam. "Fresnel Equations." In Polarized Light and Optical Systems. Optical Sciences and Applications of Light. Boca Raton: Taylor & Francis, CRC Press, 2019.
[2] International Telecommunications Union Radiocommunication Sector. Effects of Building Materials and Structures on Radiowave Propagation Above About 100MHz. Recommendation P.2040. ITU-R, approved August 23, 2023. https://www.itu.int/rec/R-REC-P.2040/en.
[3] International Telecommunications Union Radiocommunication Sector. Electrical Characteristics of the Surface of the Earth. Recommendation P.527. ITU-R, approved September 27, 2021. https://www.itu.int/rec/R-REC-P.527/en.
[4] Mohr, Peter J., Eite Tiesinga, David B. Newell, and Barry N. Taylor. “Codata Internationally Recommended 2022 Values of the Fundamental Physical Constants.” NIST, May 8, 2024. https://www.nist.gov/publications/codata-internationally-recommended-2022-values-fundamental-physical-constants.
Extended Capabilities
Usage notes and limitations:
When you specify multiple reflective materials, you must define each value as a
character vector (char data type) in a cell array.
Version History
Introduced in R2020aThe raypl function models materials using the constant values
that are recommended by the 2022 Committee on Data of the International Science Council
(CODATA) adjustment of fundamental constants [4].
In previous releases, the function used constant values from ITU-R P.2040 and P.527. As
a result of this change, the raypl function can return different
values in R2025a compared to previous releases.
The raypl function models materials using the methods and equations
in ITU-R P.2040-3 and ITU-R P.527-5 through ITU-R P.527-6.
In previous releases, the function used ITU-R P.2040-1. As a result of these changes,
the raypl function can return different values in R2024a compared to
previous releases.
Specify the reflection materials as marble or plywood by using the
ReflectionMaterials name-value argument and specifying
"marble" or "plywood" as input.
When you find propagation paths using the raytrace function and a
ray tracing model that uses the shooting and bouncing rays (SBR) method, MATLAB® corrects the results so that the geometric accuracy of each path is exact,
using single-precision floating-point computations. In previous releases, the paths have
approximate geometric accuracy.
As a result, when you use rays returned by the raytrace function as
input to the raypl function, the raypl function
can return different results than in previous releases.
See Also
Functions
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)