M-PSK Demodulator Baseband

Demodulate PSK-modulated data

• 

Libraries:
Communications Toolbox / Modulation / Digital Baseband Modulation / PSK
Communications Toolbox HDL Support / Modulation / PM

Description

The M-PSK Demodulator Baseband block demodulates a baseband representation of a PSK-modulated signal. The modulation order, M, is equivalent to the number of points in the signal constellation and is determined by the M-ary number parameter. The block accepts scalar or column vector input signals.

Examples

Modulate and Demodulate 8-PSK Signal

Generate and demodulate a noisy 8-PSK signal.

Open the doc_8psk_model model. The model generates random data using the Random Integer Generator block. To modulate the random data, the model uses the M-PSK Modulator Baseband block with a modulation order of 8 and a constellation order set to Gray. Subsequently, the modulated data passes through an additive white Gaussian noise channel (AWGN Channel block). The model displays the noisy constellation through the Constellation Diagram block. To demodulate this noisy signal, it employs the M-PSK Demodulator Baseband block with the same modulation and constellation order as the modulator. Finally, the model computes the error statistics using the Error Rate Calculation.

Run the model.

Collect the error statistics in a vector, ErrorVec. Observe that the number of symbol errors is zero when Eb/No is 15 dB.

Number of symbol errors = 0

Change the Eb/No of the AWGN Channel block from 15 dB to 5 dB. The constellation diagram shows the increase in the noise.

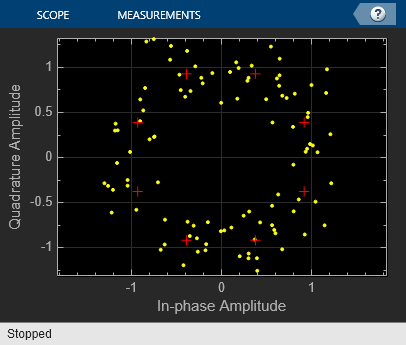
Because of the increase in the noise level, the number of symbol errors is greater than zero.

Number of symbol errors = 21

Gray-Coded M-PSK Modulation Error Rate in AWGN Channel Using Simulink

This example uses the doc_gray_code to compute bit error rates (BER) and symbol error rates (SER) for M-PSK modulation. The theoretical error rate performance of M-PSK modulation in AWGN is compared to the error rate performance for Gray-coded symbol mapping and to the error rate performance of binary-coded symbol mapping.

The Random Integer Generator block serves as the source, producing a sequence of integers. The Integer to Bit Converter block converts each integer into a corresponding binary representation. The M-PSK Modulator Baseband block in the doc_gray_code model:

• Accepts binary-valued inputs that represent integers in the range [0, (M - 1], where M is the modulation order.

• Maps binary representations to constellation points using a Gray-coded ordering.

• Produces unit-magnitude complex phasor outputs, with evenly spaced phases in the range [0, (2 (M - 1) / M)].

The AWGN Channel block adds white Gaussian noise to the modulated data. The M-PSK Demodulator Baseband block demodulates the noisy data. The Bit to Integer Converter block converts each binary representation to a corresponding integer. Then two separate Error Rate Calculation blocks calculate the error rates of the demodulated data. The block labeled SER Calculation compares the integer data to compute the symbol error rate statistics and the block labeled BER Calculation compares the bits data to compute the bit error rate statistics. The output of the Error Rate Calculation block is a three-element vector containing the calculated error rate, the number of errors observed, and the amount of data processed.

To reduce simulation run time and ensure that the statistics of the errors remain stable as the Eb/N0 ratio increases, the model is configured to run until 100 errors occur or until 1e8 bits have been transmitted.

The model initializes variables used to configure block parameters by using the PreLoadFcn callback function. For more information, see Model Callbacks (Simulink).

Produce Error Rate Curves

Compute the theoretical BER for nondifferential 8-PSK in AWGN over a range of Eb/N0 values by using the berawgn function. Simulate the doc_gray_code model with Gray-coded symbol mapping over the same range of Eb/N0 values.

Compare Gray coding with binary coding, by modifying the M-PSK Modulator Baseband and M-PSK Demodulator Baseband blocks to set the Constellation ordering parameter to Binary instead of Gray. Simulate the doc_gray_code model with binary-coded symbol mapping over the same range of Eb/N0 values.

Plot the results by using the semilogy function. The Gray-coded system achieves better error rate performance than the binary-coded system. Further, the Gray-coded error rate aligns with the theoretical error rate statistics.

Ports

Input

In — Input signal

scalar | vector

Input port accepting a baseband representation of a PSK-modulated signal.

This port in unnamed on the block until you enable the Var port.

Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean

Var — Noise variance estimate

positive scalar

Noise variance estimate, specified as a positive scalar.

Note

The exact LLR algorithm computes exponentials using finite precision arithmetic. For computations involving very large positive or negative magnitudes, the exact LLR algorithm yields:

• Inf or -Inf if the noise variance is a very large value

• NaN if the noise variance and signal power are both very small values

The approximate LLR algorithm does not compute exponentials. You can avoid Inf, -Inf, and NaN results by using the approximate LLR algorithm.

Dependencies

This parameter applies when you set Noise variance source to Port.

Data Types: double | single

Output

Out — Output signal

scalar | vector

Output signal, returned as a scalar or vector. The output is a demodulated version of the PSK-modulated signal.

Data Types: single | double | fixed point

Parameters

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Main

M-ary number — Modulation order of the PSK constellation

8 (default) | scalar

Specify the modulation order as a positive integer power of two.

Example: 2 | 16

Output type — Output signal data type

Integer (default) | Bit

Specify the elements of the input signal as integers or bits. If Output type is Bit, the number of samples per frame is an integer multiple of the number of bits per symbol, log₂(M).

Decision type — Demodulator output

Hard decision (default) | Log-likelihood ratio | Approximate log-likelihood ratio

Specify the demodulator output to be hard decision, log-likelihood ratio (LLR), or approximate LLR. The LLR and approximate LLR outputs are used with error decoders that support soft-decision inputs such as a Viterbi Decoder, to achieve superior performance. For more information, see Algorithms.

The output values for Log-likelihood ratio and Approximate log-likelihood ratio decision types are of the same data type as the input values.

Dependencies

This parameter applies when you set Output type to Bit.

Noise variance source — Source of noise variance estimate

Dialog (default) | Port

Source of noise variance estimate, specified as one of these options.

• Set this parameter to Dialog to define the noise variance by using the Noise variance parameter.

• Set this parameter to Port to define the noise variance by using the Var port.

Specify the source of the noise variance estimate.

• To specify the noise variance from the dialog box, select Dialog.

• To input the noise variance from an input port, select Port.

Dependencies

This parameter applies when you set Decision type to Log-likelihood ratio or Approximate log-likelihood ratio.

Noise variance — Estimate of noise variance

1 (default) | positive scalar

Specify the estimate of the noise variance as a positive scalar.

This parameter is tunable in all simulation modes. If you use the Simulink Coder™ rapid simulation (RSIM) target to build an RSIM executable, then you can tune the parameter without recompiling the model. Avoiding recompilation is useful for Monte Carlo simulations in which you run the simulation multiple times (perhaps on multiple computers) with different amounts of noise.

Note

The exact LLR algorithm computes exponentials using finite precision arithmetic. For computations involving very large positive or negative magnitudes, the exact LLR algorithm yields:

• Inf or -Inf if the noise variance is a very large value

• NaN if the noise variance and signal power are both very small values

The approximate LLR algorithm does not compute exponentials. You can avoid Inf, -Inf, and NaN results by using the approximate LLR algorithm.

Tunable: Yes

Dependencies

This parameter applies when you set Noise variance source to Dialog.

Constellation ordering — Symbol mapping

Gray (default) | Binary | User-defined

Specify how the integer or group of log₂(M) bits is mapped to the corresponding symbol.

• When you set Constellation ordering to Gray, the output symbol is mapped to the input signal using a Gray-encoded signal constellation.

• When you set Constellation ordering to Binary, the modulated symbol is e^j(ϕ+2πm/M), where ϕ is the phase offset in radians, m is the integer output such that 0 ≤ m ≤ M – 1, and M is the modulation order.

• When you set Constellation ordering to User-defined, specify a vector of size M, which has unique integer values in the range [0, M–1]. The first element of this vector corresponds to the constellation point having a value of e^jϕ with subsequent elements running counterclockwise.

Example: [0 3 2 1] for a QPSK constellation.

Constellation mapping — User-defined symbol mapping

[0:7] (default) | vector

Specify the order in which input integers are mapped to output integers. The parameter is available when Constellation ordering is User-defined, and must be a row or column vector of size M having unique integer values in the range [0, M – 1].

The first element of this vector corresponds to the constellation point at (0 + ϕ) angle, with subsequent elements running counterclockwise. The last element corresponds to the (–2π/M + ϕ) constellation point. ϕ is the phase offset in radians (Phase offset (rad)) and M is the modulation order (M-ary number).

Dependencies

This parameter applies when you set Constellation ordering to User-defined.

Phase offset (rad) — Phase offset in radians

pi/8 (default) | scalar

Phase offset of the initial constellation in radians, specified as a scalar.

Example: pi/4

Data Types

Output data type — Output data type

Inherit via internal rule (default) | Smallest unsigned integer | double | single | int8 | uint8 | int16 | uint16 | int32 | uint32

Specify the data type of the demodulated output signal.

For information about specifying data types, see Data Type Assistant.

Block Characteristics

Data Types	Boolean | double | fixed pointa, b, c | integer | single
Multidimensional Signals	no
Variable-Size Signals	yes
a M = 2, 4, 8 only. b Fixed-point inputs must be signed. c When ASIC/FPGA is selected in the Hardware Implementation Pane, output is ufix(1) for bit outputs, and ufix(ceil(log2(M))) for integer outputs.

More About

Data Type Assistant

The Data Type Assistant helps you set data attributes. To use the Data Type Assistant, click . For more information, see Specify Data Types Using Data Type Assistant (Simulink).

Algorithms

Hard-Decision BPSK Demodulation

The signal preprocessing required for BPSK demodulation depends on the configuration.

This figure shows the hard-decision BPSK demodulation signal diagram for the trivial phase offset (multiple of π/2) configuration.

This figure shows the hard-decision BPSK demodulation floating-point signal diagram for the nontrivial phase offset configuration.

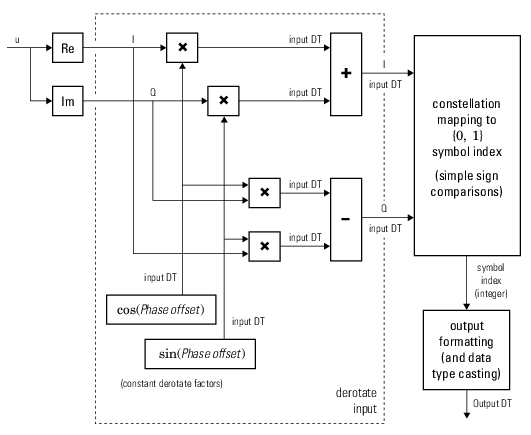
This figure shows the hard-decision BPSK demodulation fixed-point signal diagram for the nontrivial phase offset configuration.

Hard-Decision QPSK Demodulation

The signal preprocessing required for QPSK demodulation depends on the configuration.

This figure shows the hard-decision QPSK demodulation signal diagram for the trivial phase offset (odd multiple of π/4) configuration.

This figure shows the hard-decision QPSK demodulation floating-point signal diagram for the nontrivial phase offset configuration.

This figure shows the hard-decision QPSK demodulation fixed-point signal diagram for the nontrivial phase offset configuration.

Hard-Decision Higher-Order PSK

The signal preprocessing required for higher order PSK demodulation depends on the configuration.

This figure shows the hard-decision 8-PSK demodulation signal diagram for the trivial phase offset (odd multiple of π/8) configuration.

This figure shows the hard-decision 8-PSK demodulation fixed-point signal diagram for trivial phase offset (odd multiple of π/8) configuration.

This figure shows the hard-decision M-PSK demodulation floating-point signal diagram for the nontrivial phase offset configuration.

For M > 8, to improve speed and implementation costs, no derotation arithmetic is performed for trivial case (specifically, when phase offset is 0, π/2, π, or 3π/2).

Also, for M > 8, only double and single input types are supported.

Log-Likelihood Ratio and Approximate Log-Likelihood Ratio

The exact LLR and approximate LLR algorithms (soft-decision) are described in Phase Modulation.

References

[1] Proakis, John G. Digital Communications. 4th ed. New York: McGraw Hill, 2001.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).

Version History

Introduced before R2006a