Linear Equalizer
Equalize modulated signals using linear filtering
Libraries:
Communications Toolbox /
Equalizers
Description
The Linear Equalizer block uses a tapped delay line filter to equalize a linearly modulated signal through a dispersive channel. Using an estimate of the channel modeled as a finite input response (FIR) filter, the block processes input frames and outputs the estimated signal.
This icon shows the block with all ports enabled for configurations that use the LMS or RLS adaptive algorithm.
![]()
This icon shows the block with all ports enabled for configurations that use the CMA adaptive algorithm.
![]()
Examples
Apply linear equalization using the least mean squares (LMS) algorithm to recover QPSK symbols passed through an AWGN channel.
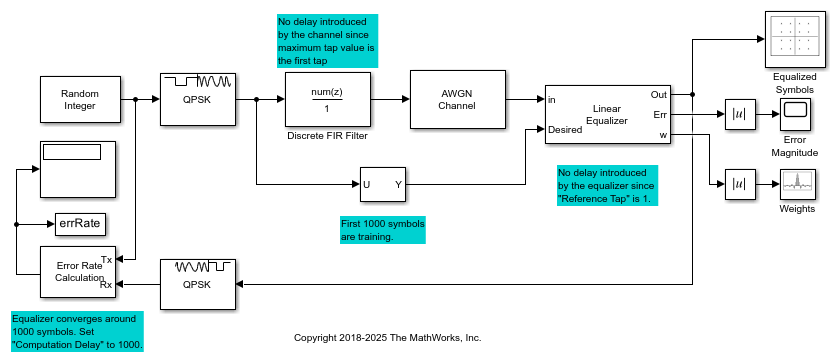
The slex_lineq_qpsk_signal model generates an M=4 sequence using the Random Integer Generator block. The sequence is modulated with the M-PSK Modulator Baseband block, filtered with the Discrete FIR Filter block, and then impaired with the AWGN block. The Linear Equalizer block equalizes the data sequence, the data is demodulated with the M-PSK Demodulator Baseband block, and the bit error rate is computed. The signal path out of the modulator is split to a Selector block, which provides the first 1000 symbols of the modulated signal to the equalizer as an initial training sequence.
No delay is introduced between the transmitted and received signal because the maximum tap value is the first tap of the discrete FIR filter and the equalizer reference tap is 1. The equalizer converges after around 1000 symbols so this value is used for the computation delay of the Error Rate Calculation block.
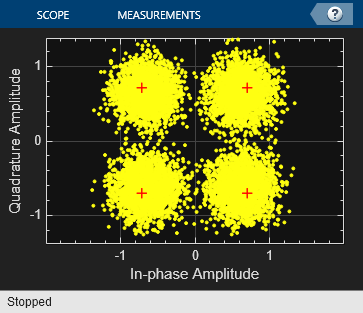
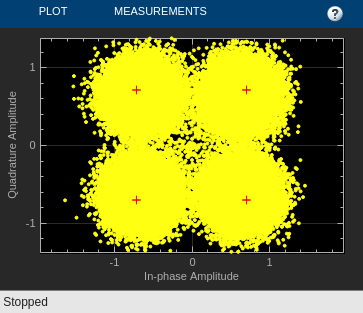
The computed error rate is displayed and plots show the equalized constellation, equalized tap weights, and signal error magnitude.
Computed error rate = 0.0021111
Extended Examples
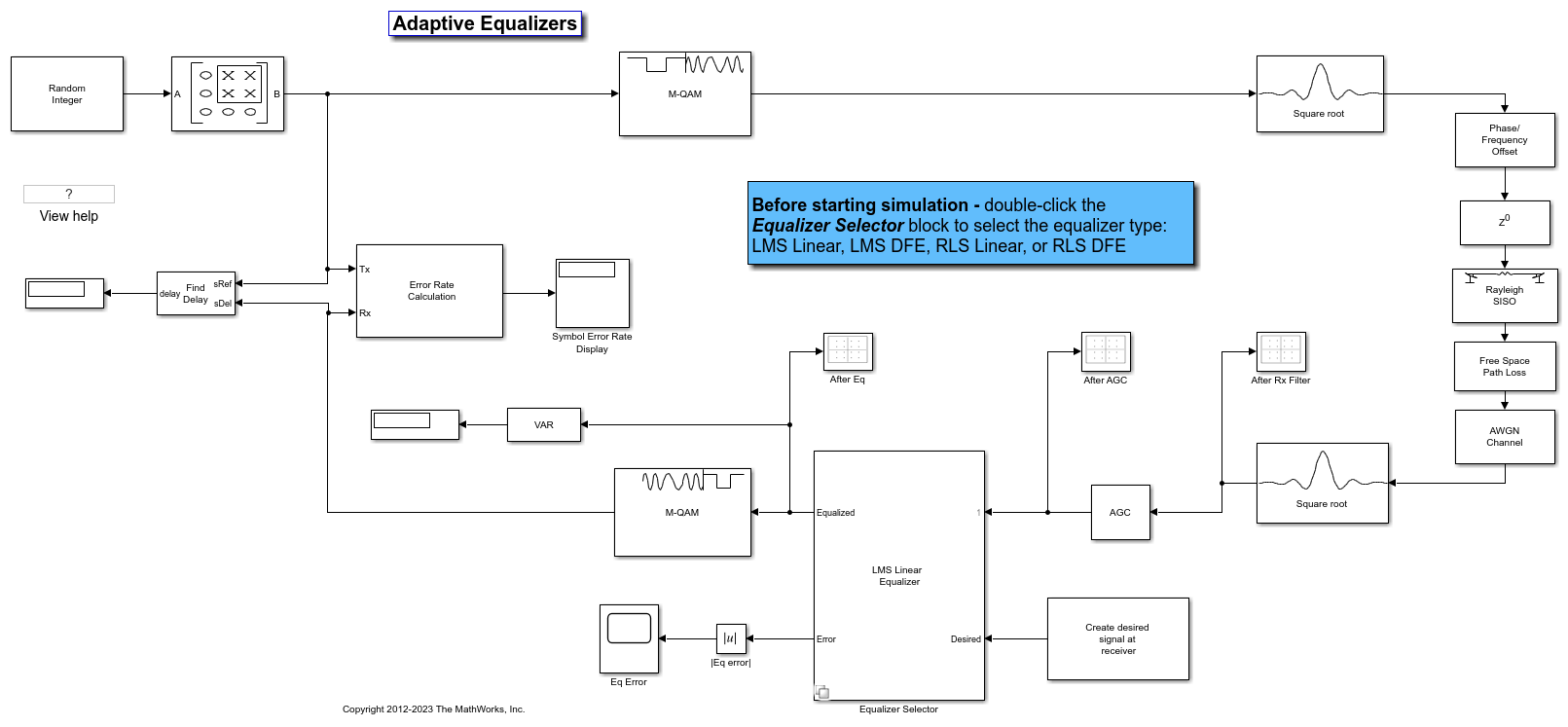
Adaptive Equalization with Filtering and Fading Channel
The behavior of the selected adaptive equalizer in a communication link that has a fading channel. The transmitter and receiver have root raised cosine pulse shaped filtering. A subsystem block enables you to select between linear or decision feedback equalizers that use the least mean square (LMS) or recursive least square (RLS) adaptive algorithm.
Ports
Input
Input signal, specified as a column vector. The vector length of in must be equal to an integer multiple of the Number of input samples per symbol parameter. For more information, see Symbol Tap Spacing.
Data Types: double
Complex Number Support: Yes
Training symbols, specified as a column vector. The vector length of
Desired must be less than or equal to the length of input in. The
Desired input port is ignored when the Train input
port is 0.
Dependencies
To enable this port, set the Adaptive
algorithm parameter to LMS or
RLS.
Data Types: double
Complex Number Support: Yes
Train equalizer flag, specified as 1 or 0.
The block starts training when this value changes from 0 to
1 (at the rising edge). The block trains until all symbols in the
Desired input
port are processed.
Dependencies
To enable this port, set the Adaptive
algorithm parameter to LMS or
RLS and select the Enable training
control input parameter.
Data Types: Boolean
Update tap weights flag, specified as 1 or
0. The tap weights are updated when this value is
1.
Dependencies
To enable this port, set the Adaptive
algorithm parameter to CMA and the
Source of adapt
weights flag parameter to Input
port.
Data Types: Boolean
Reset equalizer flag, specified as 1 or 0.
If Reset is set to 1, the block resets the tap weights
before processing the incoming signal. The block performs initial training until all
symbols in the Desired input
port are processed.
Dependencies
To enable this port, select the Enable reset input parameter.
Data Types: Boolean
Output
Equalized symbols, returned as a column vector that has the same length as input signal in.
This port is unnamed until you select the Output error signal or Output taps weights parameter.
Error signal, returned as a column vector that has the same length as input signal in.
Dependencies
To enable this port, select the Output error signal parameter.
Tap weights, returned as an NTaps-by-1 vector, where NTaps is the value of the Number of taps parameter. w contains the tap weights from the last tap weight update.
Dependencies
To enable this port, select the Output taps weights parameter.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Structure parameters
Number of equalizer taps, specified as a positive integer. The number of equalizer taps must be greater than or equal to the value of the Number of input samples per symbol parameter.
Signal constellation, specified as a vector. The default value is a QPSK
constellation generated using this code: pskmod(0:3,4,pi/4).
Number of input samples per symbol, specified as a positive integer. Setting this
parameter to any number greater than 1 effectively creates a
fractionally spaced equalizer. For more information, see Symbol Tap Spacing.
Algorithm parameters
Adaptive algorithm used for equalization, specified as one of these values:
LMS— Update the equalizer tap weights using the Least Mean Square (LMS) Algorithm.RLS— Update the equalizer tap weights using the Recursive Least Square (RLS) Algorithm.CMA— Update the equalizer tap weights using the Constant Modulus Algorithm (CMA).
Step size used by the adaptive algorithm, specified as a positive scalar. Increasing the step size reduces the equalizer convergence time but causes the equalizer output estimates to be less stable.
Tunable: Yes
Dependencies
To enable this parameter, set Adaptive
algorithm to LMS or
CMA.
Forgetting factor used by the adaptive algorithm, specified as a scalar in the range (0, 1]. Decreasing the forgetting factor reduces the equalizer convergence time but causes the equalizer output estimates to be less stable.
Tunable: Yes
Dependencies
To enable this parameter, set Adaptive
algorithm to RLS.
Initial inverse correlation matrix, specified as a scalar or an
NTaps-by-NTaps
matrix. NTaps is equal to the Number of
taps parameter value. If you specify this value as a scalar,
a, the equalizer sets the initial inverse correlation matrix to
a times the identity matrix:
a(eye(NTaps)).
Dependencies
To enable this parameter, set Adaptive
algorithm to RLS.
Control parameters
Reference tap, specified as a positive integer less than or equal to the Number of taps parameter value. The equalizer uses the reference tap location to track the main energy of the channel.
Input signal delay in samples relative to the reset time of the equalizer, specified
as a nonnegative integer. If the input signal is a vector of length greater than 1, then
the input delay is relative to the start of the input vector. If the input signal is a
scalar, then the input delay is relative to the first call of the block and to the first
call of the block after the Reset input port
toggles to 1.
Dependencies
To enable this parameter, set Adaptive
algorithm to LMS or
RLS.
Source of the adapt tap weights request, specified as one of these values:
Property— Specify this value to use the Adaptive algorithm parameter to control when the block adapts tap weights.Input port— Specify this value to use the Update input port to control when the block adapts tap weights.
Dependencies
To enable this parameter, set Adaptive
algorithm to CMA.
Select this parameter to adaptively update the equalizer tap weights. If this parameter is cleared, the block keeps the equalizer tap weights unchanged.
Dependencies
To enable this parameter, set Adaptive
algorithm to CMA and Source of adapt
weights flag to Property.
Source for initial tap weights, specified as one of these values:
Auto— Initialize the tap weights to the algorithm-specific default values, as described in the Initial weights parameter.Property— Initialize the tap weights using the Initial weights parameter value.
Initial tap weights used by the adaptive algorithm, specified as a scalar or an
NTaps-by-1 vector.
NTaps is equal to the Number of
taps parameter value. The default is 0 when the
Adaptive
algorithm parameter is set to LMS or
RLS. The default is [0;0;1;0;0] when the
Adaptive
algorithm parameter is set to CMA.
If you specify Initial weights as a vector, the vector length must be equal to the Number of taps parameter value. If you specify Initial weights as a scalar, the equalizer uses scalar expansion to create a vector of length Number of taps with all values set to Initial weights.
Dependencies
To enable this parameter, set Initial tap weights source to
Property.
Tap weight update period in symbols, specified as a positive integer. The equalizer updates the tap weights after processing this number of symbols.
Select this parameter to enable input port Train. If this parameter is cleared, the block does not reenter training mode after the initial tap training.
Dependencies
To enable this parameter, set Adaptive
algorithm to LMS or RLS.
Select this parameter to use decision directed mode to update equalizer tap weights. If this parameter is cleared, the block keeps the equalizer tap weights unchanged after training.
Dependencies
To enable this parameter, set Adaptive
algorithm to LMS or
RLS.
Select this parameter to enable input port Reset. If this parameter is cleared, the block does not reset the tap weights before processing the incoming signal.
Select Info to display linear equalizer information for applied settings.
Diagnostic parameters
Select this parameter to enable output port Err containing the equalizer error signal.
Select this parameter to enable output port w containing tap weights from the last tap weight update.
Type of simulation to run, specified as Code generation or
Interpreted execution.
Code generation— Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with theInterpreted executionoption.Interpreted execution— Simulate the model by using the MATLAB® interpreter. This option shortens startup time, but the speed of subsequent simulations is slower than with theCode generationoption. In this mode, you can debug the source code of the block.
For more information, see Interpreted Execution vs. Code Generation (Simulink).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
You can configure the equalizer to operate as a symbol-spaced equalizer or as a fractional symbol-spaced equalizer.
To operate the equalizer at a symbol-spaced rate, specify the number of samples per symbol as
1. Symbol-rate equalizers have taps spaced at the symbol duration. Symbol-rate equalizers are sensitive to timing phase.To operate the equalizer at a fractional symbol-spaced rate, specify the number of input samples per symbol as an integer greater than
1and provide an input signal oversampled at that sampling rate. Fractional symbol-spaced equalizers have taps spaced at an integer fraction of the input symbol duration. Fractional symbol-spaced equalizers are not sensitive to timing phase.
Algorithms
Linear equalizers can remove intersymbol interference (ISI) when the frequency response of a channel has no null. If a null exists in the frequency response of a channel, linear equalizers tend to enhance the noise. In this case, use decision feedback equalizers to avoid enhancing the noise.
A linear equalizer consists of a tapped delay line that stores samples from the input signal. Once per symbol period, the equalizer outputs a weighted sum of the values in the delay line and updates the weights to prepare for the next symbol period.
Linear equalizers can be symbol-spaced or fractional symbol-spaced.
For a symbol-spaced equalizer, the number of samples per symbol, K, is 1. The output sample rate equals the input sample rate.
For a fractional symbol-spaced equalizer, the number of samples per symbol, K, is an integer greater than 1. Typically, K is 4 for fractionally spaced equalizers. The output sample rate is 1/T and the input sample rate is K/T, where T is the symbol period. Tap-weight updating occurs at the output rate.
This schematic shows a linear equalizer with L weights, a symbol period of T, and K samples per symbol. If K is 1, the result is a symbol-spaced linear equalizer instead of a fractional symbol-spaced linear equalizer.

In each symbol period, the equalizer receives K input samples at the tapped delay line. The equalizer then outputs a weighted sum of the values in the tapped delay line and updates the weights to prepare for the next symbol period.
For more information, see Equalization.
For the LMS algorithm, in the previous schematic, w is a vector of all weights wi, and u is a vector of all inputs ui. Based on the current set of weights, the LMS algorithm creates the new set of weights as
wnew = wcurrent + (StepSize) ue*.
The step size used by the adaptive algorithm is specified as a positive scalar. Increasing the
step size reduces the equalizer convergence time but causes the equalized output signal to
be less stable. To determine the maximum step size allowed when using the LMS adaptive
algorithm, use the maxstep object
function. The * operator denotes the complex conjugate and the error calculation e = d -
y.
For the RLS algorithm, in the previous schematic, w is the vector of all weights wi, and u is the vector of all inputs ui. Based on the current set of inputs, u, and the inverse correlation matrix, P, the RLS algorithm first computes the Kalman gain vector, K, as
The forgetting factor used by the adaptive algorithm is specified as a scalar in the range (0, 1]. Decreasing the forgetting factor reduces the equalizer convergence time but causes the equalized output signal to be less stable. H denotes the Hermitian transpose. Based on the current inverse correlation matrix, the new inverse correlation matrix is
Based on the current set of weights, the RLS algorithm creates the new set of weights as
wnew = wcurrent+K*e.
The * operator denotes the complex conjugate and the error calculation e = d - y.
For the CMA adaptive algorithm, in the previous schematic, w is the vector of all weights wi, and u is the vector of all inputs ui. Based on the current set of weights, the CMA adaptive algorithm creates the new set of weights as
wnew = wcurrent + (StepSize) u*e.
The step size used by the adaptive algorithm is specified as a positive scalar. Increasing the
step size reduces the equalizer convergence time but causes the equalized output signal to
be less stable. To determine the maximum step size allowed by the CMA adaptive algorithm,
use the maxstep object
function. The * operator denotes the complex conjugate and the error calculation
e = y(R -
|y|2), where R is a constant related to the signal
constellation.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2019a
See Also
Blocks
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)