Binary-Input RS Encoder

Create Reed-Solomon code from binary vector data

• 

Libraries:
Communications Toolbox / Error Detection and Correction / Block

Description

The Binary-Input RS Encoder block creates a Reed-Solomon code.

The symbols for the code are binary sequences of length M, corresponding to elements of the Galois field GF(2^M). The first bit in each symbol is the most significant bit.

Suppose M = 3, N = 2³-1 = 7, and K = 2. Then a message is a vector of length 2 whose entries are integers between 0 and 7. A corresponding codeword is a vector of length 7 whose entries are integers between 0 and 7. The following figure illustrates possible input and output signals to this block when codeword length N=7 and message word length K=2. Since N=2^M–1, when N=7, the symbol length, M=3.

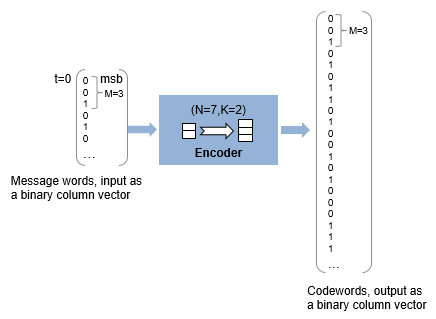
Each input message word is a binary vector of length 6, that represents 2 three-bit integers. Each corresponding output codeword is a binary vector of length 21 that represents 7 three-bit integers. For more information, see Input and Output Signal Length in RS Blocks.

Examples

Compute BER of Reed-Solomon Encoded Signal

Apply Reed-Solomon (RS) encoding and 2-FSK modulation to an integer-valued signal, pass the modulated signal through an AWGN channel. Compute the bit error rate (BER) of the signal after applying 2-FSK demodulation and binary output RS decoding.

The cm_binary_input_rs_encoder_output_decoder model includes the:

• Random Integer Generator block — To generate an integer-valued signal

• Data Type Conversion (Simulink) block — To convert data type to type expected for error rate computations

• Binary-Input RS Encoder block — To RS encode the signal

• M-FSK Modulator Baseband block — To 2-FSK-modulates the signal

• AWGN Channel block — To add Gaussian white noise to the signal

• M-FSK Demodulator Baseband block — To 2-FSK demodulate signal

• Binary-Output RS Decoder block — To RS decode the signal

• Two separate Error Rate Calculation blocks — To compute the error statistics for the signal before and after RS decoding

Compare the decoded and encoded error statistics to show error correction benefit for the received signal provided by the RS coding.

For an AWGN channel with SNR = -2 dB, the computed error rates are:
                                  Decoded     Encoded
                                  ________    _______

    BER                           0.000375    0.00235
    Number of errors                    18        141
    Number of bits transmitted       48000      60000

Ports

Input

In — Message

binary column vector

Message in bits, specified as one of the following:

• When there is no message shortening, a (N_C×K×M)-by-1 binary column vector.

• When there is message shortening, a (N_C×S×M)-by-1 binary column vector.

N_C is the number of message words, K is the Message length K (symbols), M is the number of bits per symbol, and S is the Shortened message length S (symbols).

Note

The number of decoded message words equals the number of codewords.

For more information, see Input and Output Signal Length in RS Blocks.

Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean | ufix(1)

Output

Out — Reed-Solomon codeword

binary column vector

Reed-Solomon codeword in bits, returned as an (N_C×(N – K + S – P)×M)-by-1 binary column vector. N_C is the number of codewords, N is the Codeword length N (symbols), K is the Message length K (symbols), S is the Shortened message length S (symbols), P is the number of punctures per codeword, and M is the number of bits per symbol.

For more information, see Input and Output Signal Length in RS Blocks.

Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean | ufix(1)

For more information, see Supported Data Types.

Parameters

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Codeword length N (symbols) — Codeword length

7 (default) | integer

Codeword length in symbols, specified as an integer.

For more information, see Restrictions on the M and the Codeword Length N and Input and Output Signal Length in RS Blocks.

Message length K (symbols) — Message word length

3 (default) | integer

Message word length in symbols, specified as an integer in the range [1, N–2], where N is the codeword length.

Shortened message length S (symbols) — Shortened message word length

3 (default) | integer

Shortened message word length in symbols, specified as an integer, such that S ≤ K. When Shortened message length S (symbols) < Message length K (symbols), the Reed-Solomon code is shortened.

You still specify N and K values for the full-length (N, K) code but the decoding is shortened to an (N–K+S, S) code.

Dependencies

To enable this parameter, select Specify shortened message length.

Generator polynomial — Generator polynomial

rsgenpoly(7, 3, [], [], 'double') (default) | polynomial character vector | binary row vector | binary Galois row vector

Generator polynomial with values from 0 to 2^M–1, in order of descending power, specified as one of the following:

• A polynomial character vector. For more information, see Representation of Polynomials in Communications Toolbox.

• An integer row vector that represents the coefficients of the generator polynomial in order of descending power.

• An integer Galois row vector that represents the coefficients of the generator polynomial in order of descending power.

Each coefficient is an element of the Galois field defined by the primitive polynomial. For more information, see Specify the Generator Polynomial.

Example: [1 3 1 2 3], which is equivalent to rsgenpoly(7,3)

Dependencies

To enable this parameter, select Specify generator polynomial.

Primitive polynomial — Primitive polynomial

'X^3 + X + 1' (default) | polynomial character vector | binary row vector

Primitive polynomial in order of descending power. This polynomial is of order M and defines the finite Galois field GF(2^M) corresponding to the integers that form message words and codewords. Specify the primitive polynomial as one of the following:

• A polynomial character vector. For more information, see Representation of Polynomials in Communications Toolbox.

• A binary row vector that represents the coefficients of the generator polynomial.

For more information, see Restrictions on the M and the Codeword Length N.

Example: 'X^3 + X + 1', which is the primitive polynomial used for a (7,3) code, ppoly = primpoly(3,'nodisplay'); int2bit(ppoly,ceil(log2(max(ppoly))))'

Dependencies

To enable this parameter, select Specify primitive polynomial.

Puncture vector — Puncture vector

[ones(2,1); zeros(2,1)] (default) | binary column vector

Puncture vector, specified as an (N–K)-by-1 binary column vector. Element indices with 1s represent data symbol indices that pass through the block unaltered. Element indices with 0s represent data symbol indices that get punctured, or removed, from the data stream. For more information, see Puncturing and Erasures.

Dependencies

To enable this parameter, select Puncture code.

Output data type — Output type of the block

Same as input (default) | boolean | double

Output type of the block, specified as Same as input, boolean, or double.

Block Characteristics

Data Types	Boolean | double | fixed pointa | integer | single
Multidimensional Signals	no
Variable-Size Signals	no
a ufix(1) only.

More About

Input and Output Signal Length in RS Blocks

The Reed-Solomon code has a message word length, K, or shortened message word length, S. The codeword length is N – K + S – P, where N is the full codeword length and P is the number of punctures per codeword. When there is no message shortening, the codeword length expression reduces to N – P, because K = S. If the decoder is processing multiple codewords per frame, then the same puncture pattern holds for all codewords.

This table provides expressions for the input and output signal lengths for the Reed-Solomon encoder and decoder.

The notation y = N_C × x denotes that y is an integer multiple of x.

	Input, Erasure, and Output Vector Lengths
RS Block Coder	No Message Shortening Used	Message Shortening Used
Binary-Input RS Encoder	Input Length (bits): NC × K × M Output Length (bits): NC × (N–P) × M	Input Length (bits): NC × S × M Output Length (bits): NC × (N–K+S–P) × M
Binary-Output RS Decoder	Input Length (bits): NC × (N–P) × M Erasures Length (symbols): NC × (N–P) Output Length (bits): NC × K × M	Input Length (bits): NC × (N–K+S–P) × M Erasures Length (symbols): NC × (N–K+S–P) Output Length (bits): NC × S × M

• N is the codeword length.

• K is the message word length.

• S is the shortened message word length.

• N_C is the number of codewords (and message words).

• P is the number of punctures per codeword, and is equal to the number of zeros in the puncture vector.

• M is the degree of the primitive polynomial. Each group of M bits represents an integer between 0 and 2M–1 that belongs to the finite Galois field GF(2M).

For more information on representing data for Reed-Solomon codes, see Integer Format (Reed-Solomon Only).

Also, see Restrictions on the M and the Codeword Length N.

Restrictions on the M and the Codeword Length N

• If you do not select Specify primitive polynomial, valid values for the codeword length, N, are from 7 to 65535. In this case, the block uses the default primitive polynomial of degree M = ceil(log2(N+1)). You can display the default primitive polynomial by running primpoly(ceil(log2(N+1))).

• If you select Specify primitive polynomial, valid values for the primitive polynomial degree, M, are from 3 to 16. The valid values for N in this case are from 7 to 2^M–1. Selecting Specify primitive polynomial enables you to specify the primitive polynomial that defines the finite field GF(2^M), which corresponds to the values that form message words and codewords.

Specify the Generator Polynomial

Select Specify generator polynomial to enable the Generator polynomial parameter for specifying the generator polynomial of the Reed-Solomon code. Enter an integer row vector with element values from 0 to 2^M-1. The vector represents a polynomial, in descending order of powers, whose coefficients are elements of GF(2^M) represented in integer format. For more information about integer and binary format, see Integer Format (Reed-Solomon Only). The generator polynomial must be equal to a polynomial with this factored form:

g(x) = (x+α^b)(x+α^b+1)(x+α^b+2)...(x+α^b+N-K-1)

α is the primitive element of the Galois field over which the input message is defined, and b is an integer.

If you do not select Specify generator polynomial, the block uses the default generator polynomial, corresponding to b=1, for Reed-Solomon encoding. You can display the default generator polynomial by running rsgenpoly.

• If you are using the default primitive polynomial (Specify primitive polynomial is not selected), the default generator polynomial is rsgenpoly(N,K), where N = 2M-1.

• If you are not using the default primitive polynomial (Specify primitive polynomial is selected) and you specify the primitive polynomial as poly, the generator polynomial is rsgenpoly(N,K,poly).

Note

The degree of the generator polynomial is N − K, where N is the codeword length and K is the message word length.

Puncturing and Erasures

1s and 0s have precisely opposite meanings for the puncture and erasure vectors.

In a puncture vector,

• 1 means that the data symbol is passed through the block unaltered.

• 0 means that the data symbol is to be punctured, or removed, from the data stream.

In an erasure vector,

• 1 means that the data symbol is to be replaced with an erasure symbol.

• 0 means that the data symbol is passed through the block unaltered.

These conventions apply to both the encoder and the decoder. For more information, see Shortening, Puncturing, and Erasures.

Supported Data Types

Port	Supported Data Types
In	Double-precision floating point Single-precision floating point Boolean 8-, 16-, and 32-bit signed integers 8-, 16-, and 32-bit unsigned integers 1-bit unsigned integer (ufix(1))
Out

Algorithms

This object implements the algorithm, inputs, and outputs described in Algorithms for BCH and RS Errors-only Decoding.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced before R2006a