SI Controller

Spark-ignition engine controller that uses the driver torque request

• 

×

Libraries:
Powertrain Blockset / Propulsion / Combustion Engine Controllers

Description

The SI Controller block implements a spark-ignition (SI) controller that uses the driver torque request to calculate the open-loop air, fuel, and spark actuator commands that are required to meet the driver demand.

You can use the SI Controller block in engine control design or performance, fuel economy, and emission tradeoff studies. The core engine, throttle, and turbocharger wastegate subsystems require the commands that are output from the SI Controller block.

The block uses the commanded torque and engine speed to determine these open-loop actuator commands:

• Throttle position percent

• Wastegate area percent

• Injector pulse-width

• Spark advance

• Intake cam phaser angle

• Exhaust cam phaser angle

• Exhaust gas recirculation (EGR) valve area percent

The SI Controller block has two subsystems:

• The Controller subsystem — Determines the commands based on the commanded torque, measured engine speed, and estimated cylinder air mass.

• The Estimator subsystem — Determines the estimated air mass flow, torque, and exhaust gas temperature from intake manifold gas pressure, intake manifold gas temperature, engine speed, and cam phaser positions.

The figure illustrates the signal flow.

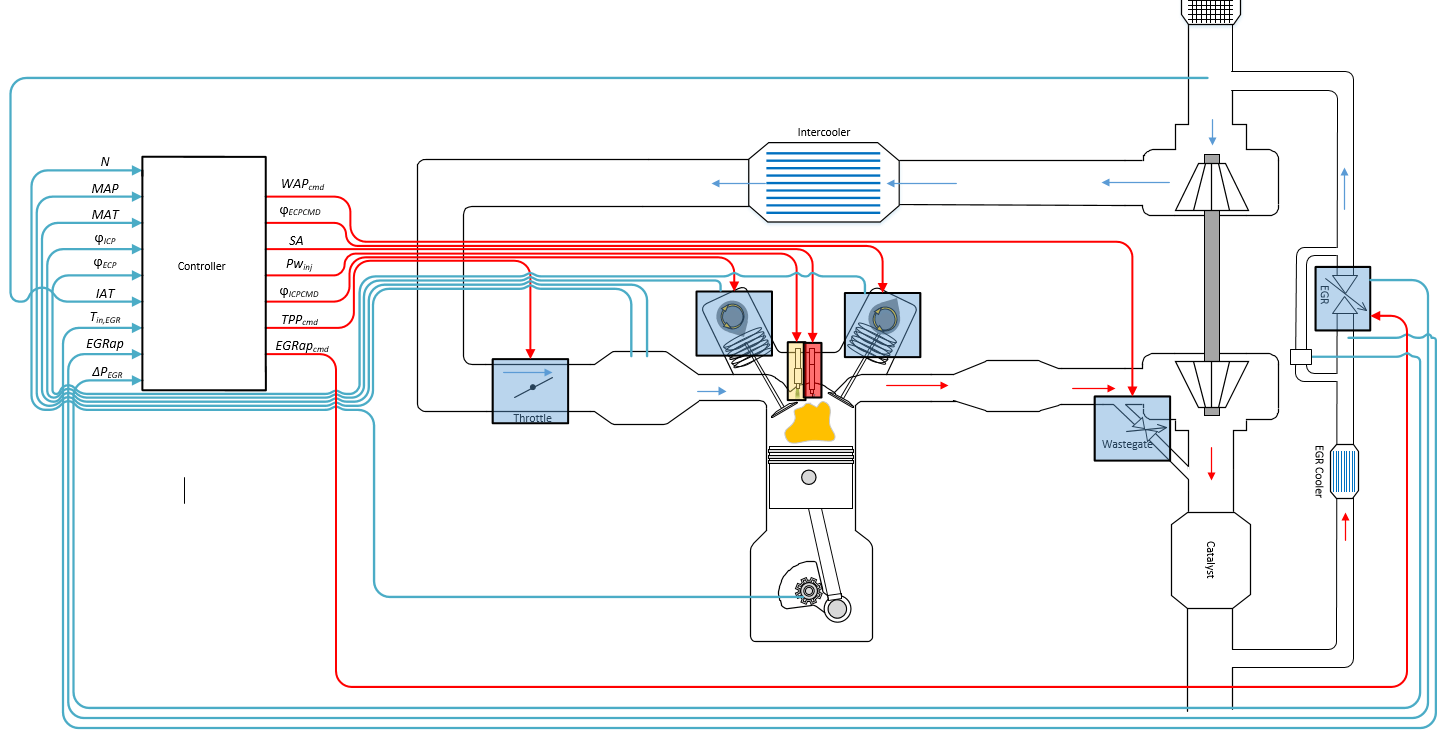
The figure uses these variables.

N	Engine speed
MAP	Cycle average intake manifold pressure
IAT	Intake air temperature
Tin,EGR	Temperature at EGR valve inlet
MAT	Cycle average intake manifold gas absolute temperature
${\phi }_{ICP}$, ${\phi }_{ICPCMD}$	Intake cam phaser angle and intake cam phaser angle command, respectively
${\phi }_{ECP}$, ${\phi }_{ECPCMD}$	Exhaust cam phaser angle and exhaust cam phaser angle command, respectively
EGRap, EGRapcmd	EGR valve area percent and EGR valve area percent command, respectively
ΔPEGR	Pressure difference at EGR valve inlet and outlet
WAPcmd	Turbocharger wastegate area percent command
SA	Spark advance
$P{w}_{inj}$	Fuel injector pulse-width
TPPcmd	Throttle position percent command

The Model-Based Calibration Toolbox™ was used to develop the tables that are available with the Powertrain Blockset™.

Controller

Air

The block determines the commanded engine load (that is, normalized cylinder air mass) from a lookup table that is a function of commanded torque and measured engine speed.

$L_{cmd}=f_{Lcmd}\left(T_{cmd},N\right)$

To achieve the commanded load, the controller sets the throttle position percent and turbocharger wastegate area percent using feed forward lookup tables. The lookup tables are functions of the commanded load and measured engine speed.

$TA{P}_{cmd}=f_{TAPcmd}\left(L_{cmd},N\right)$

$TP{P}_{cmd}=f_{TPPcmd}\left(TA{P}_{cmd}\right)$

$WA{P}_{cmd}=f_{WAPcmd}\left(L_{cmd},N\right)$

To determine the cam phaser angle commands, the block uses lookup tables that are functions of estimated engine load and measured engine speed.

${\phi }_{ICPCMD}=f_{ICPCMD}\left(L_{est},N\right)$

${\phi }_{ECPCMD}=f_{ECPCMD}\left(L_{est},N\right)$

The block calculates the desired engine load using this equation.

$$L_{est}=\frac{Cps{R}_{air}{T}_{std}{\dot{m}}_{air,est}}{P_{std}{V}_{d}N}$$

The equations use these variables.

Lest	Estimated engine load
Lcmd	Commanded engine load
N	Engine speed
Tcmd	Commanded engine torque
TAPcmd	Throttle area percent command
TPPcmd	Throttle position percent command
WAPcmd	Turbocharger wastegate area percent command
$$Cps$$	Crankshaft revolutions per power stroke
$P_{std}$	Standard pressure
$T_{std}$	Standard temperature
$R_{air}$	Ideal gas constant for air and burned gas mixture
$V_d$	Displaced volume
${\dot{m}}_{air,est}$	Estimated engine air mass flow

The controller subsystem uses these lookup tables for the air calculations.

• The throttle area percent command lookup table, $f_{TAPcmd}$, is a function of commanded load and engine speed

  $TA{P}_{cmd}=f_{TAPcmd}\left(L_{cmd},N\right)$

  where:

  • TAP_cmd is throttle area percentage command, in percent.

  • L_cmd=L is commanded engine load, dimensionless.

  • N is engine speed, in rpm.

  

• To account for the non-linearity of the throttle position to throttle area, the throttle position percent lookup table linearizes the open-loop air mass flow control.

  The throttle position percent command lookup table, $f_{TPPcmd}$, is a function of the throttle area percentage command

  $TP{P}_{cmd}=f_{TPPcmd}\left(TA{P}_{cmd}\right)$

  where:

  • TPP_cmd is throttle position percentage command, in percent.

  • TAP_cmd is throttle area percentage command, in percent.

  

• The wastegate area percent command lookup table, $f_{WAPcmd}$, is a function of the commanded engine load and engine speed

  $WA{P}_{cmd}=f_{WAPcmd}\left(L_{cmd},N\right)$

  where:

  • WAP_cmd is wastegate area percentage command, in percent.

  • L_cmd=L is commanded engine load, dimensionless.

  • N is engine speed, in rpm.

  

• The commanded engine load lookup table, $f_{Lcmd}$, is a function of the commanded torque and engine speed

  $L_{cmd}=f_{Lcmd}\left(T_{cmd},N\right)$

  where:

  • L_cmd=L is commanded engine load, dimensionless.

  • T_cmd is commanded torque, in N·m.

  • N is engine speed, in rpm.

  

• The intake cam phaser angle command lookup table, $f_{ICPCMD}$, is a function of the engine load and engine speed

  ${\phi }_{ICPCMD}=f_{ICPCMD}\left(L_{est},N\right)$

  where:

  • ${\phi }_{ICPCMD}$ is commanded intake cam phaser angle, in crank degrees advance from park.

  • L_est=L is estimated engine load, dimensionless.

  • N is engine speed, in rpm.

  

• The exhaust cam phaser angle command lookup table, $f_{ECPCMD}$, is a function of the engine load and engine speed

  ${\phi }_{ECPCMD}=f_{ECPCMD}\left(L_{est},N\right)$

  where:

  • ${\phi }_{ECPCMD}$ is commanded exhaust cam phaser angle, in crank degrees retard from park.

  • L_est=L is estimated engine load, dimensionless.

  • N is engine speed, in rpm.

  

EGR

EGR is typically expressed as a percent of total intake port flow.

$$EG{R}_{pct}=100\frac{{\dot{m}}_{EGR}}{{\dot{m}}_{EGR}+{\dot{m}}_{air}}$$

To calculate the EGR area percent command, the block uses equations and a lookup table.

Equations

$$\begin{array}{l}{\dot{m}}_{EGRstd,cmd}={\dot{m}}_{EGR,cmd}\frac{P_{std}}{P_{in,EGR}}\sqrt{\frac{T_{in,EGR}}{T_{std}}}\\ \\ {\dot{m}}_{EGRstd,max}=f_{EGRstd,max}\left(\frac{P_{out,EGR}}{P_{in,EGR}}\right)\\ \\ {\dot{m}}_{EGR,cmd}=EG{R}_{pct,cmd}{\dot{m}}_{intk,est}\end{array}$$

Lookup table

The EGR area percent command, EGRapcmd, lookup table is a function of the normalized mass flow and pressure ratio $$EGRa{p}_{cmd}=f_{EGRap,cmd}\left(\frac{{\dot{m}}_{EGRstd,cmd}}{{\dot{m}}_{EGRstd,max}},\frac{P_{out,EGR}}{P_{in,EGR}}\right)$$ where: EGRapcmd is commanded EGR area percent, dimensionless. $$\frac{{\dot{m}}_{EGRstd,cmd}}{{\dot{m}}_{EGRstd,max}}$$ is the normalized mass flow, dimensionless. $$\frac{P_{out,EGR}}{P_{in,EGR}}$$ is the pressure ratio, dimensionless.

The equations and table use these variables.

EGRap, EGRapcmd	EGR valve area percent and EGR valve area percent command, respectively
EGRpct,cmd	EGR percent command
$${\dot{m}}_{EGRstd,cmd}$$	Commanded standard mass flow
$${\dot{m}}_{EGRstd,max}$$	Maximum standard mass flow
$${\dot{m}}_{EGR,cmd}$$	Commanded mass flow
$${\dot{m}}_{intk,est}$$	Estimated intake port mass flow
Tstd, Pstd	Standard temperature and pressure
Tin,EGR	Temperature at EGR valve inlet
Pout,EGR, Pin,EGR	Pressure at EGR valve inlet and outlet, respectively

Fuel

The air-fuel ratio (AFR) impacts three-way-catalyst (TWC) conversion efficiency, torque production, and combustion temperature. The engine controller manages AFR by commanding injector pulse-width from a desired relative AFR. The relative AFR, $${\lambda }_{cmd}$$, is the ratio between the commanded AFR and the stoichiometric AFR of the fuel.

${\lambda }_{cmd}=\frac{AF{R}_{cmd}}{AF{R}_{stoich}}$

$$AF{R}_{cmd}=\frac{{\dot{m}}_{air,est}}{{\dot{m}}_{fuel,cmd}}$$

The SI Controller block accounts for the extra fuel delivered to the SI engine during startup. If the engine speed is greater than the startup engine cranking speed, the SI Controller block enriches the optimal AFR, lambda, with an exponentially decaying delta lambda. To initialize the delta lambda, the block uses the engine coolant temperature at startup. The delta lambda exponentially decays to zero based on a time constant that is a function of the engine coolant temperature.

You can configure the block for open-loop and closed-loop AFR control.

To	Use	Controls > Fuel > Closed-loop feedback Parameter Setting
Assess the dynamic and steady-state accuracy of the controller airflow estimation and fuel delivery.	(default) Open-loop control	off
Hold the average AFR close to stoichiometric AFR to maintain a high TWC conversion efficiency.	Closed-loop control	on

Open-Loop Control

To create an input port for the commanded AFR (lambda), on the Controls > Fuel > Open-loop fuel pane, select Input lambda.

You can manually tune the catalyst for maximum efficiency during open-loop AFR control with or without dither. If you want to implement dither during open-loop control, on the Fuel tab, on the Closed-loop fuel pane, select Dither.

By default, the block is configured to use a lookup table for the commanded AFR.

The commanded lambda, $${\lambda }_{cmd}$$, lookup table is a function of estimated engine load and measured engine speed

${\lambda }_{cmd}=f_{\lambda cmd}\left(L_{est},N\right)$

where:

• $${\lambda }_{cmd}$$ is commanded relative AFR, dimensionless.

• L_est=L is estimated engine load, dimensionless.

• N is engine speed, in rpm.

The block calculates the estimated fuel mass flow rate using the commanded lambda, $${\lambda }_{cmd}$$, stoichiometric AFR, and estimated air mass flow rate.

$${\dot{m}}_{fuel,cmd}=\frac{{\dot{m}}_{air,est}}{AF{R}_{cmd}}=\frac{{\dot{m}}_{air,est}}{{\lambda }_{cmd}AF{R}_{stoich}}$$

The block assumes that the battery voltage and fuel pressure are at nominal settings where pulse-width correction is not necessary. The commanded fuel injector pulse-width is proportional to the fuel mass per injection. The fuel mass per injection is calculated from the commanded fuel mass flow rate, engine speed, and the number of cylinders.

$P{w}_{inj}=\{\begin{array}{cc}\frac{{\dot{m}}_{fuel,cmd}Cps(\frac{60s}{min})\left(\frac{1000mg}{g}\right)\left(\frac{1000g}{kg}\right)}{N{S}_{inj}{N}_{cyl}}& \text{when }Tr{q}_{cmd}>0\\ 0& \text{when }Tr{q}_{cmd}\le 0\end{array}$

Closed-Loop Control

TWC converters are most efficient when the exhaust AFR is near the stoichiometric AFR, where the air and fuel burn most completely. Around this ideal point, the AFR is within the catalyst window in which the catalyst is most efficient at converting carbon monoxide, hydrocarbons, and nitrogen oxides to non-harmful exhaust products. Empirical studies show that oscillating the AFR around stoichiometry at an optimized AFR frequency, amplitude, and bias widens the TWC window, increasing catalyst conversion efficiency in the presence of unavoidable disturbances.

To keep production hardware costs down, AFR control systems include inexpensive switching oxygen sensors positioned in the engine exhaust stream upstream and downstream of the catalyst. The oxygen sensors have a narrow range. Essentially, they switch between too lean (i.e., more air is available than is required to burn the available fuel) and too rich (i.e., more air is available than is required to burn the available fuel).

The block implements a period-based method to control the average AFR at a value within the catalyst window for maximum conversion efficiency. Period-based AFR control is independent of the transport delay across the engine from the fuel injection point to the sensor measurement point. For more information about the method, see Developing a Period-Based Air-Fuel Ratio Controller Using a Low-Cost Switching Sensor.

Spark

Spark advance is the crank angle before top dead center (BTDC) of the power stroke when the spark is delivered. The spark advance has an impact on engine efficiency, torque, exhaust temperature, knock, and emissions.

The spark advance lookup table is a function of estimated load and engine speed.

$SA=f_{SA}\left(L_{est},N\right)$

where:

• SA is spark advance, in crank advance degrees.

• L_est=L is estimated engine load, dimensionless.

• N is engine speed, in rpm.

The equations use these variables.

Lest	Estimated engine load, based on normalized cylinder air mass
N	Engine speed
$f_{SA}$	Lookup table for spark advance
N	Spark advance

Idle Speed

When the commanded torque is below a threshold value, the idle speed controller regulates the engine speed.

If	Idle Speed Controller
Trqcmd,input < Trqidlecmd,enable	Enabled
Trqidlecmd,enable ≤ Trqcmd,input	Not enabled

The idle speed controller uses a discrete PI controller to regulate the target idle speed by commanding a torque.

The PI controller uses this transfer function:

$C_{idle}\left(z\right)=K_{p,idle}+K_{i,idle}\frac{t_s}{z-1}$

The idle speed commanded torque must be less than the maximum commanded torque:

0 ≤ Trq_idlecomd ≤Trq_idlecmd,max

Idle speed control is active under these conditions. If the commanded input torque drops below the threshold for enabling the idle speed controller (Trq_cmd,input < Trq_{idlecmd,enable}), the commanded engine torque is given by:

Trq_cmd = max(Trq_cmd,input,Trq_idlecmd).

The equations use these variables.

Trqcmd	Commanded engine torque
Trqcmd,input	Input commanded engine torque
Trqidlecmd,enable	Threshold for enabling idle speed controller
Trqidlecmd	Idle speed controller commanded torque
Trqidlecmd,max	Maximum commanded torque
Nidle	Base idle speed
Kp,idle	Idle speed controller proportional gain
Ki,idle	Idle speed controller integral gain

Speed Limiter

To prevent over revving the engine, the block implements an engine speed limit controller that limits the engine speed to the value specified by the Rev-limiter speed threshold parameter on the Controls > Idle Speed tab.

If the engine speed, N, exceeds the engine speed limit, N_lim, the block sets the commanded engine torque to 0.

To smoothly transition the torque command to 0 as the engine speed approaches the speed limit, the block implements a lookup table multiplier. The lookup table multiplies the torque command by a value that ranges from 0 (engine speed exceeds limit) to 1 (engine speed does not exceed the limit).

Estimator

The estimator subsystem determines the estimated air mass flow, torque, EGR mass flow, and exhaust temperature based on sensor feedback and calibration parameters.

${\dot{m}}_{air,est}$	Estimated engine air mass flow
Trqest	Estimated engine torque
Texh,est	Estimated engine exhaust temperature
$${\dot{m}}_{EGR,est}$$	Estimated low-pressure EGR mass flow

Air Mass Flow

To calculate engine air mass flow, configure the SI engine to use either of these air mass flow models.

Air Mass Flow Model	Description
SI Engine Speed-Density Air Mass Flow Model	Uses the speed-density equation to calculate the engine air mass flow, relating the engine air mass flow to the intake manifold pressure and engine speed. Consider using this air mass flow model in engines with fixed valvetrain designs.
SI Engine Dual-Independent Cam Phaser Air Mass Flow Model	To calculate the engine air mass flow, the dual-independent cam phaser model uses: Empirical calibration parameters developed from engine mapping measurements Desktop calibration parameters derived from engine computer-aided design (CAD) data In contrast to typical embedded air mass flow calculations based on direct air mass flow measurement with an air mass flow (MAF) sensor, this air mass flow model offers: Elimination of MAF sensors in dual cam-phased valvetrain applications Reasonable accuracy with changes in altitude Semiphysical modeling approach Bounded behavior Suitable execution time for electronic control unit (ECU) implementation Systematic development of a relatively small number of calibration parameters

To determine the estimated air mass flow, the block uses the intake air mass fraction. The EGR mass fraction at the intake port lags the mass fraction near the EGR valve outlet. To model the lag, the block uses a first order system with a time constant.

$$y_{intk,EGR,est}=\frac{{\dot{m}}_{EGR,est}}{{\dot{m}}_{intk,est}}\frac{t_{s}z}{{\tau }_{EGR}z+t_s-{\tau }_{EGR}}$$

The remainder of the gas is air.

$$y_{intk,air,est}=1-y_{intk,EGR,est}$$

The equations use these variables.

yintk,EGR,est	Estimated intake manifold EGR mass fraction
yintk,air,est	Estimated intake manifold air mass fraction
$${\dot{m}}_{EGR,est}$$	Estimated low-pressure EGR mass flow
$${\dot{m}}_{intk,est}$$	Estimated intake port mass flow
τEGR	EGR time constant

Torque

To calculate the brake torque, configure the SI engine to use either of these torque models.

Brake Torque Model	Description
SI Engine Torque Structure Model	For the structured brake torque calculation, the SI engine uses tables for the inner torque, friction torque, optimal spark, spark efficiency, and lambda efficiency. If you select Crank angle pressure and torque on the block Torque tab, you can: Simulate advanced closed-loop engine controls in desktop simulations and on HIL bench, based on cylinder pressure recorded from a model or laboratory test as a function of crank angle. Simulate driveline vibrations downstream of the engine due to high-frequency crankshaft torsionals. Simulate engine misfires due to lean operation or spark plug fouling by using the injector pulse width input. Simulate cylinder deactivation effect (closed intake and exhaust valves, no injected fuel) on individual cylinder pressures, mean-value airflow, mean-value torque, and crank-angle-based torque. Simulate the fuel-cut effect on individual cylinder pressure, mean-value torque, and crank-angle-based torque.
SI Engine Simple Torque Model	For the simple brake torque calculation, the SI engine block uses a torque lookup table map that is a function of engine speed and load.

EGR

The controller estimates low-pressure mass flow, EGR valve inlet pressure, and EGR valve outlet pressure using an algorithm developed by F. Liu and J. Pfeiffer. The estimator requires measured EGR valve differential pressure, EGR valve area percent, intake air temperature, and EGR valve inlet temperature.

To estimate the EGR valve commands, the block uses:

• Equations

  $$\begin{array}{l}{\dot{m}}_{air,std}={\dot{m}}_{air,est}\frac{P_{std}}{P_{amb}}\sqrt{\frac{IAT}{T_{std}}}\\ \\ P_{in,EGR}=P_{out,EGR}+\Delta P_{EGR}\\ \\ {\dot{m}}_{EGR,est}={\dot{m}}_{EGR,std}\frac{P_{in,EGR}}{P_{std}}\sqrt{\frac{T_{std}}{T_{in,EGR}}}\end{array}$$

• Tables

  • The EGR valve standard mass flow lookup table is a function of EGR valve area percent and the pressure ratio

    $${\dot{m}}_{EGR,std}=f_{EGR,std}\left(EGRap,\frac{P_{out,EGR}}{P_{in,EGR}}\right)$$

    where:

    • $${\dot{m}}_{EGR,std}$$ is EGR valve standard mass flow, dimensionless.

    • EGRap is EGR valve flow area percent, in percent.

    • $$\frac{P_{out,EGR}}{P_{in,EGR}}$$ is the pressure ratio, dimensionless.

    

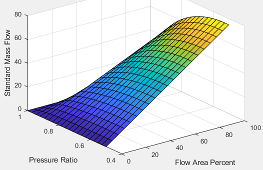
  • The pressure ratio is a function of the standard mass flow

    $$\frac{P_{out,EGR}}{P_{amb}}=f_{intksys,pr}({\dot{m}}_{air,std})$$

    where:

    • $${\dot{m}}_{air,std}$$ is standard mass flow, in g/s.

    • $$\frac{P_{out,EGR}}{P_{amb}}$$ is pressure ratio, dimensionless.

    

The equations use these variables.

EGRap	EGR valve area percent command
IAT	Intake air temperature
$${\dot{m}}_{air,std}$$, $${\dot{m}}_{EGR,std}$$	Standard air and EGR valve mass flow, respectively
${\dot{m}}_{air,est}$,$${\dot{m}}_{EGR,est}$$	Estimated air and EGR valve mass flow, respectively
Tstd, Pstd	Standard temperature and pressure
Tamb, Pamb	Ambient temperature and pressure
ΔPEGR	Pressure difference at EGR valve inlet and outlet
Tin,EGR, Tout,EGR	Temperature at EGR valve inlet and outlet, respectively
Pin,EGR, Pout,EGR	Pressure at EGR valve inlet and outlet, respectively

Exhaust Temperature

The exhaust temperature lookup table, $f_{Texh}$, is a function of engine load and engine speed

$T_{exh}=f_{Texh}(L,N)$

where:

• T_exh is engine exhaust temperature, in K.

• L is normalized cylinder air mass or engine load, dimensionless.

• N is engine speed, in rpm.

Examples

Build Conventional Vehicle Model

Build a vehicle with an internal combustion engine using the conventional vehicle reference application.

Calibrate, Validate, and Optimize SI Engine with Dynamometer Test Harness

Simulate a spark-ignition (SI) engine and controller under a dynamometer test harness using the SI engine dynamometer reference application.

Ports

Input

TrqCmd — Commanded engine torque

scalar

Commanded engine torque, Trq_cmd,input, in N·m.

EngSpd — Measured engine speed

scalar

Measured engine speed, N, in rpm.

AmbPrs — Measured absolute ambient pressure

scalar

Measured ambient pressure, $P_{Amb}$, in Pa.

Map — Measured intake manifold absolute pressure

scalar

Measured intake manifold absolute pressure$MAP$, in Pa.

Mat — Measured intake manifold absolute temperature

scalar

Measured intake manifold absolute temperature, $MAT$, in K.

IntkCamPhase — Intake cam phaser angle

scalar

Intake cam phaser angle, ${\phi }_{ICP}$, in degCrkAdv, or crank degrees advance from park.

ExhCamPhase — Exhaust cam phaser angle

scalar

Exhaust cam phaser angle, ${\phi }_{ECP}$, in degCrkRet, or crank degrees retard from park.

Iat — Intake air temperature

scalar

Intake air temperature, IAT, in K.

Ect — Engine cooling temperature

scalar

Engine cooling temperature, T_coolant, in K.

EgrVlvInTemp — EGR valve inlet temperature

scalar

EGR valve inlet temperature, T_in,EGR, in K.

EgrVlvAreaPct — EGR valve area percent

scalar

EGR valve area percent, EGRap, in %.

EgrVlvDeltaPrs — EGR valve delta pressure

scalar

EGR valve delta pressure, ΔP_EGR, in Pa.

O2VoltSen — Oxygen sensor voltage

scalar

Oxygen sensor voltage for closed-loop air-fuel-ratio (lambda) control, in mV.

To configure the block to use closed-loop air-fuel-ratio control, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

LambdaCmd — Commanded AFR, lambda

scalar

Commanded air-fuel-ratio (lambda), λ_cmd, dimensionless.

Dependencies

To create this port, on the Fuel tab, on the Open-loop fuel pane, select Input lambda.

IgSw — Ignition switch

Boolean

State of the vehicle ignition switch, dimensionless.

Dependencies

To create this port, on the Stop-Start tab, select Enable Engine Stop-Start.

ESSEnable — Engine Stop-Start Enable

Boolean

Command to enable or disable the stop-start logic, dimensionless.

Dependencies

To create this port, on the Stop-Start tab, select Enable Engine Stop-Start. Select External Enable Port.

Output

Info — Bus signal

bus

Bus signal containing these block calculations.

Signal	Description	Variable	Units
TrqCmd	Engine torque	Trqcmd	N·m
LdCmd	Commanded load	Lcmd	N/A
ThrPosCmd	Throttle area percent command	TAPcmd	%
WgAreaPctCmd	Wastegate area percent command	WAPcmd	%
InjPw	Fuel injector pulse-width	$P{w}_{inj}$	ms
SpkAdv	Spark advance	$SA$	degBTDC
IntkCamPhaseCmd	Intake cam phaser angle command	${\phi }_{ICPCMD}$	degCrkAdv
ExhCamPhaseCmd	Exhaust cam phaser angle command	${\phi }_{ECPCMD}$	degCrkRet
EgrVlvAreaPctCmd	Exhaust cam phaser angle command	EGRapcmd	%
FuelMassFlwCmd	EGR valve area percent command	${\dot{m}}_{fuel,cmd}$	kg/s
AfrCmd	Commanded air-fuel ratio	AFRcmd	N/A
EstEngTrq	Estimated engine torque	Trqest	N·m
EstNrmlzdAirCharg	Estimated normalized cylinder air mass	N/A	N/A
EstIntkPortMassFlw	Estimated intake port air mass flow rate	$${\dot{m}}_{intk,est}$$	kg/s
EstIntkAirMassFlw	Estimated air mass flow rate	${\dot{m}}_{air,est}$	kg/s
EstEgrMassFlw	Estimated low-pressure EGR mass flow rate	$${\dot{m}}_{EGR,est}$$	kg/s
EstExhManGasTemp	Estimated exhaust manifold gas temperature	Texh,est	K
EngRevLimAct	Flag that indicates if rev-limiter control is active	N/A	N/A
ClsdLpFuelMult	Fuel injector pulse-width multiplier for closed-loop AFR control	Pwinj_mult	N/A

ThrPosPctCmd — Throttle area percent command

scalar

Throttle area percent command, TAP_cmd.

WgAreaPctCmd — Wastegate area percent command

scalar

Wastegate area percent command, WAP_cmd.

InjPw — Fuel injector pulse-width

scalar

Fuel injector pulse-width, $P{w}_{inj}$, in ms.

SpkAdv — Spark advance

scalar

Spark advance, $SA$, in degrees crank angle before top dead center (degBTDC).

IntkCamPhaseCmd — Intake cam phaser angle command

scalar

Intake cam phaser angle command, ${\phi }_{ICPCMD}$.

ExhCamPhaseCmd — Exhaust cam phaser angle command

scalar

Exhaust cam phaser angle command, ${\phi }_{ECPCMD}$.

EgrVlvAreaPctCmd — EGR valve area percent command

scalar

EGR valve area percent command, EGRap_cmd, in %.

Parameters

Configuration

Air mass flow estimation model — Select air mass flow estimation model

Dual Variable Cam Phasing (default) | Simple Speed-Density

To calculate engine air mass flow, configure the SI engine to use either of these air mass flow models.

Air Mass Flow Model	Description
SI Engine Speed-Density Air Mass Flow Model	Uses the speed-density equation to calculate the engine air mass flow, relating the engine air mass flow to the intake manifold pressure and engine speed. Consider using this air mass flow model in engines with fixed valvetrain designs.
SI Engine Dual-Independent Cam Phaser Air Mass Flow Model	To calculate the engine air mass flow, the dual-independent cam phaser model uses: Empirical calibration parameters developed from engine mapping measurements Desktop calibration parameters derived from engine computer-aided design (CAD) data In contrast to typical embedded air mass flow calculations based on direct air mass flow measurement with an air mass flow (MAF) sensor, this air mass flow model offers: Elimination of MAF sensors in dual cam-phased valvetrain applications Reasonable accuracy with changes in altitude Semiphysical modeling approach Bounded behavior Suitable execution time for electronic control unit (ECU) implementation Systematic development of a relatively small number of calibration parameters

Dependencies

The table summarizes the parameter dependencies.

Air Mass Flow Estimation Model	Enables Parameters on Estimation > Air Tab
Dual Variable Cam Phasing	Cylinder volume at intake valve close table, f_vivc Cylinder volume intake cam phase breakpoints, f_vivc_icp_bpt Cylinder trapped mass correction factor, f_tm_corr Normalized density breakpoints, f_tm_corr_nd_bpt Engine speed breakpoints, f_tm_corr_n_bpt Air mass flow, f_mdot_air Exhaust cam phase breakpoints, f_mdot_air_ecp_bpt Trapped mass flow breakpoints, f_mdot_trpd_bpt Air mass flow correction factor, f_mdot_air_corr Engine load breakpoints for air mass flow correction, f_mdot_air_corr_ld_bpt Engine speed breakpoints for air mass flow correction, f_mdot_air_n_bpt
Simple Speed-Density	Speed-density volumetric efficiency, f_nv Speed-density intake manifold pressure breakpoints, f_nv_prs_bpt Speed-density engine speed breakpoints, f_nv_n_bpt

Torque estimation model — Select torque estimation model

Torque Structure (default) | Simple Torque Lookup

To calculate the brake torque, configure the SI engine to use either of these torque models.

Brake Torque Model	Description
SI Engine Torque Structure Model	For the structured brake torque calculation, the SI engine uses tables for the inner torque, friction torque, optimal spark, spark efficiency, and lambda efficiency. If you select Crank angle pressure and torque on the block Torque tab, you can: Simulate advanced closed-loop engine controls in desktop simulations and on HIL bench, based on cylinder pressure recorded from a model or laboratory test as a function of crank angle. Simulate driveline vibrations downstream of the engine due to high-frequency crankshaft torsionals. Simulate engine misfires due to lean operation or spark plug fouling by using the injector pulse width input. Simulate cylinder deactivation effect (closed intake and exhaust valves, no injected fuel) on individual cylinder pressures, mean-value airflow, mean-value torque, and crank-angle-based torque. Simulate the fuel-cut effect on individual cylinder pressure, mean-value torque, and crank-angle-based torque.
SI Engine Simple Torque Model	For the simple brake torque calculation, the SI engine block uses a torque lookup table map that is a function of engine speed and load.

Dependencies

The table summarizes the parameter dependencies.

Torque Estimation Model	Enables Parameters on Estimation > Torque Tab
Torque Structure	Inner torque table, f_tq_inr Friction torque table, f_tq_fric Engine temperature modifier on friction torque, f_fric_temp_mod Engine temperature modifier breakpoints, f_fric_temp_bpt Pumping torque table, f_tq_pump Optimal spark table, f_sa_opt Inner torque load breakpoints, f_tq_inr_l_bpt Inner torque speed breakpoints, f_tq_inr_n_bpt Spark efficiency table, f_m_sa Spark retard from optimal, f_del_sa_bpt Lambda efficiency, f_m_lam Lambda breakpoints, f_m_lam_bpt
Simple Torque Lookup	Torque table, f_tq_nl Torque table load breakpoints, f_tq_nl_l_bpt Torque table speed breakpoints, f_tq_nl_n_bpt

Controls

Air

Engine commanded load table, f_lcmd — Lookup table

array

The commanded engine load lookup table, $f_{Lcmd}$, is a function of the commanded torque and engine speed

$L_{cmd}=f_{Lcmd}\left(T_{cmd},N\right)$

where:

• L_cmd=L is commanded engine load, dimensionless.

• T_cmd is commanded torque, in N·m.

• N is engine speed, in rpm.

Torque command breakpoints, f_lcmd_tq_bpt — Breakpoints

[15 26.43 37.86 49.29 60.71 72.14 83.57 95 106.4 117.9 129.3 140.7 152.1 163.6 175] (default) | vector

Torque command breakpoints, in N·m.

Speed breakpoints, f_lcmd_n_bpt — Breakpoints

[750 1054 1357 1661 1964 2268 2571 2875 3179 3482 3786 4089 4393 4696 5000] (default) | vector

Speed breakpoints, in rpm.

Throttle area percent, f_tap — Lookup table, %

array

The throttle area percent command lookup table, $f_{TAPcmd}$, is a function of commanded load and engine speed

$TA{P}_{cmd}=f_{TAPcmd}\left(L_{cmd},N\right)$

where:

• TAP_cmd is throttle area percentage command, in percent.

• L_cmd=L is commanded engine load, dimensionless.

• N is engine speed, in rpm.

Throttle area percent load breakpoints, f_tap_ld_bpt — Breakpoints

[0.2 0.275 0.35 0.425 0.5 0.575 0.65 0.725 0.8 0.875 0.95 1.025 1.1 1.175 1.25] (default) | vector

Throttle area percent load breakpoints, dimensionless.

Throttle area percent speed breakpoints, f_tap_n_bpt — Breakpoints

[750 1054 1357 1661 1964 2268 2571 2875 3179 3482 3786 4089 4393 4696 5000] (default) | vector

Throttle area percent speed breakpoints, in rpm.

Throttle area percent to position percent table, f_tpp — Lookup table

[0 100] (default) | vector

The throttle position percent command lookup table, $f_{TPPcmd}$, is a function of the throttle area percentage command

$TP{P}_{cmd}=f_{TPPcmd}\left(TA{P}_{cmd}\right)$

where:

• TPP_cmd is throttle position percentage command, in percent.

• TAP_cmd is throttle area percentage command, in percent.

Throttle area percent to position percent area breakpoints, f_tpp_tap_bpt — Breakpoints

[0 100] (default) | vector

Throttle area percent to position percent area breakpoints, dimensionless.

Wastegate area percent, f_wap — Lookup table, %

array

The wastegate area percent command lookup table, $f_{WAPcmd}$, is a function of the commanded engine load and engine speed

$WA{P}_{cmd}=f_{WAPcmd}\left(L_{cmd},N\right)$

where:

• WAP_cmd is wastegate area percentage command, in percent.

• L_cmd=L is commanded engine load, dimensionless.

• N is engine speed, in rpm.

Load breakpoints, f_wap_ld_bpt — Breakpoints

[0.2 0.275 0.35 0.425 0.5 0.575 0.65 0.725 0.8 0.875 0.95 1.025 1.1 1.175 1.25] (default) | vector

Load breakpoints, dimensionless.

Speed breakpoints, f_wap_n_bpt — Breakpoints, rpm

[750 1054 1357 1661 1964 2268 2571 2875 3179 3482 3786 4089 4393 4696 5000] (default) | vector

Speed breakpoints, in rpm.

Intake cam phaser angle, f_icp — Lookup table

array

The intake cam phaser angle command lookup table, $f_{ICPCMD}$, is a function of the engine load and engine speed

${\phi }_{ICPCMD}=f_{ICPCMD}\left(L_{est},N\right)$

where:

• ${\phi }_{ICPCMD}$ is commanded intake cam phaser angle, in crank degrees advance from park.

• L_est=L is estimated engine load, dimensionless.

• N is engine speed, in rpm.

Exhaust cam phaser angle, f_ecp — Lookup table

array

The exhaust cam phaser angle command lookup table, $f_{ECPCMD}$, is a function of the engine load and engine speed

${\phi }_{ECPCMD}=f_{ECPCMD}\left(L_{est},N\right)$

where:

• ${\phi }_{ECPCMD}$ is commanded exhaust cam phaser angle, in crank degrees retard from park.

• L_est=L is estimated engine load, dimensionless.

• N is engine speed, in rpm.

Load breakpoints, f_cp_ld_bpt — Breakpoints

[0.2 0.275 0.35 0.425 0.5 0.575 0.65 0.725 0.8 0.875 0.95 1.025 1.1 1.175 1.25] (default) | vector

Load breakpoints, dimensionless.

Speed breakpoints, f_cp_n_bpt — Breakpoints

[750 1054 1357 1661 1964 2268 2571 2875 3179 3482 3786 4089 4393 4696 5000] (default) | vector

Speed breakpoints, in rpm.

Commanded EGR percent, f_egrpct_cmd — Lookup table

array

The EGR percent command, EGR_pct,cmd, lookup table is a function of estimated engine load and engine speed

$$EG{R}_{pct,cmd}=f_{EGRpct,cmd}(L_{est},N)$$

where:

• EGR_pct,cmd is commanded EGR percent, dimensionless.

• L_est=L is estimated engine load, dimensionless.

• N is engine speed, in rpm.

Load breakpoints, f_egrpct_ld_bpt — Breakpoints

[0 0.2 0.275 0.35 0.425 0.5 0.575 0.65 0.725 0.8 0.875 0.95 1.025 1.1 1.175 1.25] (default) | vector

Engine load breakpoints, L, dimensionless.

Speed breakpoints, f_egrpct_n_bpt — Breakpoints

[750 1054 1357 1661 1964 2268 2571 2875 3179 3482 3786 4089 4393 4696 5000] (default) | vector

Engine speed breakpoints, N, in rpm.

EGR valve area percent, f_egr_areapct_cmd — Lookup table

array

The EGR area percent command, EGRap_cmd, lookup table is a function of the normalized mass flow and pressure ratio

$$EGRa{p}_{cmd}=f_{EGRap,cmd}\left(\frac{{\dot{m}}_{EGRstd,cmd}}{{\dot{m}}_{EGRstd,max}},\frac{P_{out,EGR}}{P_{in,EGR}}\right)$$

where:

• EGRap_cmd is commanded EGR area percent, dimensionless.

• $$\frac{{\dot{m}}_{EGRstd,cmd}}{{\dot{m}}_{EGRstd,max}}$$ is the normalized mass flow, dimensionless.

• $$\frac{P_{out,EGR}}{P_{in,EGR}}$$ is the pressure ratio, dimensionless.

Open EGR valve standard flow, f_egr_max_stdflow — Breakpoints

[74.87 74.87 74.74 74.39 73.81 72.98 71.91 70.58 68.97 67.06 64.84 62.25 59.27 55.81 51.79 47.07 36.33 24.22 12.11 0] (default) | vector

Maximum standard EGR valve mass flow breakpoints, $${\dot{m}}_{EGRstd,max}$$, in N·m.

Normalized EGR valve standard flow breakpoints, f_egr_areapct_nrmlzdflow_bpt — Breakpoints

[0 0.03448 0.06897 0.1034 0.1379 0.1724 0.2069 0.2414 0.2759 0.3103 0.3448 0.3793 0.4138 0.4483 0.4828 0.5172 0.5517 0.5862 0.6207 0.6552 0.6897 0.7241 0.7586 0.7931 0.8276 0.8621 0.8966 0.931 0.9655 1] (default) | vector

Normalized mass flow breakpoints, $$\frac{{\dot{m}}_{EGRstd,cmd}}{{\dot{m}}_{EGRstd,max}}$$, dimensionless.

EGR valve pressure ratio breakpoints, f_egr_areapct_pr_bpt — Breakpoints

vector

Pressure ratio breakpoints, $$\frac{P_{out,EGR}}{P_{in,EGR}}$$, dimensionless.

Fuel

Injector slope, Sinj — Slope

6.452 (default) | scalar

Fuel injector slope, $S_{inj}$, in mg/ms.

Stoichiometric air-fuel ratio, afr_stoich — Ratio

14.6 (default) | scalar

Stoichiometric air-fuel ratio, AFR_stoich.

Relative air-fuel ratio lambda, f_lamcmd — Air-fuel-ratio (AFR) lookup table

array

The commanded lambda, $${\lambda }_{cmd}$$, lookup table is a function of estimated engine load and measured engine speed

${\lambda }_{cmd}=f_{\lambda cmd}\left(L_{est},N\right)$

where:

• $${\lambda }_{cmd}$$ is commanded relative AFR, dimensionless.

• L_est=L is estimated engine load, dimensionless.

• N is engine speed, in rpm.

Dependencies

To create this parameter, on the Fuel tab, on the Open-loop fuel pane, clear Input lambda.

Load breakpoints, f_lamcmd_ld_bpt — Breakpoints

[0.2 0.275 0.35 0.425 0.5 0.575 0.65 0.725 0.8 0.875 0.95 1.025 1.1 1.175 1.25] (default) | vector

Load breakpoints, dimensionless.

Dependencies

To create this parameter, on the Fuel tab, on the Open-loop fuel pane, clear Input lambda.

Speed breakpoints, f_lamcmd_n_bpt — Breakpoints

[750 1054 1357 1661 1964 2268 2571 2875 3179 3482 3786 4089 4393 4696 5000] (default) | vector

Speed breakpoints, in rpm.

Dependencies

To create this parameter, on the Fuel tab, on the Open-loop fuel pane, clear Input lambda.

Engine startup lambda enrichment delta vs coolant temperature, f_startup_lambda_delta — Lookup table

[0.5 0.3 0.2 0] (default) | vector

Engine startup lambda enrichment delta as a function of coolant temperature, dimensionless.

The SI Controller block uses this parameter to account for the extra fuel delivered to the spark-ignition (SI) engine during startup. If the engine speed is greater than the Engine cranking speed parameter, the SI Controller block enriches the optimal relative air-fuel ratio (lambda) with an exponentially decaying delta lambda. To initialize the delta lambda, the block uses the Engine startup lambda enrichment delta vs coolant temperature parameter to create a lambda enrichment table that is a function of the engine coolant temperature. The delta lambda exponentially decays to zero based on a time constant specified with the Engine startup lambda enrichment delta time constant vs coolant temperature parameter.

Dependencies

To create this parameter, on the Fuel tab, on the Open-loop fuel pane, clear Input lambda.

Engine startup lambda enrichment delta time constant vs coolant temperature, f_startup_lambda_delta_timecnst — Lambda time constant

[90 40 12 0] (default) | vector

Engine startup lambda enrichment delta time constant versus coolant temperature, in s.

The SI Controller block uses this parameter to account for the extra fuel delivered to the spark-ignition (SI) engine during startup. If the engine speed is greater than the Engine cranking speed parameter, the SI Controller block enriches the optimal relative air-fuel ratio (lambda) with an exponentially decaying delta lambda. To initialize the delta lambda, the block uses the Engine startup lambda enrichment delta vs coolant temperature parameter to create a lambda enrichment table that is a function of the engine coolant temperature. The delta lambda exponentially decays to zero based on a time constant specified with the Engine startup lambda enrichment delta time constant vs coolant temperature parameter.

Dependencies

To create this parameter, on the Fuel tab, on the Open-loop fuel pane, clear Input lambda.

Engine startup coolant temperature breakpoints, f_startup_ect_bpt — Breakpoints

[-40 0 20 50] (default) | vector

Engine startup coolant temperature breakpoints, in C.

The SI Controller block uses this parameter to account for the extra fuel delivered to the spark-ignition (SI) engine during startup. If the engine speed is greater than the Engine cranking speed parameter, the SI Controller block enriches the optimal relative air-fuel ratio (lambda) with an exponentially decaying delta lambda. To initialize the delta lambda, the block uses the Engine startup lambda enrichment delta vs coolant temperature parameter to create a lambda enrichment table that is a function of the engine coolant temperature. The delta lambda exponentially decays to zero based on a time constant specified with the Engine startup lambda enrichment delta time constant vs coolant temperature parameter.

Dependencies

To create this parameter, on the Fuel tab, on the Open-loop fuel pane, clear Input lambda.

Closed-loop feedback — Minimize commanded AFR error

off (default) | on

Select option to minimize the commanded air-fuel-ratio (lambda), λ_cmd error.

Dependencies

Selecting this parameter enables these parameters:

• Closed-loop fuel proportional gain, ClsdLpFuelPGain

• Closed-loop fuel integral gain, ClsdLpFuelIGain

• Closed-loop fuel integrator limit, ClsdLpFuelIntgLmt

• Lambda dither amplitude, LambdaDitherAmp

• Lambda dither frequency, LambdaDitherFrq

• Oxygen sensor stoichiometric reset voltage, O2ResetStoichVoltSen

• Oxygen sensor minimum voltage reset, O2ResetMinVoltSen

• Oxygen sensor maximum voltage reset, O2ResetMaxVoltSen

• Oxygen sensor voltage learn update period, O2LearnUpdatePerSen

• Oxygen sensor voltage amplitude minimum, O2AmpMinVoltSen

• Oxygen sensor ready voltage, O2ReadyVoltSen

• Oxygen sensor not ready voltage, O2NotReadyVoltSen

Dither — Model catalytic conversion efficiency

off (default) | on

Configure the block to model dither. For open-loop analysis, select this option to tune for maximum catalytic conversion efficiency.

Dependencies

By default, selecting Closed-loop feedback configures the block to model dither.

To enable this parameter for open-loop air-fuel-ratio (lambda) commands, clear Closed-loop feedback.

Selecting this parameter enables these parameters:

• Lambda dither amplitude, LambdaDitherAmp

• Lambda dither frequency, LambdaDitherFrq

Closed-loop fuel proportional gain, ClsdLpFuelPGain — Proportional gain

0.005 (default) | scalar

Closed-loop fuel proportional gain, dimensionless.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Closed-loop fuel integral gain, ClsdLpFuelIGain — Integral gain

0.05 (default) | scalar

Closed-loop fuel integral gain, dimensionless.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Closed-loop fuel integrator limit, ClsdLpFuelIntgLmt — Integrator limit

0.2 (default) | scalar

Closed-loop fuel integrator limit, dimensionless.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Lambda dither amplitude, LambdaDitherAmp — Amplitude

0.03 (default) | scalar

Lambda dither amplitude, dimensionless.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select either Closed-loop feedback or Dither.

Lambda dither frequency, LambdaDitherFrq — Frequency

0.75 (default) | scalar

Lambda dither frequency, in Hz.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select either Closed-loop feedback or Dither.

Oxygen sensor stoichiometric reset voltage, O2ResetStoichVoltSen — Closed-loop AFR control

2500 (default) | scalar

Oxygen sensor stoichiometric reset voltage, O2ResetStoichVoltSen, in mV.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Oxygen sensor minimum voltage reset, O2ResetMinVoltSen — Closed-loop AFR control

0 (default) | scalar

Oxygen sensor minimum voltage reset, O2ResetMinVoltSen, in mV.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Oxygen sensor maximum voltage reset, O2ResetMaxVoltSen — Closed-loop AFR control

5000 (default) | scalar

Oxygen sensor maximum voltage reset, O2ResetMaxVoltSen, in mV.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Oxygen sensor voltage learn update period, O2LearnUpdatePerSen — Closed-loop AFR control

4 (default) | scalar

Oxygen sensor voltage learn update period, O2LearnUpdatePerSen, in mV.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Oxygen sensor voltage amplitude minimum, O2AmpMinVoltSen — Closed-loop AFR control

250 (default) | scalar

Oxygen sensor voltage amplitude minimum, O2AmpMinVoltSen, in mV.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Oxygen sensor ready voltage, O2ReadyVoltSen — Closed-loop AFR control

1150 (default) | scalar

Oxygen sensor ready voltage, O2ReadyVoltSen, in mV.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Oxygen sensor not ready voltage, O2NotReadyVoltSen — Closed-loop AFR control

1950 (default) | scalar

Oxygen sensor not ready voltage, O2NotReadyVoltSen, in mV.

Dependencies

To enable this parameter, on the Fuel tab, on the Closed-loop fuel pane, select Closed-loop feedback.

Spark

Spark advance table, f_sa — Lookup table

array

The spark advance lookup table is a function of estimated load and engine speed.

$SA=f_{SA}\left(L_{est},N\right)$

where:

• SA is spark advance, in crank advance degrees.

• L_est=L is estimated engine load, dimensionless.

• N is engine speed, in rpm.

Load breakpoints, f_sa_ld_bpt — Breakpoints

[0.2 0.275 0.35 0.425 0.5 0.575 0.65 0.725 0.8 0.875 0.95 1.025 1.1 1.175 1.25] (default) | vector

Load breakpoints, dimensionless.

Speed breakpoints, f_sa_n_bpt — Breakpoints

[750 1054 1357 1661 1964 2268 2571 2875 3179 3482 3786 4089 4393 4696 5000] (default) | vector

Speed breakpoints, in rpm.

Idle Speed

Target idle speed, N_idle — Speed

750 (default) | scalar

Target idle speed, N_idle, in rpm.

Enable torque command limit, Trq_idlecmd_enable — Torque

1 (default) | scalar

Torque to enable the idle speed controller, Trq_{idlecmd,enable}, in N·m.

Maximum torque command, Trq_idlecmd_max — Torque

50 (default) | scalar

Maximum idle controller commanded torque, Trq_idlecmd,max, in N·m.

Proportional gain, Kp_idle — PI Controller

0.05 (default) | scalar

Proportional gain for idle speed control, K_p,idle, in N·m/rpm.

Integral gain, Ki_idle — PI Controller

0.2 (default) | scalar

Integral gain for idle speed control, K_i,idle, in N·m/(rpm·s).

Rev-limiter speed threshold — Engine speed limit

scalar

Engine speed limit, N_lim, in rpm.

If the engine speed, N, exceeds the engine speed limit, N_lim, the block sets the commanded engine torque to 0.

To smoothly transition the torque command to 0 as the engine speed approaches the speed limit, the block implements a lookup table multiplier. The lookup table multiplies the torque command by a value that ranges from 0 (engine speed exceeds limit) to 1 (engine speed does not exceed the limit).

Engine cranking speed, CrankSpeed — Engine speed

150 (default) | scalar

Engine cranking speed, in rpm.

Stop-Start

Enable Engine Stop-Start — Select to enable the engine stop-start logic

off (default) | on

Select to enable the engine stop-start logic. Selecting this option will activate additional parameters to modify the behavior of the Engine Stop-Start block.

External Enable Port — Create input port

off (default) | on

Select to add a port to the engine controller block which enables or disables the stop-start logic.

Dependencies

To enable this parameter, on the Stop-Start tab, select Enable Engine Stop-Start.

Engine stop time, EngStopTime [s] — Engine stop time

5 (default) | scalar

Engine stop time for the stop-start logic, in s.

Dependencies

To enable this parameter, on the Stop-Start tab, select Enable Engine Stop-Start.

Catalyst light off time, CatLightOffTime [s] — Catalyst light off time

0 (default) | scalar

Catalyst light off time for the stop-start logic, in s.

Dependencies

To enable this parameter, on the Stop-Start tab, select Enable Engine Stop-Start.

Sample time, Ts [s] — Sample time

0.01 (default) | scalar

Sample time for the stop-start logic, in s.

Dependencies

To enable this parameter, on the Stop-Start tab, select Enable Engine Stop-Start.

Estimation

Air

Number of cylinders, NCyl — Engine cylinders

4 (default) | scalar

Number of engine cylinders, $N_{cyl}$.

Crank revolutions per power stroke, Cps — Revolutions per stroke

2 (default) | scalar

Crankshaft revolutions per power stroke, $$Cps$$, in rev/stroke.

Total displaced volume, Vd — Volume

0.0015 (default) | scalar

Displaced volume, $V_d$, in m^3.

Ideal gas constant air, Rair — Constant

287 (default) | scalar

Ideal gas constant, $R_{air}$, in J/(kg·K).

Air standard pressure, Pstd — Pressure

101325 (default) | scalar

Standard air pressure, $P_{std}$, in Pa.

Air standard temperature, Tstd — Temperature

293.15 (default) | scalar

Standard air temperature, $T_{std}$, in K.

Speed-density volumetric efficiency, f_nv — Lookup table

array

The engine volumetric efficiency lookup table, $f_{{\eta }_v}$, is a function of intake manifold absolute pressure and engine speed

${\eta }_v=f_{{\eta }_v}(MAP,N)$

where:

• ${\eta }_v$ is engine volumetric efficiency, dimensionless.

• MAP is intake manifold absolute pressure, in KPa.

• N is engine speed, in rpm.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Simple Speed-Density.

Speed-density intake manifold pressure breakpoints, f_nv_prs_bpt — Breakpoints

[31 40.64 50.29 59.93 69.57 79.21 88.86 98.5 108.1 117.8 127.4 137.1 146.7 156.4 166] (default) | vector

Intake manifold pressure breakpoints for speed-density volumetric efficiency lookup table, in KPa.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Simple Speed-Density.

Speed-density engine speed breakpoints, f_nv_n_bpt — Breakpoints

[750 1054 1357 1661 1964 2268 2571 2875 3179 3482 3786 4089 4393 4696 5000] (default) | vector

Engine speed breakpoints for speed-density volumetric efficiency lookup table, in rpm.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Simple Speed-Density.

Cylinder volume at intake valve close table, f_vivc — 2-D lookup table

array

The cylinder volume at intake valve close table (IVC), $f_{Vivc}$ is a function of the intake cam phaser angle

$V_{IVC}=f_{Vivc}({\phi }_{ICP})$

where:

• $$V_{IVC}$$ is cylinder volume at IVC, in L.

• ${\phi }_{ICP}$ is intake cam phaser angle in crank degrees of advance relative to the intake phaser park position.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Engine speed breakpoints, f_tm_corr_n_bpt — Breakpoints

[750 973.7 1197 1421 1645 1868 2092 2316 2539 2763 2987 3211 3434 3658 3882 4105 4329 4553 4776 5000] (default) | vector

Engine speed breakpoints, in rpm.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Cylinder volume intake cam phase breakpoints, f_vivc_icp_bpt — Breakpoints

[0 2.632 5.263 7.895 10.53 13.16 15.79 18.42 21.05 23.68 26.32 28.95 31.58 34.21 36.84 39.47 42.11 44.74 47.37 50] (default) | vector

Cylinder volume at intake valve close table breakpoints.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Cylinder trapped mass correction factor, f_tm_corr — Lookup table

array

The trapped mass correction factor table, $f_{TMcorr}$, is a function of the normalized density and engine speed

$T{M}_{corr}=f_{TMcorr}({\rho }_{norm}, N)$

where:

• $T{M}_{corr}$, is trapped mass correction multiplier, dimensionless.

• ${\rho }_{norm}$ is normalized density, dimensionless.

• N is engine speed, in rpm.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Normalized density breakpoints, f_tm_corr_nd_bpt — Breakpoints

[0.3 0.3895 0.4789 0.5684 0.6579 0.7474 0.8368 0.9263 1.016 1.105 1.195 1.284 1.374 1.463 1.553 1.642 1.732 1.821 1.911 2] (default) | vector

Normalized density breakpoints.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Intake mass flow, f_mdot_intk — Lookup table

array

The phaser intake mass flow model lookup table is a function of exhaust cam phaser angles and trapped air mass flow

${\dot{m}}_{intkideal}=f_{intkideal}({\phi }_{ECP},T{M}_{flow})$

where:

• ${\dot{m}}_{intkideal}$ is engine intake port mass flow at arbitrary cam phaser angles, in g/s.

• ${\phi }_{ECP}$ is exhaust cam phaser angle in crank degrees of retard relative to the exhaust phaser park position.

• $T{M}_{flow}$ is flow rate equivalent to corrected trapped mass at the current engine speed, in g/s.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Exhaust cam phase breakpoints, f_mdot_air_ecp_bpt — Breakpoints

[0 2.632 5.263 7.895 10.53 13.16 15.79 18.42 21.05 23.68 26.32 28.95 31.58 34.21 36.84 39.47 42.11 44.74 47.37 50] (default) | vector

Exhaust cam phaser breakpoints for air mass flow lookup table.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Trapped mass flow breakpoints, f_mdot_trpd_bpt — Breakpoints

[0 5.79 11.58 17.37 23.16 28.95 34.74 40.53 46.32 52.11 57.89 63.68 69.47 75.26 81.05 86.84 92.63 98.42 104.2 110] (default) | vector

Trapped mass flow breakpoints for air mass flow lookup table.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Air mass flow correction factor, f_mdot_air_corr — Lookup table

array

The intake air mass flow correction lookup table, $f_{aircorr}$, is a function of ideal load and engine speed

${\dot{m}}_{air}={\dot{m}}_{intkideal}{f}_{aircorr}(L_{ideal},N)$

where:

• $L_{ideal}$ is engine load (normalized cylinder air mass) at arbitrary cam phaser angles, uncorrected for final steady-state cam phaser angles, dimensionless.

• N is engine speed, in rpm.

• ${\dot{m}}_{air}$ is engine intake air mass flow final correction at steady-state cam phaser angles, in g/s.

• ${\dot{m}}_{intkideal}$ is engine intake port mass flow at arbitrary cam phaser angles, in g/s.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Engine load breakpoints for air mass flow correction, f_mdot_air_corr_ld_bpt — Breakpoints

vector

Engine load breakpoints for air mass flow final correction.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

Engine speed breakpoints for air mass flow correction, f_mdot_air_n_bpt — Breakpoints

[750 973.7 1197 1421 1645 1868 2092 2316 2539 2763 2987 3211 3434 3658 3882 4105 4329 4553 4776 5000] (default) | vector

Engine speed breakpoints for air mass flow final correction.

Dependencies

To enable this parameter, for the Air mass flow estimation model parameter, select Dual Variable Cam Phasing.

EGR flow time constant, tau_egr — Constant

0.2 (default) | scalar

EGR flow time constant, τ_EGR, in s.

Intake system pressure ratio table, f_intksys_stdflow_pr — Table

array

The pressure ratio is a function of the standard mass flow

$$\frac{P_{out,EGR}}{P_{amb}}=f_{intksys,pr}({\dot{m}}_{air,std})$$

where:

• $${\dot{m}}_{air,std}$$ is standard mass flow, in g/s.

• $$\frac{P_{out,EGR}}{P_{amb}}$$ is pressure ratio, dimensionless.

Standard mass flow rate breakpoints for intake pressure ratio, f_intksys_stdflow_bpt — Breakpoints

[0 29.67 59.34 89.01 117.8 144.1 155.7 166 175.2 183.3 190.7 197 202.7 207.7 212.2 216.1 219.4 222.2 224.5 226.4] (default) | vector

Standard mass flow, $${\dot{m}}_{air,std}$$, in g/s.

EGR valve standard mass flow rate, f_egr_stdflow — Table

array

The EGR valve standard mass flow lookup table is a function of EGR valve area percent and the pressure ratio

$${\dot{m}}_{EGR,std}=f_{EGR,std}\left(EGRap,\frac{P_{out,EGR}}{P_{in,EGR}}\right)$$

where:

• $${\dot{m}}_{EGR,std}$$ is EGR valve standard mass flow, dimensionless.

• EGRap is EGR valve flow area percent, in percent.

• $$\frac{P_{out,EGR}}{P_{in,EGR}}$$ is the pressure ratio, dimensionless.

EGR valve standard flow pressure ratio breakpoints, f_egr_stdflow_pr_bpt — Breakpoints

vector

EGR valve standard flow pressure ratio,$$\frac{P_{out,EGR}}{P_{in,EGR}}$$, dimensionless.

EGR valve standard flow area percent breakpoints, f_egr_stdflow_egrap_bpt — Breakpoints

[0;5;10;15;20;25;30;35;40;45;50;55;60;65;70;75;80;85;90;95;100] (default) | vector

EGR valve flow area percent, EGRap, in percent.

Torque

Torque table, f_tq_nl — Lookup table

[L x N] array

For the simple torque lookup table model, the SI engine uses a lookup table map that is a function of engine speed and load, $T_{brake}=f_{TnL}(L,N)$, where:

• $T_{brake}$ is engine brake torque after accounting for spark advance, AFR, and friction effects, in N·m.

• L is engine load, as a normalized cylinder air mass, dimensionless.

• N is engine speed, in rpm.

The simple torque lookup model assumes that the calibration has negative torque values to indicate the non-firing engine load (L) versus speed (N) condition. The calibrated table (L-by-N) contains the non-firing data in the first table row (1-by-N). When the fuel delivered to the engine is zero, the model uses the data in the first table row (1-by-N) at or above 100 AFR. 100 AFR results from fuel cutoff or very lean operation where combustion cannot occur.

Dependencies

To enable this parameter, for the Torque model parameter, select Simple Torque Lookup.

Torque table load breakpoints, f_tq_nl_l_bpt — Breakpoints

[0.2 0.275 0.35 0.425 0.5 0.575 0.65 0.725 0.8 0.875 0.95 1.025 1.1 1.175 1.25] (default) | vector | [1 x L] vector

Engine load breakpoints, L, dimensionless.

Dependencies

To enable this parameter, for the Torque model parameter, select Simple Torque Lookup.

Torque table speed breakpoints, f_tq_nl_n_bpt — Breakpoints

[750 1053.57142857143 1357.14285714286 1660.71428571429 1964.28571428571 2267.85714285714 2571.42857142857 2875 3178.57142857143 3482.14285714286 3785.71428571429 4089.28571428571 4392.85714285714 4696.42857142857 5000] (default) | vector | [1 x N] vector

Engine speed breakpoints, N, in rpm.

Dependencies

To enable this parameter, for the Torque model parameter, select Simple Torque Lookup.

Crank angle pressure and torque — Enable Crank angle signals

off (default) | on

If you select Crank angle pressure and torque on the block Torque tab, you can:

• Simulate advanced closed-loop engine controls in desktop simulations and on HIL bench, based on cylinder pressure recorded from a model or laboratory test as a function of crank angle.

• Simulate driveline vibrations downstream of the engine due to high-frequency crankshaft torsionals.

• Simulate engine misfires due to lean operation or spark plug fouling by using the injector pulse width input.

• Simulate cylinder deactivation effect (closed intake and exhaust valves, no injected fuel) on individual cylinder pressures, mean-value airflow, mean-value torque, and crank-angle-based torque.

• Simulate the fuel-cut effect on individual cylinder pressure, mean-value torque, and crank-angle-based torque.

Dependencies

To enable this parameter, set Torque model to Torque Structure.

Cylinder pressure, f_crk_prs — Cylinder pressure table

L x M x N array

Cylinder pressure table Prs, as a function of speed N, load L, and crank angle M, in Pa.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure. Select Crank angle pressure and torque.

Brake torque, f_crk_btq — Brake torque table

L x M x N array

Brake torque table T_brake, as a function of speed N, load L, and crank angle M, in N·m.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure. Select Crank angle pressure and torque.

Speed breakpoints, f_crk_n_bpt — Speed breakpoints

[750 5000] (default) | 1 x N vector

Speed breakpoints, N, in rpm.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure. Select Crank angle pressure and torque.

Load breakpoints, f_crk_l_bpt — Load breakpoints

[0.2 1.4] (default) | 1 x L vector

Load breakpoints, L. No dimension.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure. Select Crank angle pressure and torque.

Crank angle breakpoints, f_crk_ang_bpt — Crank angle breakpoints

[60 660] (default) | 1 x M vector

Crank angle breakpoints, M, in deg.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure. Select Crank angle pressure and torque.

TDC compression angles by cylinder, f_crk_tdc_ang — TDC compression angles by cylinder

[0 540 180 360] (default) | vector

Top dead center (TDC) compression angles by cylinder, in deg.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure. Select Crank angle pressure and torque.

Inner torque table, f_tq_inr — Lookup table

array

The inner torque lookup table, $f_{Tqinr}$, is a function of engine speed and engine load, $T{q}_{inr}=f_{Tqinr}(L,N)$, where:

• $T{q}_{inr}$ is inner torque based on gross indicated mean effective pressure, in N·m.

• L is engine load at arbitrary cam phaser angles, corrected for final steady-state cam phaser angles, dimensionless.

• N is engine speed, in rpm.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Friction torque table, f_tq_fric — Lookup table

array

The friction torque lookup table, $f_{Tfric}$, is a function of engine speed and engine load, $$T_{fric}=f_{Tfric}\left(L,N\right)$$, where:

• $T_{fric}$ is friction torque offset to inner torque, in N·m.

• L is engine load at arbitrary cam phaser angles, corrected for final steady-state cam phaser angles, dimensionless.

• N is engine speed, in rpm.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Engine temperature modifier on friction torque, f_fric_temp_mod — Lookup table

[3.96 3.22 2.56 2.26 2.11 2 1.9 1.83 1.76 1.7 1.65 1.6 1.55 1.49 1.44 1.41 1.38 1.35 1.32 1.3 1.27 1.25 1.24 1.21 1.2 1.18 1.16 1.15 1.13 1.12 1.11 1.1 1.09 1.08 1.07 1.06 1.05 1.05 1.04 1.03 1.02 1.02 1.01 1.01 1 1 1 0.999 0.997 0.995 0.993 0.991 0.989 0.987] (default) | vector | vector

Engine temperature modifier on friction torque, ƒ_fric,temp, dimensionless.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Engine temperature modifier breakpoints, f_fric_temp_bpt — Breakpoints

[274 276 278 280 282 284 286 288 290 292 294 296 298 300 302 304 306 308 310 312 314 316 318 320 322 324 326 328 330 332 334 336 338 340 342 344 346 348 350 352 354 356 358 360 362 364 366 368 370 372 374 376 378 380] (default) | vector | vector

Engine temperature modifier breakpoints, in K.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Pumping torque table, f_tq_pump — Lookup table

array

The pumping torque lookup table, ƒ_Tpump, is a function of engine load and engine speed, Tpump=ƒTpump(L,N), where:

• T_pump is pumping torque, in N·m.

• L is engine load, as a normalized cylinder air mass, dimensionless.

• N is engine speed, in rpm.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Optimal spark table, f_sa_opt — Lookup table

array

The optimal spark lookup table, $f_{SAopt}$, is a function of engine speed and engine load, $S{A}_{opt}=f_{SAopt}(L,N)$, where:

• SA_opt is optimal spark advance timing for maximum inner torque at stoichiometric air-fuel ratio (AFR), in deg.

• L is engine load at arbitrary cam phaser angles, corrected for final steady-state cam phaser angles, dimensionless.

• N is engine speed, in rpm.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Inner torque load breakpoints, f_tq_inr_l_bpt — Breakpoints

[0.2 0.28571 0.37143 0.45714 0.54286 0.62857 0.71429 0.8 0.88571 0.97143 1.0571 1.1429 1.2286 1.3143 1.4] (default) | vector

Inner torque load breakpoints, dimensionless.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Inner torque speed breakpoints, f_tq_inr_n_bpt — Breakpoints

[750 1053.5714 1357.1429 1660.7143 1964.2857 2267.8571 2571.4286 2875 3178.5714 3482.1429 3785.7143 4089.2857 4392.8571 4696.4286 5000] (default) | vector

Inner torque speed breakpoints, in rpm.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Spark efficiency table, f_m_sa — Lookup table

array

The spark efficiency lookup table, $f_{Msa}$, is a function of the spark retard from optimal

$\begin{array}{l}{M}_{sa}=f_{Msa}(\Delta SA)\\ \Delta SA=S{A}_{opt}-SA\end{array}$

where:

• $M_{sa}$ is the spark retard efficiency multiplier, dimensionless.

• $\Delta SA$is the spark retard timing distance from optimal spark advance, in deg.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Spark retard from optimal, f_del_sa_bpt — Breakpoints

[0 0.75 1.5 2.25 3 3.75 4.5 5.25 6 6.75 7.5 8.25 9 9.75 10.5 11.25 12 12.75 13.5 14.25 15 15.75 16.5 17.25 18 18.75 19.5 20.25 21 21.75 22.5 23.25 24 24.75 25.5 26.25 27 27.75 28.5 29.25 30 30.75 31.5 32.25 33 33.75 34.5 35.25 36 36.75 37.5 38.25 39 39.75 40.5 41.25 42 42.75 43.5 44.25 45 45.75 46.5 47.25 48] (default) | vector

Spark retard from optimal inner torque timing breakpoints, in deg.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Lambda efficiency, f_m_lam — Lookup table

array

The lambda efficiency lookup table, $f_{M\lambda }$, is a function of lambda, $M_{\lambda }=f_{M\lambda }(\lambda )$, where:

• $M_{\lambda }$ is the lambda multiplier on inner torque to account for the air-fuel ratio (AFR) effect, dimensionless.

• $\lambda$ is lambda, AFR normalized to stoichiometric fuel AFR, dimensionless.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Lambda breakpoints, f_m_lam_bpt — Breakpoints

[0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 1.05 1.1] (default) | vector

Lambda effect on inner torque lambda breakpoints, dimensionless.

Dependencies

To enable this parameter, for the Torque model parameter, select Torque Structure.

Exhaust

Exhaust temperature table, f_t_exh — Lookup table

array

The exhaust temperature lookup table, $f_{Texh}$, is a function of engine load and engine speed

$T_{exh}=f_{Texh}(L,N)$

where:

• T_exh is engine exhaust temperature, in K.

• L is normalized cylinder air mass or engine load, dimensionless.

• N is engine speed, in rpm.

Load breakpoints, f_t_exh_l_bpt — Breakpoints

[0.2 0.275 0.35 0.425 0.5 0.575 0.65 0.725 0.8 0.875 0.95 1.025 1.1 1.175 1.25] (default) | vector

Engine load breakpoints used for exhaust temperature lookup table.

Speed breakpoints, f_t_exh_n_bpt — Breakpoints

[750 1054 1357 1661 1964 2268 2571 2875 3179 3482 3786 4089 4393 4696 5000] (default) | vector

Engine speed breakpoints used for exhaust temperature lookup table, in rpm.

References

[1] Gerhardt, J., Hönninger, H., and Bischof, H., A New Approach to Functional and Software Structure for Engine Management Systems — BOSCH ME7. SAE Technical Paper 980801, 1998.

[2] Heywood, John B. Internal Combustion Engine Fundamentals. New York: McGraw-Hill, 1988.

[3] Leone, T. Christenson, E., Stein, R., Comparison of Variable Camshaft Timing Strategies at Part Load. SAE Technical Paper 960584, 1996, doi:10.4271/960584.

[4] Liu, F. and Pfeiffer, J., Estimation Algorithms for Low Pressure Cooled EGR in Spark-Ignition Engines. SAE Int. J. Engines 8(4):2015, doi:10.4271/2015-01-1620.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2017a