An Introduction to Battery State of Charge Estimation | How to Estimate Battery State of Charge Using Deep Learning, Part 1
From the series: How to Estimate Battery State of Charge Using Deep Learning
Get an introduction to battery state of charge SOC estimation, its challenges, and motivations for new ways to perform this task. See a review of the state-of-the-art estimation technique and explore the concept of neural networks.
Published: 27 May 2021
Lithium ion batteries play a prominent role in the world because of their high energy and power density, efficiency, cycling capability, low self discharge, and low maintenance. These advantages come along with some drawbacks. Batteries require very careful management to ensure operation within a specified temperature and voltage range. Not only does battery performance strongly depend on temperature, but it is also important not to exceed temperature limits, since the battery does not like to be too hot or too cold. In addition, they need sophisticated model based algorithms for status information. In particular, set of charge estimation, or SOC, the main topic of today's events. And finally, it is also unavoidable that the battery performance will degrade over time, both because of cycling and because of calendar aging. A major development avenue of the battery community involves degradation diagnosis algorithms.
A popular way of modeling batteries with a purpose of system design and battery management is to create an electric thermal analogy for the cells behavior called equivalent circuits. The topology and parameters of the equivalent circuit should allow a user to load it in the same way they would load a battery, and observe the same response a battery would have. This includes voltage drop, relaxation times, and open circuit voltage. All of them, functions of temperature, SOC, and age.
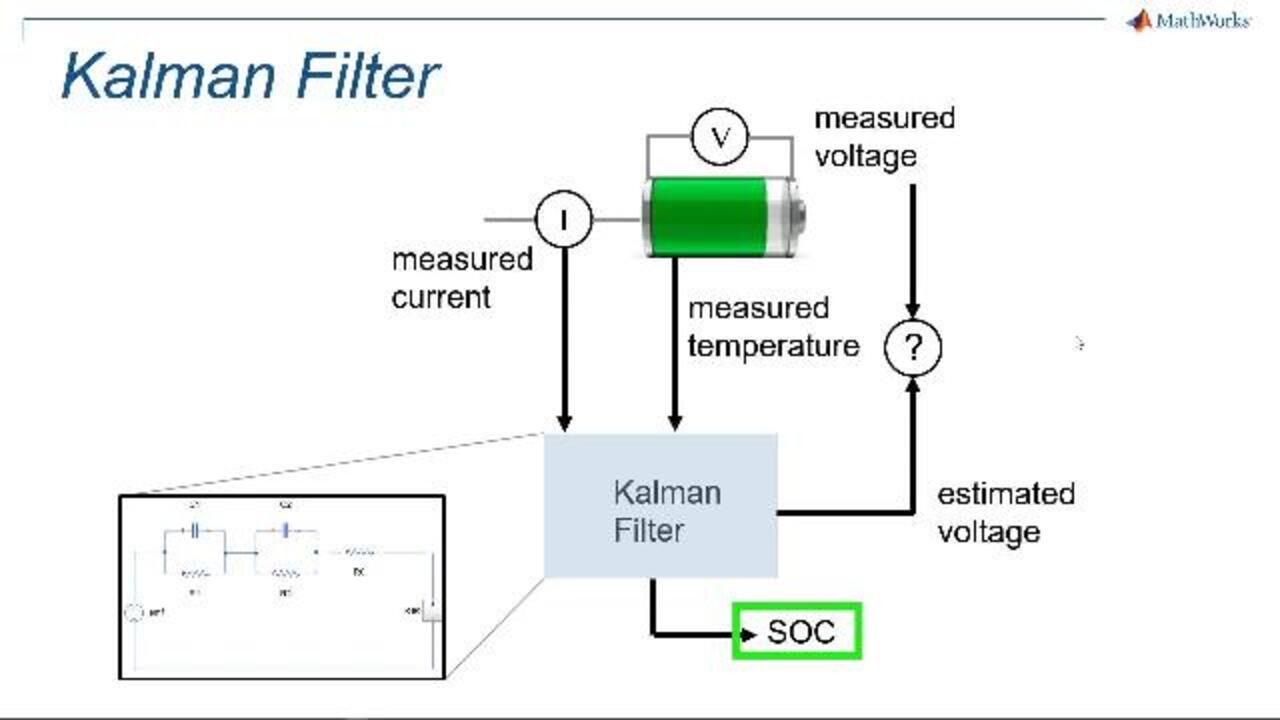
Speaking of SOC, let's see what it is and how we estimate it. SOC is the number between 0 and 1 that indicates the amount of charge available in the cell, relative to the maximum amount of charge defined as the number of empowers extractable from it, when we slowly discharge the battery from to voltage levels, at the reference temperature of 25 degrees. A major challenge with SOC is that it is not directly measurable, but it needs to be inferred based on measurements of voltage, current, and temperature, and the use of a model of the cell. The easiest way to estimate state of charge is integrating current. By definition, the SOC is the integral the currents flowing in and out of the cell over the total capacity. This method simple and computationally cheap. The problem is that any error in the measurement of the current will accumulate, making the same charge diverge from the true value until it would somehow reset it.
A more advanced method of doing this is using observers. For example, a Kalman filter. A Kalman filter is an observer for status information that contains a model of the system under observation, and uses a recursive algorithm that continuously predicts a future state and correct it using measurements performed on the system. In this case, the state of interest is the SOC, or state of charge. And measurements include current, voltage, and temperature. A requirement for the Kalman filter to function correctly is to have an accurate dynamic model of the cell, including dependencies in operating and environmental conditions. Moreover, as a recursive algorithm, it is significantly more resource intensive than simple current integration. So the question many are asking is, is there an alternative to the current state of the art that can provide an accurate estimation of SOC, and at the same time handle that many possible operating conditions, to which a battery cell could be subjected? And that can be used for different cell types with minimal modifications? If so, how efficient would it be as an embedded algorithm?
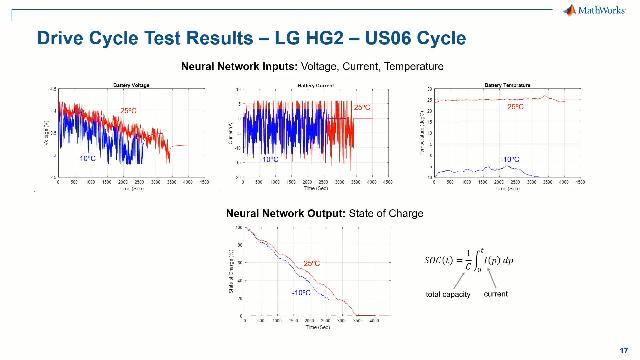
How about using a neural network that takes current voltage and temperature measurements as a function of time, and uses them to predict SOC. Trained with a sufficiently large amount of data, measured under sufficiently varied conditions, would a neural network be able to learn the patterns of change in the measurable quantities of the battery, and link them to an accurate estimation of the set of charge? That is what we're going to be discussing in the next 20 minutes or so, with the authors of this work.