FresnelS and FresnelC
I noticed the many codes on the FEX to compute the Fresnel integrals for real arguments, and it left me wondering how I might try solving this problem in MATLAB for both high accuracy and high efficiency.
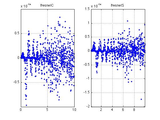
The approach I took yields a maximum error of roughly 1e-14 as far as I could get reasonable values to compare it to. (The screenshot shows the predicted error for a sampling of points.)
I've supplied functions for both the Fresnel sine and cosine integrals, as well as a .pdf file that explains the approach I took.
Evaluate the Fresnel cosine integral C(x) at x = 1.38
>> fresnelC(1.38,0)
ans =
0.562975925772444
Verify the correctness of this value using quadgk.
>> FresnelCObj = @(t) cos(pi*t.^2/2);
>> quadgk(FresnelCObj,0,1.38,'abstol',1e-15')
ans =
0.562975925772444
Now, how fast is fresnelC? Using Steve Eddins timeit code to yield an accurate estimate of the time required, we see that it is reasonably fast for scalar input.
>> timeit(@() fresnelC(1.38))
ans =
0.000193604455833333
More importantly, these functions are properly vectorized. So 1 million evaluations are easy to do, and are much faster than 1 million times the time taken for one evaluation.
>> T = rand(1000000,1);
>> tic
>> FCpred = fresnelC(T);
>> toc
Elapsed time is 0.226884 seconds.
Cite As
John D'Errico (2025). FresnelS and FresnelC (https://se.mathworks.com/matlabcentral/fileexchange/28765-fresnels-and-fresnelc), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired by: Jim McElwaine, Fresnel Sine and Cosine Integrals, Computation of Special Functions, Fresnel integrals, Fresnel Cosine and Sine Integral Function, Fresnel integral, Fresnel integrals, Cornu spiral_Fresnel Integral, Complex Erf (Error Function), Fresnel Integrals, Fresnel Integral
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.