802.11az Positioning Using Super-Resolution Time of Arrival Estimation
This example shows how to estimate the position of a station (STA) in a multipath environment by using a time-of-arrival-based (ToA-based) positioning algorithm defined in the IEEE® 802.11az™ Wi-Fi® standard. The example estimates the ToA by using a multiple signal classification (MUSIC) super-resolution approach, then estimates the two-dimensional position of a STA by using trilateration. The example then evaluates and compares the performance of the positioning algorithm at multiple signal-to-noise ratio (SNR) points.
Introduction
The 802.11az standard [1], commonly referred to as next generation positioning (NGP), enables a STA to identify its position relative to multiple access points (APs). This standard supports two high-efficiency (HE) ranging physical layer (PHY) protocol data unit (PPDU) formats:
HE ranging null data packet (NDP)
HE trigger-based (TB) ranging NDP
The HE ranging NDP and HE TB ranging NDP are the respective analogues of the HE sounding NDP and HE TB feedback NDP PPDU formats, as defined in the 802.11ax™ (Wi-Fi 6) standard. For more information on these HE PPDU formats, see [2].
The HE ranging NDP supports the positioning of one or more users with an optional secure HE long training field (HE-LTF) sequence. The single-user HE ranging waveform contains HE-LTF symbols for a single user, which also support an optional secure HE-LTF sequence. The multi-user HE ranging waveform permits only secure HE-LTF symbols for multiple users. To improve position estimation accuracy, single-user and multi-user waveforms can contain multiple repetitions of the HE-LTF symbols. To parameterize and generate HE ranging NDPs, see the 802.11az Waveform Generation example.
This example simulates an 802.11az network consisting of a STA and multiple APs. To estimate the position of a STA, the network requires a minimum of three APs. The example simulates a ranging measurement exchange for each STA-AP pair, then trilaterates the position of the STA by using these measurements. The example repeats this simulation for multiple iterations and SNR points. This diagram shows the positioning process in a network with one STA and three APs.

Packet Transmission and Reception
This example models the measurement exchange between the STA and APs by performing these steps.
Generate a ranging NDP
Delay the NDP according to a randomly generated distance between the STA and AP, adding fractional and integer sample delay
Pass the waveform through an indoor TGax channel. The example models different channel realizations for different packets
Add additive white Gaussian noise (AWGN) to the received waveform. The example uses the same SNR value for all the links between STA and APs
Perform synchronization and frequency correction on the received waveform
Demodulate the HE-LTF
Estimate the channel frequency response from the HE-LTF
Estimate the distance by using the MUSIC super-resolution algorithm
Combine distance estimates from other STA-AP pairs and trilaterate the position of the STA
This figure illustrates the processing for each STA-AP link.

Distance Ranging
The example performs a distance ranging measurement between the STA and each AP by capturing the timestamps of the NDP. The STA records the time (UL ToD) at which it transmits the uplink NDP (UL NDP). The AP then captures the time (UL ToA) at which it receives the UL NDP and records the time (DL ToD) at which it transmits the downlink NDP (DL NDP). The STA then captures the time (DL ToA) at which it receives the DL NDP. This diagram illustrates the measurement sounding phase between a STA and a single AP [1].

The example estimates the round trip time (RTT), by combining these timestamps.
The example then computes the distance between the STA and AP by using this equation.
, where is speed of light
The example estimates and by using MUSIC super-resolution. To compute these estimates, the example performs these steps [3].
Interpolate across missing subcarriers from the channel frequency response (CFR), assuming uniform subcarrier spacing
Estimate the CFR correlation matrix
Decorrelate the multipaths by using spatial smoothing
Improve the correlation matrix estimate by performing forward-backward averaging. The example assumes that CFR estimates from multiple spatial streams are different CFR snapshots, and uses all the snapshots for correlation matrix estimation.
Run the MUSIC algorithm. Perform eigendecomposition on the correlation matrix to separate it into signal and noise subspaces. Estimate the time-domain delay profile by finding all instances where signal and noise subspaces are orthogonal. The example assumes that the precise signal subspace dimension, equal to the number of multipaths, is known.
Determine the ToA by finding the first peak of the recovered multipaths in the estimated delay profile, assumed to be the direct-line-of-sight (DLOS) path
This diagram illustrates the distance ranging process.

This plot compares the true multipath delay profile and the MUSIC estimated delay profile for a single 802.11az link simulation.
heRangingPlotDelayProfile()

Simulation Parameters
This example performs a ranging and positioning simulation for multiple iterations and SNR points. At each iteration, the AP and the STA exchange multiple uplink and downlink packets. The example estimates the ranging error between the AP and the STA for each iteration by comparing the estimated distance between the AP and the STA with the known distance.
Specify the number of iterations, SNR points, and APs in the networks. To estimate the position of a STA, the network requires a minimum of three APs. For each iteration, use a different random set of AP positions, a different channel realization, and a different AWGN profile. The example generates a cumulative distribution function (CDF) for the absolute ranging error by using the ranging measurements from all iterations and all STA-AP pairs.
numIterations =50; % Number of iterations snrRange =
15:10:35; % SNR points, in dB numAPs =
3; % Number of APs
802.11az Waveform Configuration
Configure waveform generators for each AP and the STA.
chanBW ='CBW20'; % Channel bandwidth numTx =
2; % Number of transmit antennas numRx =
2; % Number of receive antennas numSTS =
2; % Number of space-time streams numLTFRepetitions =
3; % Number of HE-LTF repetitions
Configure the HE ranging NDP parameters of the STA.
cfgSTABase = heRangingConfig;
cfgSTABase.ChannelBandwidth = chanBW;
cfgSTABase.NumTransmitAntennas = numTx;
cfgSTABase.SecureHELTF = true;
cfgSTABase.User{1}.NumSpaceTimeStreams = numSTS;
cfgSTABase.User{1}.NumHELTFRepetitions = numLTFRepetitions;Configure the HE ranging NDP parameters of the APs.
cfgAPBase = cell(1,numAPs); for iAP = 1:numAPs cfgAPBase{iAP} = heRangingConfig; cfgAPBase{iAP}.ChannelBandwidth = chanBW; cfgAPBase{iAP}.NumTransmitAntennas = numTx; cfgAPBase{iAP}.SecureHELTF = true; cfgAPBase{iAP}.User{1}.NumSpaceTimeStreams = numSTS; cfgAPBase{iAP}.User{1}.NumHELTFRepetitions = numLTFRepetitions; end ofdmInfo = wlanHEOFDMInfo('HE-LTF',chanBW,cfgSTABase.GuardInterval); sampleRate = wlanSampleRate(chanBW);
Channel Configuration
Configure the WLAN TGax multipath channel by using the wlanTGaxChannel System object™. This System object can generate a channel with a dominant direct path, in which the DLOS path is the strongest path, or a channel with a non-dominant direct path, for which the DLOS path is present, but not the strongest path.
delayProfile ='Model-B'; % TGax channel multipath delay profile carrierFrequency = 5e9; % Carrier frequency, in Hz speedOfLight = physconst('lightspeed'); chanBase = wlanTGaxChannel; chanBase.DelayProfile = delayProfile; chanBase.NumTransmitAntennas = numTx; chanBase.NumReceiveAntennas = numRx; chanBase.SampleRate = sampleRate; chanBase.CarrierFrequency = carrierFrequency; chanBase.ChannelBandwidth = chanBW; chanBase.PathGainsOutputPort = true; chanBase.NormalizeChannelOutputs = false;
Get channel filter delay and the number of paths
chBaseInfo = info(chanBase); chDelay = chBaseInfo.ChannelFilterDelay; numPaths = size(chBaseInfo.PathDelays,2);
Ranging Measurement
Run a ranging simulation with multiple iterations for all STA-AP pairs. Display the ranging mean absolute error (MAE) and the ranging error CDF for each SNR point.
delayULDL = 16e-6; % Time delay between UL NDP ToA and DL NDP ToD, in seconds numSNR = numel(snrRange); distEst = zeros(numAPs,numIterations,numSNR); % Estimated distance distance = zeros(numAPs,numIterations,numSNR); % True distance positionSTA = zeros(2,numIterations,numSNR); % Two-dimensional position of the STA positionAP= zeros(2,numAPs,numIterations,numSNR); % Two-dimensional positions of the APs per = zeros(numSNR,1); % Packet error rate (PER) %parfor isnr = 1:numSNR % Use 'parfor' to speed up the simulation for isnr = 1:numSNR % Use a separate channel and waveform configuration object for each parfor stream chan = chanBase; cfgAP = cfgAPBase; cfgSTA = cfgSTABase; % Initialize ranging error and total failed packet count variables rangingError = 0; failedPackets = 0; % Set random substream index per iteration to ensure that each % iteration uses a repeatable set of random numbers stream = RandStream('combRecursive','Seed',123456); stream.Substream = isnr; RandStream.setGlobalStream(stream); % Define the SNR per active subcarrier to account for noise energy in nulls snrVal = snrRange(isnr) - 10*log10(ofdmInfo.FFTLength/ofdmInfo.NumTones); for iter = 1:numIterations % Generate random AP positions [positionSTA(:,iter,isnr),positionAP(:,:,iter,isnr),distanceAllAPs] = heGeneratePositions(numAPs); distance(:,iter,isnr) = distanceAllAPs; % Range-based delay delay = distance(:,iter,isnr)/speedOfLight; sampleDelay = delay*sampleRate; % Loop over the number of APs for ap = 1:numAPs linkType = ["Uplink","Downlink"]; % ToD of UL NDP (t1) todUL = randsrc(1,1,0:1e-9:1e-6); % Loop for both UL and DL transmission numLinks = numel(linkType); txTime = zeros(1,numLinks); for l = 1:numLinks if linkType(l) == "Uplink" % STA to AP cfgSTA.UplinkIndication = 1; % For UL % Generate a random secure HE-LTF octets for the exchange numOctets = numSecureHELTFOctets(cfgSTA); cfgSTA.User{1}.SecureHELTFOctets = dec2hex(randsrc(1,2*numOctets(1),(0:15)))'; cfg = cfgSTA; else % AP to STA % Generate a random secure HE-LTF octets for the exchange numOctets = numSecureHELTFOctets(cfgAP{ap}); cfgAP{ap}.User{1}.SecureHELTFOctets = dec2hex(randsrc(1,2*numOctets(1),(0:15)))'; cfg = cfgAP{ap}; % For DL end % Set different channel for UL and DL, assuming that the channel is not reciprocal reset(chan) % Generate HE Ranging NDP transmission tx = heRangingWaveformGenerator(cfg); % Introduce time delay (fractional and integer) in the transmit waveform txDelay = heDelaySignal(tx,sampleDelay(ap)); % Pad signal and pass through multipath channel txMultipath = chan([txDelay;zeros(50,cfg.NumTransmitAntennas)]); % Pass waveform through AWGN channel rx = awgn(txMultipath,snrVal); % Perform synchronization and channel estimation [chanEstActiveSC,integerOffset] = heRangingSynchronize(rx,cfg); % Estimate the transmission time between UL and DL if ~isempty(chanEstActiveSC) % If packet detection is successful % Estimate fractional delay with MUSIC super-resolution fracDelay = heRangingTOAEstimate(chanEstActiveSC,ofdmInfo.ActiveFFTIndices, ... ofdmInfo.FFTLength,sampleRate,numPaths); integerOffset = integerOffset - chDelay; % Account for channel filter delay intDelay = integerOffset/sampleRate; % Estimate integer time delay txTime(l) = intDelay + fracDelay; % Transmission time else % If packet detection fails txTime(l) = NaN; end end if ~any(isnan(txTime)) % If packet detection succeeds % TOA of UL waveform (t2) toaUL = todUL + txTime(1); % Time of departure of DL waveform (t3) todDL = toaUL + delayULDL; % TOA DL waveform (t4) toaDL = todDL + txTime(2); % Compute the RTT rtt = (toaDL-todUL) - (todDL-toaUL); % Estimate the distance between the STA and AP distEst(ap,iter,isnr) = (rtt/2)*speedOfLight; % Accumulate error to MAE rangingError = rangingError + abs(distanceAllAPs(ap) - distEst(ap,iter,isnr)); else % If packet detection fails distEst(ap,iter,isnr) = NaN; failedPackets = failedPackets + 1; end end end mae = rangingError/((numAPs*numIterations) - failedPackets); % MAE for successful packets per(isnr) = failedPackets/(numAPs*numIterations); % PER if(per(isnr) > 0.01) % Use only successful packets for ranging and positioning warning('wlan:discardPacket','At SNR = %d dB, %d%% of packets were discarded',snrRange(isnr),100*per(isnr)); end disp(['At SNR = ',num2str(snrRange(isnr)),' dB, ','Ranging mean absolute error = ',num2str(mae), ' meters.']) end
At SNR = 15 dB, Ranging mean absolute error = 0.66554 meters. At SNR = 25 dB, Ranging mean absolute error = 0.51655 meters. At SNR = 35 dB, Ranging mean absolute error = 0.30264 meters.
% Reshape to consider all packets within one SNR point as one dataset rangingError = reshape(abs(distance - distEst),[numAPs*numIterations,numSNR]); hePlotErrorCDF(rangingError,snrRange) xlabel('Absolute ranging error (meters)') title('Ranging Error CDF')

Trilateration
Trilaterate the location of the STA in two dimensions by using the distance estimates, then calculate the positioning root-mean-square error (RMSE) for each iteration by using the STA position estimate. Display the average RMSE and its CDF for each SNR point.
positionSTAEst = zeros(2,numIterations,numSNR); RMSE = zeros(numIterations,numSNR); for isnr = 1:numSNR for i = 1:numIterations positionSTAEst(:,i,isnr) = hePositionEstimate(squeeze(positionAP(:,:,i,isnr)),squeeze(distEst(:,i,isnr))); end % Find the RMSE for each iteration, then take the mean of all RMSEs RMSE = reshape(sqrt(mean(((positionSTAEst-positionSTA).^2),1)),[numIterations numSNR]); posEr = mean(RMSE(:,isnr),'all','omitnan'); disp(['At SNR = ',num2str(snrRange(isnr)),' dB, ', 'Average RMS Positioning error = ', num2str(posEr), ' meters.']) end
At SNR = 15 dB, Average RMS Positioning error = 0.7014 meters. At SNR = 25 dB, Average RMS Positioning error = 0.52933 meters. At SNR = 35 dB, Average RMS Positioning error = 0.30314 meters.
hePlotErrorCDF(RMSE,snrRange) xlabel('RMS positioning error (meters)') title('Positioning Error CDF')

Plot the location estimate and the trilateration circles of the last iteration.
hePlotTrilaterationCircles(positionAP(:,:,numIterations,numSNR),positionSTAEst(:,numIterations,numSNR),distEst(:,numIterations,numSNR),snrRange(numSNR),numIterations);
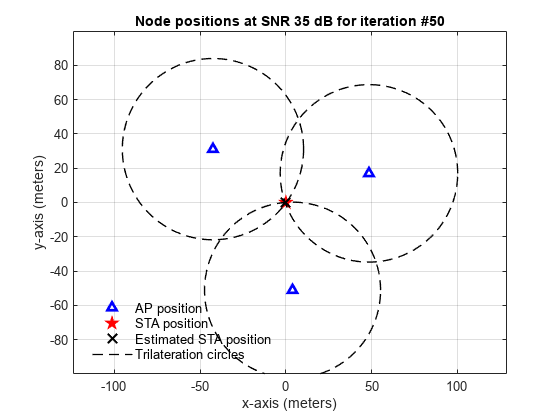
Conclusion
This example shows how to use a positioning algorithm with the IEEE® 802.11az™ standard. In particular, the example shows how to estimate the transmit-receive distance between a STA and AP by using MUSIC super-resolution, and how to locate a STA in two dimensions by using the ranging measurements from multiple STA-AP pairs. The example demonstrates the increase in performance of the positioning system at higher SNRs by computing the positioning estimate at multiple SNR points.
Further Exploration
Besides SNR, several important parameters impact positioning performance, such as HE-LTF repetitions, number of spatial streams, higher bandwidths, and channel delay profiles. This figure shows the impact of HE-LTF repetitions on ranging performance. To generate this figure, run a longer simulation with three randomly placed APs and 4000 iterations for a Model-B 22 MIMO channel of 20 MHz at 20 dB SNR. The figure shows that the ranging error decreases with the increase in HE-LTF repetitions. This decrease occurs because HE-LTF repetitions effectively reduce the noise in the CFR by averaging out multiple CFR estimates.

This figure shows the impact of different MIMO configurations on ranging performance. To generate this figure, run a longer simulation with three randomly placed APs and 4000 iterations, generating ranging packets with three HE-LTF repetitions at 20 MHz and specifying a Model-B channel at 20 dB SNR. The figure shows that the ranging error decreases with higher-order MIMO configurations. This decrease occurs because higher-order MIMO configurations produce more CFR snapshots from the different spatial streams available. More CFR snapshots give a better correlation matrix estimate which yields better ToA and distance estimates.

Related Examples
Three-Dimensional Indoor Positioning with 802.11az Fingerprinting and Deep Learning. Trains a convolutional neural network (CNN) for localization and positioning by using Deep Learning Toolbox and IEEE 802.11az data generated with WLAN Toolbox.
802.11az Waveform Generation. Parameterizes and generates IEEE 802.11az high-efficiency (HE) ranging null data packet (NDP) waveforms and highlights some of the key features of the standard.
References
IEEE Std 802.11az™-2022. IEEE Standard for Information technology— Telecommunications and information exchange between systems Local and metropolitan area networks— Specific requirements - Amendment 3: Enhancements for positioning.
IEEE Std 802.11ax™-2021. IEEE Standard for Information Technology - Telecommunications and Information Exchange between Systems - Local and Metropolitan Area Networks - Specific Requirements - Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications - Amendment 1: Enhancements for High Efficiency WLAN.
Xinrong Li and K. Pahlavan, "Super-resolution TOA estimation with diversity for indoor geolocation," in IEEE Transactions on Wireless Communications, vol. 3, no. 1, pp. 224-234, Jan. 2004, doi: 10.1109/TWC.2003.819035.