wtmm
Wavelet transform modulus maxima
Syntax
Description
[___] = wtmm(
uses only scales greater than or equal to x,MinRegressionScale=scale)scale to estimate
the global Hölder exponent. This syntax can include any of the output arguments
used in previous syntaxes.
[
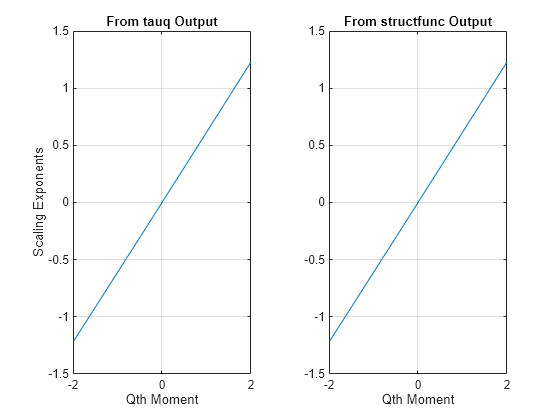
also returns the multiresolution structure functions,
hexp,tauq,structfunc] = wtmm(___)structfunc, for the global Hölder exponent estimate.
This syntax can include any of the input arguments used in previous
syntaxes.
[
returns the local Hölder exponent estimates localhexp,wt,wavscales] = wtmm(x,ScalingExponent="local")localhexp, the
continuous wavelet transform (CWT) of the signal, wt, and
the scales wavscales used in the CWT.
wtmm(___, with
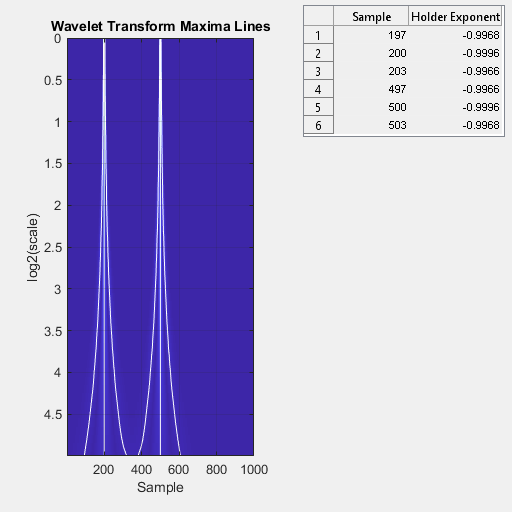
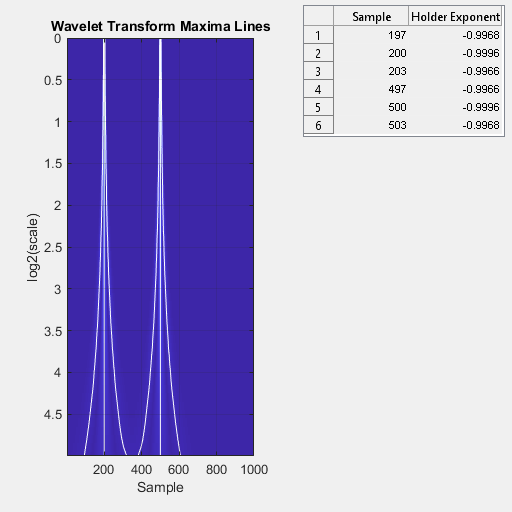
no output arguments plots the wavelet maxima lines in the current figure.
Estimates of the local Hölder exponents are displayed in a table to the right of
the plot.ScalingExponent="local")
[___] = wtmm(___,
returns the Hölder exponent and other specified outputs with additional options
specified by one or more Name=Value)Name=Value arguments.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Algorithms
The WTMM algorithm finds singularities in a signal by determining maxima. The WTMM is intended to be used with large data sets so that enough samples are available to determine maxima accurately.
An overview of the algorithm follows.
The algorithm calculates the continuous wavelet transform (CWT) using the second derivative of the Gaussian wavelet with 10 voices per octave. The Ricker wavelet meets this criteria.
At the initial scale, the algorithm determines the modulus maxima.
The algorithm continues up through finer scales, finding the modulus maxima and checking whether the maxima align between scales. If a maximum converges to the finest scale, it is a true maximum and indicates a singularity at that point.
When each singularity is determined, the algorithm estimates its Hölder exponent.
For signals with a few cusp-like singularities and Hölder exponents that have large variation, you set the algorithm to return local Hölder exponents, which provide individual values for each singularity. For signals with numerous Hölder exponents that have relatively small variations, you set the algorithm to return a global Hölder exponent. A global Hölder exponent applies to the whole signal. For signals with many singularities, you can reduce the number of maxima found by limiting the algorithm to start at or regress to a specific minimum or maximum scale, respectively. For detailed information about the WTMM, see [1] and [3].
References
[1] Mallat, S., and W.L. Hwang. “Singularity Detection and Processing with Wavelets.” IEEE Transactions on Information Theory 38, no. 2 (March 1992): 617–43. https://doi.org/10.1109/18.119727.
[2] Wendt, Herwig, and Patrice Abry. “Multifractality Tests Using Bootstrapped Wavelet Leaders.” IEEE Transactions on Signal Processing 55, no. 10 (October 2007): 4811–20. https://doi.org/10.1109/TSP.2007.896269.
[3] Arneodo, Alain, Benjamin Audit, Nicolas Decoster, Jean-Francois Muzy, and Cedric Vaillant. “Wavelet Based Multifractal Formalism: Applications to DNA Sequences, Satellite Images of the Cloud Structure, and Stock Market Data.” In The Science of Disasters, by Armin Bunde, Jürgen Kropp, and Hans Joachim Schellnhuber, 26–102. Berlin, Heidelberg: Springer Berlin Heidelberg, 2002. https://doi.org/10.1007/978-3-642-56257-0_2.
Version History
Introduced in R2016b