wentropy
Wavelet entropy
Description
Examples
Shannon Entropy
Create a signal whose samples are alternating values of 0 and 2.
n = 0:499; x = 1+(-1).^n; stem(x) axis tight title("Signal") xlim([0 50])
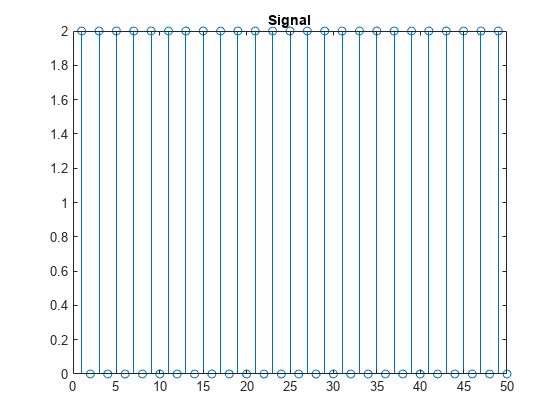
Obtain the scaled Shannon entropy of the signal. Specify a one-level wavelet transform, use the default wavelet and wavelet transform.
ent = wentropy(x,Level=1); ent
ent = 2×1
1.0000
1.0000
Obtain the unscaled Shannon entropy. Divide the entropy by log(n), where n is the length of the signal. Confirm the result equals the scaled entropy.
ent2 = wentropy(x,Level=1,Scaled=false); ent2/log(length(x))
ans = 2×1
1.0000
1.0000
Create a zero-mean signal from the first signal. Obtain the scaled Shannon entropy of the new signal using a one-level wavelet transform.
x = x-1; ent = wentropy(x,Level=1); ent
ent = 2×1
1.0000
0
Renyi Entropy
Load the Kobe earthquake data. Obtain the level 4 tunable Q-factor wavelet transform of the data with a quality factor equal to 2.
load kobe
wt = tqwt(kobe,Level=4,QualityFactor=2);Obtain the Renyi entropy estimates for the tunable Q-factor transform.
ent = wentropy(wt,Entropy="Renyi");
entent = 5×1
0.8288
0.8506
0.8582
0.8536
0.7300
Load the ECG data. Obtain the level 5 discrete wavelet transform of the signal using the "db4" wavelet.
load wecg wv = "db4"; [C,L] = wavedec(wecg,5,wv);
Package the wavelet and approximation coefficients into a cell array suitable for computing the wavelet entropy.
X = detcoef(C,L,"cells");
X{end+1} = appcoef(C,L,wv);Obtain the Renyi entropy by scale.
ent = wentropy(X,Entropy="Renyi");
entent = 6×1
0.2412
0.5239
0.5459
0.6520
0.7661
0.8547
Tsallis Entropy
Create a Kronecker delta sequence.
N = 512; seq = zeros(1,N); seq(N/2) = 1;
Obtain the scaled Shannon entropy of the signal. Specify a level 3 wavelet transform.
ShannonEntropy = wentropy(seq,Level=3);
Obtain the scaled Tsallis entropy of the signal for different values of exponents. Confirm that as the exponent goes to 1, the Tsallis entropy approaches the Shannon entropy.
exps = 3:-1/4:1; TsallisExponent = zeros(length(exps),1); TsallisEntropy = zeros(length(exps),4); ctr = 1; for k=exps ent2 = wentropy(seq,Level=3,Entropy="Tsallis",Exponent=k); TsallisExponent(ctr) = k; TsallisEntropy(ctr,:) = ent2'; ctr = ctr+1; end TsallisTable = table(TsallisExponent,TsallisEntropy)
TsallisTable=9×2 table
TsallisExponent TsallisEntropy
_______________ ________________________________________
3 0.71454 0.87888 0.97069 0.98285
2.75 0.67651 0.84955 0.95685 0.97233
2.5 0.63178 0.81187 0.93596 0.9552
2.25 0.57852 0.7628 0.90407 0.92718
2 0.51437 0.69812 0.85499 0.88149
1.75 0.43679 0.61258 0.77985 0.80825
1.5 0.34491 0.50213 0.66897 0.69658
1.25 0.24402 0.37071 0.52076 0.54417
1 0.1495 0.23839 0.356 0.37278
ShannonEntropy'
ans = 1×4
0.1495 0.2384 0.3560 0.3728
Input Arguments
Input data, specified as a real-valued row or column vector, a cell array of real-valued row or column vectors, or a real-valued matrix with at least two rows.
If
Xis a row or column vector,Xmust have at least four samples, and the function assumesXrepresents time data.If
Xis a cell array, the function assumesXto be a decimated wavelet or wavelet packet transform of a real-valued row or column vector.If
Xis a matrix with at least two rows, the function assumesXto be the maximal overlap discrete wavelet or wavelet packet transform of a real-valued row or column vector.
Example: ent = wentropy(randn(1,1024)) returns the
normalized Shannon wavelet entropy. wentropy computes
the wavelet coefficients using the default options of
modwt.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: ent = wentropy(X,Wavelet="coif4") uses the
"coif4" wavelet to obtain the wavelet
transform.
Entropy returned by wentropy, specified as one of
"Shannon", "Renyi", and
"Tsallis". For more information, see Wavelet Entropy.
Exponent to use in the Renyi and Tsallis entropy, specified as a real scalar.
For the Renyi entropy, the exponent must be nonnegative.
For the Tsallis entropy, the exponent must be greater than or equal to
–1/2.For the Renyi and Tsallis entropies, specifying
Exponent=1
Specifying Exponent is valid only
when Entropy is "Renyi" or
"Tsallis". For more information, see Wavelet Entropy.
Note
When you specify a negative exponent for the Tsallis entropy, entropy computations may become unstable with small changes in the wavelet coefficient energies, resulting in significant changes in the entropy values.
Data Types: single | double
Transform to use to obtain the wavelet or wavelet packet coefficients, specified as one of these:
"dwt"— Discrete wavelet transform"dwpt"— Discrete wavelet packet transform"modwt"— Maximal overlap discrete wavelet transform"modwpt"— Maximal overlap discrete wavelet packet transform
Periodic extension is used for all transforms.
Specifying a transform is invalid if the input data are wavelet or wavelet packet coefficients.
Wavelet decomposition level if the input X is
time data, specified as a positive integer. The
wentropy function obtains the wavelet transform
down to the specified level. If unspecified, the default level depends
on the type of transform and the signal length N.
If
Transformis"dwt"or"modwt",Leveldefaults tofloor(log2(N))-1.If
Transformis"dwpt"or"modwpt",Leveldefaults tomin(4,floor(log2(N))-1).
Specifying a level is invalid if the input data are wavelet or wavelet packet coefficients.
Data Types: single | double
Wavelet to use in the transform, specified as a character vector or
string scalar. If Transform is
"modwt" or "modwpt", the
wavelet must be orthogonal. The default wavelet depends on the value of
Transform.
If
Transformis"dwt"or"modwt",wentropyuses the"sym4"wavelet.If
Transformis"dwpt"or"modwpt",wentropyuses the"fk18"wavelet.
For a list of supported orthogonal and biorthogonal
wavelets, see wfilters.
Specifying a wavelet name is invalid if the input data are wavelet or wavelet packet coefficients.
Data Types: char | string
Normalization method to use to obtain the empirical probability
distribution for the wavelet transform coefficients, specified as
"scale" or "global".
"global"— The function normalizes the squared magnitudes of the coefficients by the total sum of squared magnitudes of all coefficients. Each scale in the wavelet transform yields a scalar and the vector of these values forms a probability vector. The function performs entropy calculations on this vector and the overall entropy is a scalar."scale"— The function normalizes the wavelet coefficients at each scale separately and calculates the entropy by scale.If the input is time series data, the output
entis of size (Ns+1)-by-1, where Ns is the number of scales.If the input is a cell array or matrix,
entis of size M-by-1, where M is the length of the cell array or number of rows in the matrix.
For more information, see Wavelet Entropy.
Scale wavelet entropy logical, specified as a numeric or logical
1 (true) or
0 (false). If specified as
true, the wentropy function
scales the wavelet entropy by the factor corresponding to a uniform
distribution for the specified entropy.
For the Shannon and Renyi entropies, the factor is
1/log(Nj), where Nj is the length of the data in samples by scale ifDistributionis"scale", or the number of scales ifDistributionis"global".For the Tsallis entropy, the factor is
(.Exponent-1)/(1-Nj^(1-Exponent))
Setting
Scaled=false
Data Types: logical
Energy threshold, specified as a nonnegative scalar. The function
replaces all coefficients with energy by scale below
EnergyThreshold with 0. A positive
EnergyThreshold prevents the function from
treating wavelet or wavelet packet coefficients with nonsignificant
energy as a sequence with high entropy.
Data Types: single | double
Output Arguments
Entropy of X, returned as a scalar or vector.
If
Xis time data,entis a real-valued (Ns+1)-by-1 vector of entropy estimates by scale, where Ns is the number of scales.If
Xis a wavelet or wavelet packet transform input,entis a real-valued column vector with length equal to the length ofXifXis a cell array or the row dimension ofXifXis a matrix.
See Distribution to obtain global
estimates of the wavelet entropy. The wentropy function
uses the natural logarithm to compute the entropy.
Data Types: single | double
Relative wavelet energy, returned as a vector or matrix.
If
Distribution="scale"If
Distribution="global"
Scales where the coefficient energy is below the value of
EnergyThreshold are equal to 0.
Data Types: single | double
More About
Wavelet entropy (WE) is often used to analyze nonstationary signals. WE combines a wavelet or wavelet decomposition with a measure of order within the wavelet coefficients by scale. These measures of order are referred to as entropy measures. WE treats the normalized wavelet coefficients as an empirical probability distribution and calculates its entropy.
You can normalize the wavelet coefficients in one of two ways.
The function normalizes all the coefficients by the total sum of their squared magnitudes: where j corresponds to time, and i corresponds to scale. The probability mass function is: To use this normalization, set
Distributionto"global".The function normalizes the coefficients at each scale separately by the sum of their squared magnitudes: The probability mass function is: To use this normalization, set
Distributionto"scale".
The wentropy function supports three entropy measures.
Shannon Entropy
For a discrete random variable
X, the Shannon entropy is defined as:where the sum is taken over all values that the random variable can take. By convention, 0 ln(0) = 0.
Renyi Entropy
The Renyi entropy is defined as:
In the limit, the Renyi entropy becomes the Shannon entropy:
Tsallis Entropy
The Tsallis entropy is defined as:
Similar to the Renyi entropy, in the limit, the Tsallis entropy becomes the Shannon entropy:
References
[1] Zunino, L., D.G. Pérez, M. Garavaglia, and O.A. Rosso. “Wavelet Entropy of Stochastic Processes.” Physica A: Statistical Mechanics and Its Applications 379, no. 2 (June 2007): 503–12. https://doi.org/10.1016/j.physa.2006.12.057.
[2] Rosso, Osvaldo A., Susana Blanco, Juliana Yordanova, Vasil Kolev, Alejandra Figliola, Martin Schürmann, and Erol Başar. “Wavelet Entropy: A New Tool for Analysis of Short Duration Brain Electrical Signals.” Journal of Neuroscience Methods 105, no. 1 (January 2001): 65–75. https://doi.org/10.1016/S0165-0270(00)00356-3.
[3] Alcaraz, Raúl, ed. "Wavelet Entropy: Computation and Applications." Special issue, Entropy 17 (2015). https://www.mdpi.com/journal/entropy/special_issues/wavelet-entropy.
Extended Capabilities
Usage notes and limitations:
The values of the
Wavelet,Transform, andDistributionname-value arguments must be constant at compile time. Usecoder.Constant(MATLAB Coder).Vector inputs must have one dimension fixed at 1 at compile time. For example, to allow for row vector input with unbounded size, specify the first input argument at compile time as
{coder.typeof(0,[1 Inf],[0 1]])}. For more information, seecoder.typeof(MATLAB Coder).When you compile with variable-size dimensions for both row and column input, the generated code expects matrix input. For example, if you specify the first input argument at compile time as
{coder.typeof(0,[1 Inf],[1 1])}, the generated code errors for row vector input.The syntax used in the old version of the
wentropyfunction is not supported. For more information, see Version History.
The wentropy function
supports GPU array input with these usage notes and limitations:
The
"dwpt"transform is not supported.The syntax used in the old version of the
wentropyfunction is not supported. For more information, see Version History
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced before R2006aThe wentropy function supports:
C/C++ code generation. You must have MATLAB® Coder™ to generate C/C++ code.
gpuArrayobject inputs. You must have Parallel Computing Toolbox™ to usegpuArrayobjects.
The syntax used in the old version of wentropy continues to
work, but is no longer recommended. The old version provides you minimal control
over how to estimate the entropy. The wentropy function
automatically determines from the input syntax which version to use.
You can specify the Shannon entropy in both versions of
wentropy. However, because the old version makes no
assumptions about the input data, reproducing the same results as the new version
can require extensive effort.
| Old Version | New Version |
|---|---|
load wecg n = numel(wecg); lev = 3; wt = modwt(wecg,lev); energy = sum(abs(wt).^2,2); wt2 = abs(wt)./sqrt(energy); ent = zeros(lev+1,1); for k=1:lev+1 ent(k) = wentropy(wt2(k,:),'shannon')/log(n); end ent ent =
0.3925
0.6512
0.6985
0.9329 |
load wecg
ent = wentropy(wecg,Level=3)
ent =
0.3925
0.6512
0.6985
0.9329 |
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)