symaux
Symlet wavelet filter computation
Description
The symaux function generates the scaling filter coefficients
for the "least asymmetric" Daubechies wavelets.
w = symaux(n)n Symlet scaling filter such that sum(w) =
1.
Note
Instability may occur when
nis too large. Starting with values ofnin the 30s range, function output will no longer accurately represent scaling filter coefficients.As
nincreases, the time required to compute the filter coefficients rapidly grows.For
n= 1, 2, and 3, the ordernSymlet filters and ordernDaubechies filters are identical. See Extremal Phase Wavelet.
Examples
In this example you will generate symlet scaling filter coefficients whose norm is equal to 1. You will also confirm the coefficients satisfy a necessary relation.
Compute the scaling filter coefficients of the order 10 symlet whose sum equals.
n = 10; w = symaux(n,sqrt(2));
Confirm the sum of the coefficients is equal to and the norm is equal to 1.
sqrt(2)-sum(w)
ans = 2.2204e-16
1-sum(w.^2)
ans = -3.3307e-14
Since integer translations of the scaling function form an orthogonal basis, the coefficients satisfy the relation . Confirm this by taking the autocorrelation of the coefficients and plotting the result.
corrw = xcorr(w,w); stem(corrw) grid on title('Autocorrelation of scaling coefficients')
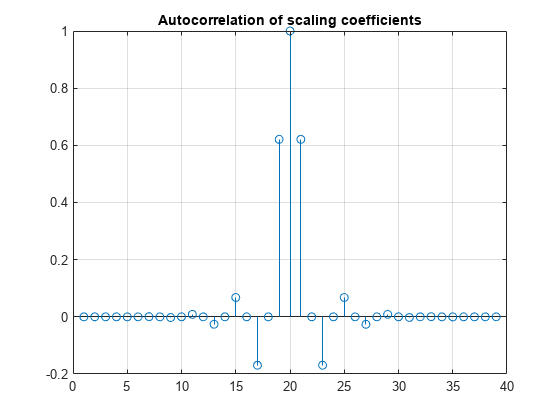
stem(corrw(2:2:end)) grid on title('Even-indexed autocorrelation values')

This example shows that symlet and Daubechies scaling filters of the same order are both solutions of the same polynomial equation.
Generate the order 4 Daubechies scaling filter and plot it.
wdb4 = dbaux(4);
stem(wdb4)
title('Order 4 Daubechies Scaling Filter')
wdb4 is a solution of the equation: P = conv(wrev(w),w)*2, where P is the "Lagrange trous" filter for N = 4. Evaluate P and plot it. P is a symmetric filter and wdb4 is a minimum phase solution of the previous equation based on the roots of P.
P = conv(wrev(wdb4),wdb4)*2;
stem(P)
title('''Lagrange trous'' filter')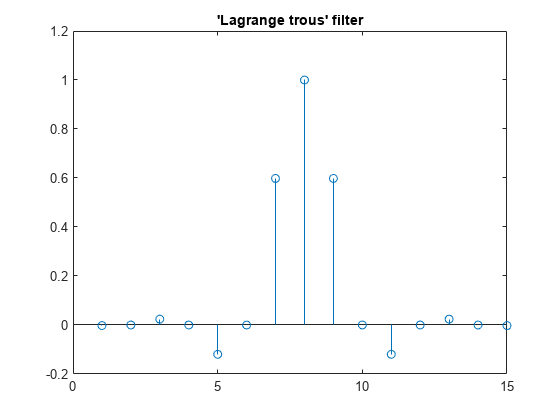
Generate wsym4, the order 4 symlet scaling filter and plot it. The Symlets are the "least asymmetric" Daubechies' wavelets obtained from another choice between the roots of P.
wsym4 = symaux(4);
stem(wsym4)
title('Order 4 Symlet Scaling Filter')
Compute conv(wrev(wsym4),wsym4)*2 and confirm that wsym4 is another solution of the equation P = conv(wrev(w),w)*2.
P_sym = conv(wrev(wsym4),wsym4)*2; err = norm(P_sym-P)
err = 1.2491e-15
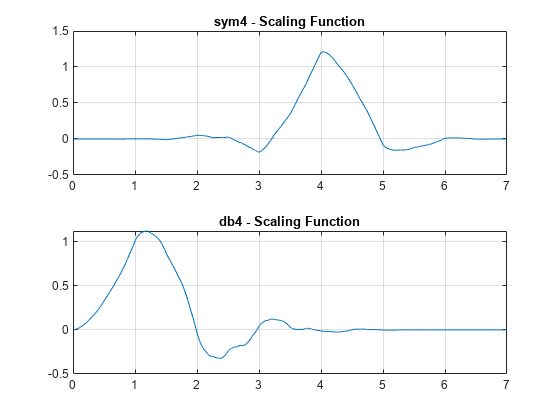
For a given support, the orthogonal wavelet with a phase response that most closely resembles a linear phase filter is called least asymmetric. Symlets are examples of least asymmetric wavelets. They are modified versions of the classic Daubechies db wavelets. In this example, you will show that the order 4 symlet has a nearly linear phase response, while the order 4 Daubechies wavelet does not.
First plot the order 4 symlet and order 4 Daubechies scaling functions. While neither is perfectly symmetric, note how much more symmetric the symlet is.
[phi_sym,~,xval_sym]=wavefun('sym4',10); [phi_db,~,xval_db]=wavefun('db4',10); subplot(2,1,1) plot(xval_sym,phi_sym) title('sym4 - Scaling Function') grid on subplot(2,1,2) plot(xval_db,phi_db) title('db4 - Scaling Function') grid on
Generate the filters associated with the order 4 symlet and Daubechies wavelets.
scal_sym = symaux(4,sqrt(2)); scal_db = dbaux(4,sqrt(2));
Compute the frequency response of the scaling synthesis filters.
[h_sym,w_sym] = freqz(scal_sym); [h_db,w_db] = freqz(scal_db);
To avoid visual discontinuities, unwrap the phase angles of the frequency responses and plot them. Note how well the phase angle of the symlet filter approximates a straight line.
h_sym_u = unwrap(angle(h_sym)); h_db_u = unwrap(angle(h_db)); figure plot(w_sym/pi,h_sym_u,'.') hold on plot(w_sym([1 end])/pi,h_sym_u([1 end]),'r') hold off grid on xlabel('Normalized Frequency ( x \pi rad/sample)') ylabel('Phase (radians)') legend('Phase Angle of Frequency Response','Straight Line') title('Symlet Order 4 - Phase Angle')
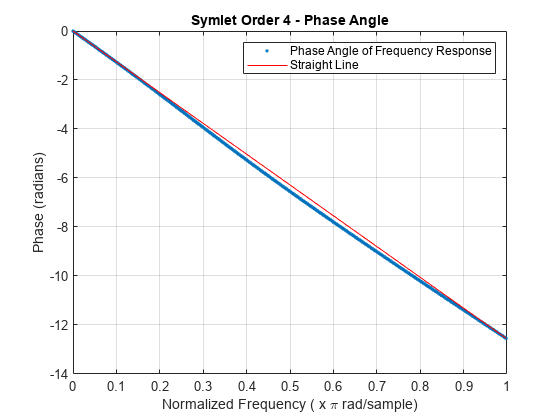
figure plot(w_db/pi,h_db_u,'.') hold on plot(w_db([1 end])/pi,h_db_u([1 end]),'r') hold off grid on xlabel('Normalized Frequency ( x \pi rad/sample)') ylabel('Phase (radians)') legend('Phase Angle of Frequency Response','Straight Line') title('Daubechies Order 4 - Phase Angle')

The sym4 and db4 wavelets are not symmetric, but the biorthogonal wavelet is. Plot the scaling function associated with the bior3.5 wavelet. Compute the frequency response of the synthesis scaling filter for the wavelet and verify that it has linear phase.
[~,~,phi_bior_r,~,xval_bior]=wavefun('bior3.5',10); figure plot(xval_bior,phi_bior_r) title('bior3.5 - Scaling Function') grid on
[LoD_bior,HiD_bior,LoR_bior,HiR_bior] = wfilters('bior3.5'); [h_bior,w_bior] = freqz(LoR_bior); h_bior_u = unwrap(angle(h_bior)); figure plot(w_bior/pi,h_bior_u,'.') hold on plot(w_bior([1 end])/pi,h_bior_u([1 end]),'r') hold off grid on xlabel('Normalized Frequency ( x \pi rad/sample)') ylabel('Phase (radians)') legend('Phase Angle of Frequency Response','Straight Line') title('Biorthogonal 3.5 - Phase Angle')

This example demonstrates that for a given support, the cumulative sum of the squared coefficients of a scaling filter increase more rapidly for an extremal phase wavelet than other wavelets.
Generate the scaling filter coefficients for the db15 and sym15 wavelets. Both wavelets have support of width .
[~,~,LoR_db,~] = wfilters('db15'); [~,~,LoR_sym,~] = wfilters('sym15');
Next, generate the scaling filter coefficients for the coif5 wavelet. This wavelet also has support of width .
[~,~,LoR_coif,~] = wfilters('coif5');Confirm the sum of the coefficients for all three wavelets equals .
sqrt(2)-sum(LoR_db)
ans = 4.4409e-16
sqrt(2)-sum(LoR_sym)
ans = -2.2204e-16
sqrt(2)-sum(LoR_coif)
ans = 2.2204e-16
Plot the cumulative sums of the squared coefficients. Note how rapidly the Daubechies sum increases. This is because its energy is concentrated at small abscissas. Since the Daubechies wavelet has extremal phase, the cumulative sum of its squared coefficients increases more rapidly than the other two wavelets.
plot(cumsum(LoR_db.^2),'rx-') hold on plot(cumsum(LoR_sym.^2),'mo-') plot(cumsum(LoR_coif.^2),'b*-') hold off legend('Daubechies','Symlet','Coiflet') title('Cumulative Sum')

Input Arguments
Order of the symlet, specified as a positive integer.
Sum of the scaling filter coefficients, specified as a positive real number. Set to
sqrt(2) to generate vector of coefficients whose norm is 1.
Output Arguments
Vector of scaling filter coefficients of the order n
symlet.
The scaling filter coefficients satisfy a number of properties. You can use these properties to check your results. See Unit Norm Scaling Filter Coefficients for additional information.
More About
The Haar wavelet, also known as the Daubechies wavelet of order 1,
db1, is the only compactly supported orthogonal wavelet that is
symmetric, or equivalently has linear phase. No other compactly supported orthogonal wavelet
can be symmetric. However, it is possible to derive wavelets which are minimally asymmetric,
meaning that their phase will be very nearly linear. For a given support, the orthogonal
wavelet with a phase response that most closely resembles a linear phase filter is called
least asymmetric.
Constructing a compactly supported orthogonal wavelet basis involves choosing roots of a particular polynomial equation. Different choices of roots will result in wavelets whose phases are different. Choosing roots that lie within the unit circle in the complex plane results in a filter with highly nonlinear phase. Such a wavelet is said to have extremal phase, and has energy concentrated at small abscissas. Let {hk} denote the set of scaling coefficients associated with an extremal phase wavelet, where k = 1,…,M. Then for any other set of scaling coefficients {gk} resulting from a different choice of roots, the following inequality holds for all J = 1,…,M:
The {hk} are sometimes called a minimal delay filter [2].
The polynomial equation mentioned above depends on the desired number of vanishing
moments N for the wavelet. To construct a wavelet basis involves
choosing roots of the equation. In the case of least asymmetric wavelets and extremal phase
wavelets for orders 1, 2, and 3, there are effectively no choices to make. For
N = 1, 2, and 3, the dbN and
symN filters are equal. The example Symlet and Daubechies Scaling Filters shows that two
different scaling filters can satisfy the same polynomial equation. For additional
information, see Daubechies [1].
References
[1] Daubechies, I. Ten Lectures on Wavelets, CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA: SIAM Ed, 1992.
[2] Oppenheim, Alan V., and Ronald W. Schafer. Discrete-Time Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1989.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)