iwsst

Inverse wavelet synchrosqueezed transform

Syntax

xrec = iwsst(sst)

xrec = iwsst(sst,f,freqrange)

xrec = iwsst(sst,iridge)

xrec = iwsst(___,wav)

xrec = iwsst(___,iridge,'NumFrequencyBins',numBins)

Description

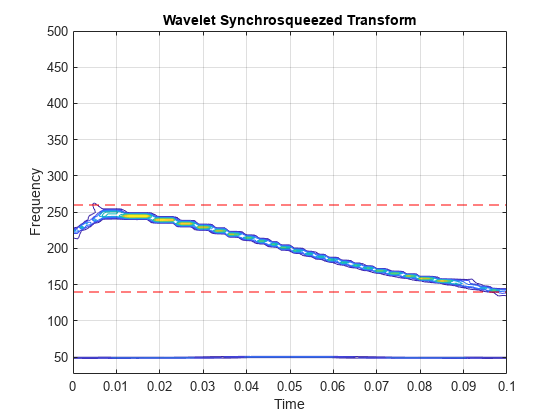
xrec = iwsst(sst) inverts the input synchrosqueezed transform, sst, and returns the inverse in vector xrec. To obtain the sst input, use the wsst function. The iwsst function assumes that you obtain sst using the analytic Morlet wavelet.

Note

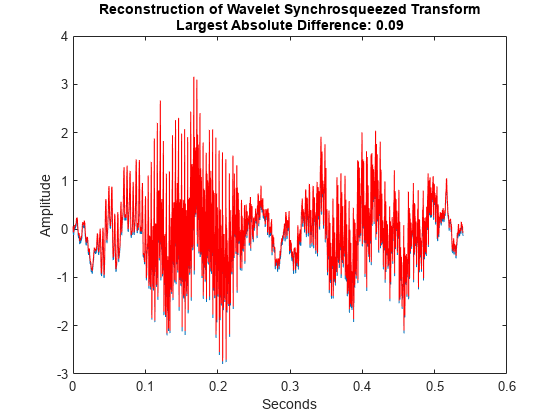
The wavelet transform does not preserve a nonzero mean. After inverting the synchrosqueezed transform, you must add back the original signal mean.

xrec = iwsst(sst,f,freqrange) inverts the synchrosqueezed transform for a specified range of frequencies, freqrange, contained in the frequency vector, f. The frequency vector, f, is the output of wsst.

xrec = iwsst(sst,iridge) inverts the synchrosqueezed transform along the time-frequency ridges specified by iridge, the index column vector. iridge is the output of wsstridge. The xrec output is the same size as iridge.

xrec = iwsst(___,wav) uses the analytic wavelet specified by wav to invert the synchrosqueezed transform. This wavelet must be the same wavelet as used in wsst. You can include any of the input arguments from previous syntaxes.

xrec = iwsst(___,iridge,'NumFrequencyBins',numBins) returns the inverse synchrosqueezed transform with numBins-many additional frequency bins included on either side of each iridge index bin.

Examples

Inverse Synchrosqueezed Transform of Chirp

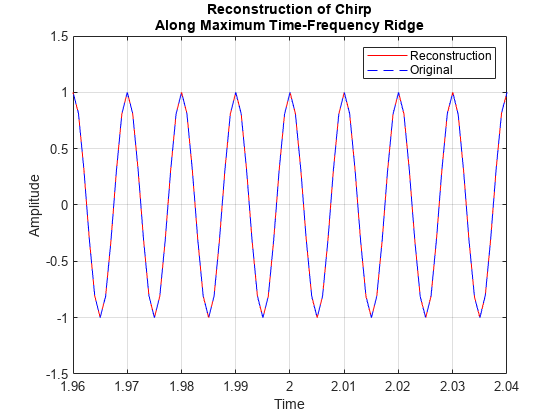
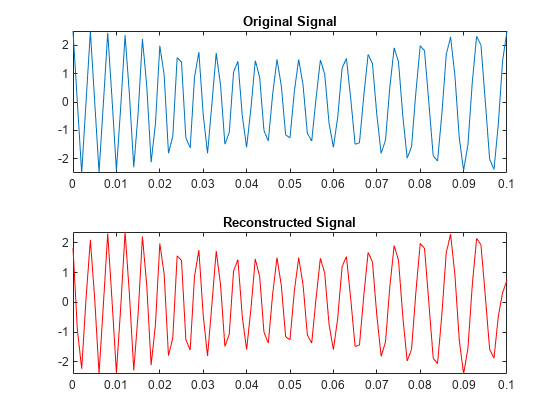
Obtain the wavelet synchrosqueezed transform of a quadratic chirp using default values. Then reconstruct the signal using the inverse wavelet synchrosqueezed transform.

load quadchirp;
sst = wsst(quadchirp);
xrec = iwsst(sst);

Synchrosqueezed and Inverse Synchrosqueezed Transform of Chirp

Obtain the wavelet synchrosqueezed transform of a quadratic chirp sampled at 1000 Hz. Then reconstruct the chirp.

Load the chirp and obtain the synchrosqueezed transform.

load quadchirp;
sstchirp = wsst(quadchirp,'ExtendSignal',true);

Extract the maximum energy time-frequency ridge and reconstruct the signal mode along the ridge.

[~,iridge] = wsstridge(sstchirp);
xrec = iwsst(sstchirp,iridge);

Plot and zoom in on the original and reconstructed signal.

plot(tquad,xrec,'r');
hold on;
plot(tquad,quadchirp,'b--');
xlabel('Time'); ylabel('Amplitude');
set(gca,'ylim',[-1.5 1.5]);
legend('Reconstruction','Original');
grid on;
title('Reconstruction of Chirp Along Maximum Time-Frequency Ridge');
zoom xon
zoom(50)

Inverse Synchrosqueezed Transform of Range of Frequencies

Obtain the inverse synchrosqueezed transform for a specified frequency range of a two-component signal. The input is a combination of an amplitude-modulated and a frequency-modulated signal.

Create the signal.

t = 0:0.001:0.1;
x1 = (2+0.5*cos(2*pi*10*t)).*cos(2*pi*200*t+10*sin(2*pi*5*t));
x2 = cos(2*pi*50*t);
sig = x1+x2;

Obtain the wavelet synchrosqueezed transform and plot the resulting two frequency components.

[sst,f] = wsst(sig,1000,'ExtendSignal',true);
contour(t,f,abs(sst));
grid on;
title('Wavelet Synchrosqueezed Transform');
ylabel('Frequency');
xlabel('Time');
hold on
plot(t,140*ones(size(t)),'r--');
plot(t,260*ones(size(t)),'r--');

Obtain the inverse synchrosqueezed transform for frequencies from 140 Hz to 260 Hz. Plot the result.

xrec = iwsst(sst,f,[140,260]);
subplot(2,1,1);
plot(t,x1);
title('Original Signal');
subplot(2,1,2);
plot(t,xrec,'r');
title('Reconstructed Signal');

Synchrosqueezed and Inverse Synchrosqueezed Transform of Speech Signal

Obtain the wavelet synchrosqueezed transform and inverse synchrosqueezed transform of a speech sample using the bump wavelet.

Load the speech signal and obtain the synchrosqueezed transform and inverse synchrosqueezed transform.

load mtlb
dt = 1/Fs;
t = 0:dt:numel(mtlb)*dt-dt;
Txmtlb = wsst(mtlb,'bump');
xrec = iwsst(Txmtlb,'bump');

Obtain the L-infinity norm of the difference between the original waveform and the reconstruction. Plot the results.

Linf = norm(abs(mtlb-xrec),Inf);
plot(t,mtlb)
hold on
xlabel('Seconds')
ylabel('Amplitude')
plot(t,xrec,'r')
title({'Reconstruction of Wavelet Synchrosqueezed Transform';...
    ['Largest Absolute Difference: ' num2str(Linf,'%1.2f')]})

Synchrosqueezed Transform Using Specified Number of Bins for Chirp

This example shows how to invert the wavelet synchrosqueezed transform using a specified number of frequency bins for a quadratic chirp. The chirp is sampled at 1000 Hz.

load quadchirp;
sstchirp = wsst(quadchirp,'ExtendSignal',true);

Extract the maximum energy time-frequency ridge using 10 bins on each side of the iridge index and reconstruct the signal mode along the ridge.

[~,iridge] = wsstridge(sstchirp);
xrec = iwsst(sstchirp,iridge,'NumFrequencyBins',10);

Plot the original and reconstructed signal.

plot(tquad,xrec,'r');
hold on;
plot(tquad,quadchirp,'b--');
xlabel('Time'); ylabel('Amplitude');
set(gca,'ylim',[-1.5 1.5]);
legend('Reconstruction','Original');
grid on;
title('Reconstruction of Chirp Along Maximum Time-Frequency Ridge');

Input Arguments

sst — Synchrosqueezed transform

matrix

Synchrosqueezed transform, specified as a matrix. sst is the output from the wsst function.

f — Synchrosqueezed transform frequencies

vector

Synchrosqueezed transform frequencies corresponding to the rows of the synchrosqueezed transform, specified as a vector. The number of elements in the frequency vector is equal to the number of rows in the sst input. If you specify f, you must also specify freqrange.

freqrange — Frequency range

two-element vector

Frequency range for which to return inverse synchrosqueezed transform values, specified as a two-element vector. The values of freqrange must be in the range of the values of the frequencies, f. The first and second elements of freqrange define the start and end of the frequency range, where the frequency values in that range must be positive and strictly increasing. If you specify freqrange, you must also specify f.

iridge — Time-frequency ridge row indices

vector or matrix

Time-frequency ridge row indices of the synchrosqueezed transform specified as a vector or matrix. iridge is the output of the wsstridge function. If iridge is a matrix, iwsst inverts the synchrosqueezed transform along the first column of iridge. Then, it iteratively reconstructs along subsequent columns of iridge. The sizes of iridge and the xrec output are the same.

wav — Analytic wavelet

'amor' (default) | 'bump'

Analytic wavelet used to compute the inverse synchrosqueezed transform, specified as one of the following:

• 'amor' — Analytic Morlet wavelet

• 'bump' — Bump wavelet

You must use the same wavelet in the reconstruction that you used to compute the synchrosqueezed transform, sst.

numBins — Number of additional frequency bins

16 (default) | positive integer

Number of additional frequency bins to include on either side of each iridge index bin, specified as a positive integer. If the number of additional bins exceeds the number of frequency bins available at a particular time step, iwsst truncates the reconstruction at the first or last frequency bin. The default, 16, is one half the default number of voices per octave.

To specify this argument, you also specify iridge, which is the output of wsstridge. You cannot include a frequency f and frequency range freqrange, if you include the number of frequency bins.

Output Arguments

xrec — Inverse synchrosqueezed transform

vector or matrix

Inverse synchrosqueezed transform, returned as a vector or matrix. If you do not specify an iridge input, xrec is a column vector with the same number of rows as sst. If you specify an iridge input, xrec is the same size as iridge.

References

[1] Daubechies, I., J. Lu, and H. T. Wu. "Synchrosqueezed Wavelet Transforms: an Empirical Mode Decomposition-like Tool." Applied and Computational Harmonic Analysis, Vol. 30, Number 2, 2011, pp. 243–261.

[2] Thakur, G., E. Brevdo, N. S. Fučkar, and H. T. Wu. "The Synchrosqueezing algorithm for time-varying spectral analysis: robustness properties and new paleoclimate applications." Signal Processing, Vol. 93, Number 5, 2013, pp. 1079–1094.

Version History

Introduced in R2016a