erfinv
Inverse error function
Syntax
Description
erfinv( computes the inverse error function of
X)X. If X is a vector or a matrix,
erfinv(X) computes the inverse error function of each element of
X.
Examples
Inverse Error Function for Floating-Point and Symbolic Numbers
Depending on its arguments, erfinv can return
floating-point or exact symbolic results.
Compute the inverse error function for these numbers. Because these numbers are not symbolic objects, you get floating-point results:
A = [erfinv(1/2), erfinv(0.33), erfinv(-1/3)]
A =
0.4769 0.3013 -0.3046Compute the inverse error function for the same numbers converted to symbolic objects.
For most symbolic (exact) numbers, erfinv returns unresolved symbolic
calls:
symA = [erfinv(sym(1)/2), erfinv(sym(0.33)), erfinv(sym(-1)/3)]
symA = [ erfinv(1/2), erfinv(33/100), -erfinv(1/3)]
Use vpa to approximate symbolic results with the required number of
digits:
d = digits(10); vpa(symA) digits(d)
ans = [ 0.4769362762, 0.3013321461, -0.3045701942]
Inverse Error Function for Variables and Expressions
For most symbolic variables and expressions,
erfinv returns unresolved symbolic calls.
Compute the inverse error function for x and sin(x) +
x*exp(x). For most symbolic variables and expressions,
erfinv returns unresolved symbolic calls:
syms x f = sin(x) + x*exp(x); erfinv(x) erfinv(f)
ans = erfinv(x) ans = erfinv(sin(x) + x*exp(x))
Inverse Error Function for Vectors and Matrices
If the input argument is a vector or a matrix,
erfinv returns the inverse error function for each element of that
vector or matrix.
Compute the inverse error function for elements of matrix M and
vector V:
M = sym([0 1 + i; 1/3 1]); V = sym([-1; inf]); erfinv(M) erfinv(V)
ans = [ 0, NaN] [ erfinv(1/3), Inf] ans = -Inf NaN
Special Values of Inverse Complementary Error Function
erfinv returns special values for particular
parameters.
Compute the inverse error function for x = –1, x = 0, and x = 1. The inverse error function has special values for these parameters:
[erfinv(-1), erfinv(0), erfinv(1)]
ans = -Inf 0 Inf
Handling Expressions That Contain Inverse Complementary Error Function
Many functions, such as diff and
int, can handle expressions containing
erfinv.
Compute the first and second derivatives of the inverse error function:
syms x diff(erfinv(x), x) diff(erfinv(x), x, 2)
ans = (pi^(1/2)*exp(erfinv(x)^2))/2 ans = (pi*exp(2*erfinv(x)^2)*erfinv(x))/2
Compute the integral of the inverse error function:
int(erfinv(x), x)
ans = -exp(-erfinv(x)^2)/pi^(1/2)
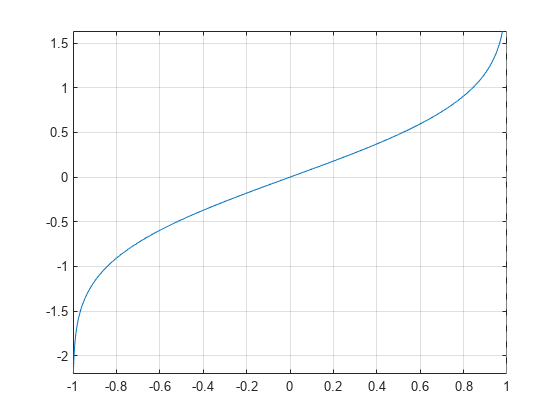
Plot Inverse Error Function
Plot the inverse error function on the interval from -1 to 1.
syms x fplot(erfinv(x),[-1,1]) grid on
Input Arguments
More About
Tips
Calling
erfinvfor a number that is not a symbolic object invokes the MATLAB®erfinvfunction. This function accepts real arguments only. If you want to compute the inverse error function for a complex number, usesymto convert that number to a symbolic object, and then callerfinvfor that symbolic object.If x < –1 or x > 1, or if x is complex, then
erfinv(x)returnsNaN.
Algorithms
The toolbox can simplify expressions that contain error functions and their inverses. For
real values x, the toolbox applies these simplification rules:
erfinv(erf(x)) = erfinv(1 - erfc(x)) = erfcinv(1 - erf(x)) = erfcinv(erfc(x)) = xerfinv(-erf(x)) = erfinv(erfc(x) - 1) = erfcinv(1 + erf(x)) = erfcinv(2 - erfc(x)) = -x
For any value x, the toolbox applies these simplification rules:
erfcinv(x) = erfinv(1 - x)erfinv(-x) = -erfinv(x)erfcinv(2 - x) = -erfcinv(x)erf(erfinv(x)) = erfc(erfcinv(x)) = xerf(erfcinv(x)) = erfc(erfinv(x)) = 1 - x
References
[1] Gautschi, W. “Error Function and Fresnel Integrals.” Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (M. Abramowitz and I. A. Stegun, eds.). New York: Dover, 1972.
Version History
Introduced in R2012a