dawson
Dawson integral
Syntax
Description
dawson( represents the Dawson
integral.X)
Examples
Dawson Integral for Numeric and Symbolic Arguments
Depending on its arguments, dawson
returns floating-point or exact symbolic results.
Compute the Dawson integrals for these numbers. Because these numbers are not
symbolic objects, dawson returns floating-point
results.
A = dawson([-Inf, -3/2, -1, 0, 2, Inf])
A =
0 -0.4282 -0.5381 0 0.3013 0Compute the Dawson integrals for the numbers converted to symbolic objects. For
many symbolic (exact) numbers, dawson returns unresolved
symbolic calls.
symA = dawson(sym([-Inf, -3/2, -1, 0, 2, Inf]))
symA = [ 0, -dawson(3/2), -dawson(1), 0, dawson(2), 0]
Use vpa to approximate symbolic results with
floating-point numbers:
vpa(symA)
ans = [ 0,... -0.42824907108539862547719010515175,... -0.53807950691276841913638742040756,... 0,... 0.30134038892379196603466443928642,... 0]
Plot the Dawson Integral
Plot the Dawson integral on the interval from -10 to 10.
syms x fplot(dawson(x),[-10 10]) grid on
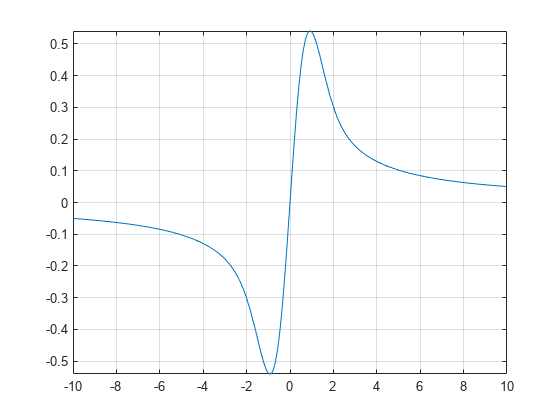
Handle Expressions Containing Dawson Integral
Many functions, such as diff and
limit, can handle expressions containing
dawson.
Find the first and second derivatives of the Dawson integral:
syms x diff(dawson(x), x) diff(dawson(x), x, x)
ans = 1 - 2*x*dawson(x) ans = 2*x*(2*x*dawson(x) - 1) - 2*dawson(x)
Find the limit of this expression involving dawson:
limit(x*dawson(x), Inf)
ans = 1/2
Input Arguments
More About
Tips
dawson(0)returns0.dawson(Inf)returns0.dawson(-Inf)returns0.
Version History
Introduced in R2014a