vartestn
Multiple-sample tests for equal variances
Syntax
Description
vartestn( returns
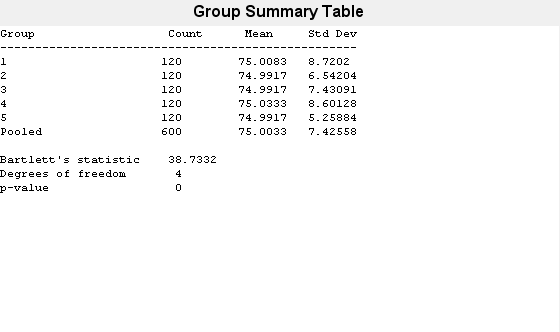
a summary table of statistics and a box plot for a Bartlett test of
the null hypothesis that the columns of data vector x)x come
from normal distributions with the same variance. The alternative
hypothesis is that not all columns of data have the same variance.
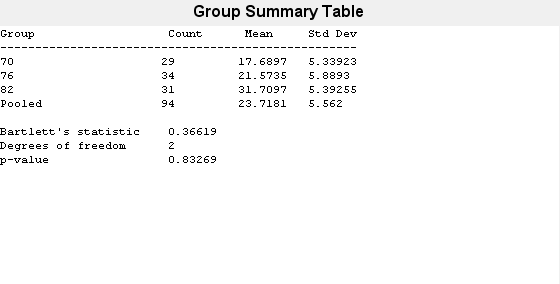
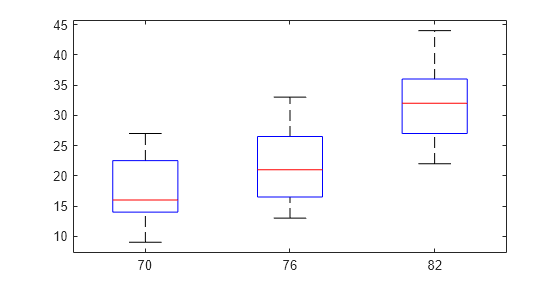
vartestn( returns
a summary table of statistics and a box plot for a test of unequal
variances with additional options specified by one or more name-value
pair arguments. For example, you can specify a different type of hypothesis
test or change the display settings for the test results.x,Name,Value)
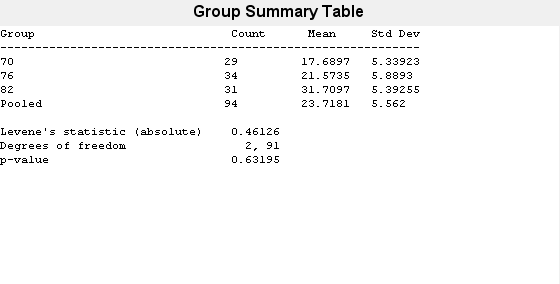
vartestn( returns
a summary table of statistics and a box plot for a test of unequal
variances with additional options specified by one or more name-value
pair arguments. For example, you can specify a different type of hypothesis
test or change the display settings for the test results.x,group,Name,Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Version History
Introduced before R2006a