ClassificationNeuralNetwork
Description
A ClassificationNeuralNetwork object is a trained neural
network for classification, such as a feedforward, fully connected network. In a
feedforward, fully connected network, the first fully connected layer of has a
connection from the network input (predictor data X), and
each subsequent layer has a connection from the previous layer. Each fully connected
layer multiplies the input by a weight matrix (LayerWeights) and then adds a bias vector (LayerBiases). An activation function follows each fully connected layer
(Activations
and OutputLayerActivation). The final fully connected layer and the
subsequent softmax activation function produce the network's output, namely
classification scores (posterior probabilities) and predicted labels. For more
information, see Neural Network Structure.
Creation
Create a ClassificationNeuralNetwork object by using fitcnet.
Properties
Neural Network Properties
This property is read-only.
Sizes of the fully connected layers in the neural network model.
The property value depends on the method used to fit the model.
For models fit using a
dlnetworkor layer array that specifies the neural network architecture, this property is empty. In this case, to examine the neural network architecture of the model, convert the model to adlnetworkobject using thedlnetwork(Deep Learning Toolbox) function.Otherwise, the property is a positive integer vector, where the ith element of
LayerSizesis the number of outputs in the ith fully connected layer of the neural network model. In this case,LayerSizesdoes not include the size of the final fully connected layer. This layer always has K outputs, where K is the number of classes in the response variable.
Data Types: single | double
This property is read-only.
Learned layer weights for the fully connected layers.
The property value depends on the method used to fit the model.
For models fit using a
dlnetworkor layer array that specifies the neural network architecture, this property is empty. In this case, to examine the learnable parameters of the model, convert the model to adlnetworkobject using thedlnetwork(Deep Learning Toolbox) function.Otherwise, the property is a cell array, where entry i in the cell array corresponds to the layer weights for the fully connected layer i. For example,
Mdl.LayerWeights{1}returns the weights for the first fully connected layer of the modelMdl. In this case,LayerWeightsincludes the weights for the final fully connected layer.
Data Types: cell
This property is read-only.
Learned layer biases for the fully connected layers.
The property value depends on the method used to fit the model.
For models fit using a
dlnetworkor layer array that specifies the neural network architecture, this property is empty. In this case, to examine the learnable parameters of the model, convert the model to adlnetworkobject using thedlnetwork(Deep Learning Toolbox) function.Otherwise, the property is a cell array, where entry i in the cell array corresponds to the layer biases for the fully connected layer i. For example,
Mdl.LayerBiases{1}returns the biases for the first fully connected layer of the modelMdl. In this case,LayerBiasesincludes the biases for the final fully connected layer.
Data Types: cell
This property is read-only.
Activation functions for the fully connected layers of the neural network model.
The property value depends on the method used to fit the model.
For models fit using a
dlnetworkor layer array that specifies the neural network architecture, this property is''. In this case, to examine the neural network architecture of the model, convert the model to adlnetworkobject using thedlnetwork(Deep Learning Toolbox) function.Otherwise, the property is a character vector or cell array of character vectors.
If
Activationscontains only one activation function, then it is the activation function for every fully connected layer of the neural network model, excluding the final fully connected layer, which is always softmax (OutputLayerActivation).If
Activationsis an array of activation functions, then the ith element is the activation function for the ith layer of the neural network model.
If Activations is a character vector or a cell array of character vectors, then the values are from this table.
| Value | Description |
|---|---|
"relu" | Rectified linear unit (ReLU) function — Performs a threshold operation on each element of the input, where any value less than zero is set to zero, that is, |
"tanh" | Hyperbolic tangent (tanh) function — Applies the |
"sigmoid" | Sigmoid function — Performs the following operation on each input element: |
"none" | Identity function — Returns each input element without performing any transformation, that is, f(x) = x |
Data Types: char | cell
This property is read-only.
Activation function for the final fully connected layer.
The property value depends on the method used to fit the model.
For models fit using a
dlnetworkor layer array that specifies the neural network architecture, this property is empty. In this case, to examine the neural network architecture of the model, convert the model to adlnetworkobject using thedlnetwork(Deep Learning Toolbox) function.Otherwise, the property is
'softmax'. The function takes each input xi and returns the following, where K is the number of classes in the response variable:The results correspond to the predicted classification scores (or posterior probabilities).
This property is read-only.
Parameter values used to train the
ClassificationNeuralNetwork model, returned as a
NeuralNetworkParams object.
ModelParameters contains parameter values such
as the name-value arguments used to train the neural network
classifier.
Access the properties of ModelParameters by using
dot notation. For example, access the function used to initialize the
fully connected layer weights of a model Mdl by using
Mdl.ModelParameters.LayerWeightsInitializer.
Convergence Control Properties
This property is read-only.
Convergence information, returned as a structure array.
| Field | Description |
|---|---|
Iterations | Number of training iterations used to train the neural network model |
TrainingLoss | Training cross-entropy loss for the returned
model, or
resubLoss(Mdl,'LossFun','crossentropy')
for model Mdl |
Gradient | Gradient of the loss function with respect to the weights and biases at the iteration corresponding to the returned model |
Step | Step size at the iteration corresponding to the returned model |
Time | Total time spent across all iterations (in seconds) |
ValidationLoss | Validation cross-entropy loss for the returned model |
ValidationChecks | Maximum number of times in a row that the validation loss was greater than or equal to the minimum validation loss |
ConvergenceCriterion | Criterion for convergence |
History | See TrainingHistory |
For models fit using a dlnetwork or layer array that
specifies the neural network architecture, the value for the
ValidationChecks is always
NaN.
Data Types: struct
This property is read-only.
Training history, returned as a table.
| Column | Description |
|---|---|
Iteration | Training iteration |
TrainingLoss | Training cross-entropy loss for the model at this iteration |
Gradient | Gradient of the loss function with respect to the weights and biases at this iteration |
Step | Step size at this iteration |
Time | Time spent during this iteration (in seconds) |
ValidationLoss | Validation cross-entropy loss for the model at this iteration |
ValidationChecks | Running total of times that the validation loss is greater than or equal to the minimum validation loss |
For models fit using a dlnetwork or layer array that
specifies the neural network architecture, the table does not include
the Time and ValidationChecks
columns.
Data Types: table
This property is read-only.
Solver used to train the neural network model, returned as
'LBFGS'. To create a
ClassificationNeuralNetwork model,
fitcnet uses a limited-memory
Broyden-Fletcher-Goldfarb-Shanno quasi-Newton algorithm (LBFGS) as its
loss function minimization technique, where the software minimizes the
cross-entropy loss.
Predictor Properties
This property is read-only.
Predictor variable names, returned as a cell array of character
vectors. The order of the elements of PredictorNames
corresponds to the order in which the predictor names appear in the
training data.
Data Types: cell
This property is read-only.
Categorical predictor indices,
returned as a vector of positive integers. Assuming that the predictor
data contains observations in rows,
CategoricalPredictors contains index values
corresponding to the columns of the predictor data that contain
categorical predictors. If none of the predictors are categorical, then
this property is empty ([]).
Data Types: double
This property is read-only.
Expanded predictor names, returned as a cell array of character
vectors. If the model uses encoding for categorical variables, then
ExpandedPredictorNames includes the names that
describe the expanded variables. Otherwise,
ExpandedPredictorNames is the same as
PredictorNames.
Data Types: cell
Since R2023b
This property is read-only.
Predictor means, returned as a numeric vector. If you set Standardize to
1 or true when
you train the neural network model, then the length of the
Mu vector is equal to the
number of expanded predictors (see
ExpandedPredictorNames). The
vector contains 0 values for dummy variables
corresponding to expanded categorical predictors.
If you set Standardize to 0 or false when you train the neural network model, then the Mu value is an empty vector ([]).
Data Types: double
Since R2023b
This property is read-only.
Predictor standard deviations, returned as a numeric vector. If you set
Standardize to 1 or true
when you train the neural network model, then the length of the
Sigma vector is equal to the number of expanded predictors (see
ExpandedPredictorNames). The vector contains
1 values for dummy variables corresponding to expanded
categorical predictors.
If you set Standardize to 0 or false when you train the neural network model, then the Sigma value is an empty vector ([]).
Data Types: double
This property is read-only.
Unstandardized predictors used to train the neural network model,
returned as a numeric matrix or table. X retains its
original orientation, with observations in rows or columns depending on
the value of the ObservationsIn name-value argument
in the call to fitcnet.
Data Types: single | double | table
Response Properties
This property is read-only.
Unique class names used in training, returned as a numeric vector,
categorical vector, logical vector, character array, or cell array of
character vectors. ClassNames has the same data type
as the class labels Y. (The software treats string arrays
as cell arrays of character vectors.)
ClassNames also determines the class order.
Data Types: single | double | categorical | logical | char | cell
This property is read-only.
Response variable name, returned as a character vector.
Data Types: char
This property is read-only.
Class labels used to train the model, returned as a numeric vector,
categorical vector, logical vector, character array, or cell array of
character vectors. Y has the same data type as the
response variable used to train the model. (The software treats string arrays
as cell arrays of character vectors.)
Each row of Y represents the classification of the
corresponding observation in X.
Data Types: single | double | categorical | logical | char | cell
Other Data Properties
This property is read-only.
Cross-validation optimization of hyperparameters, specified as a BayesianOptimization object or a table of hyperparameters and associated
values. This property is nonempty if the 'OptimizeHyperparameters'
name-value pair argument is nonempty when you create the model. The value of
HyperparameterOptimizationResults depends on the setting of the
Optimizer field in the
HyperparameterOptimizationOptions structure when you create the
model.
Value of Optimizer Option | Value of HyperparameterOptimizationResults |
|---|---|
"bayesopt" (default) | Object of class BayesianOptimization |
"gridsearch" or "randomsearch" | Table of hyperparameters used, observed objective function values (cross-validation loss), and rank of observations from lowest (best) to highest (worst) |
This property is read-only.
Number of observations in the training data stored in
X and Y, returned as a
positive numeric scalar.
Data Types: double
This property is read-only.
Observations of the original training data stored in the model,
returned as a logical vector. This property is empty if all observations
are stored in X and Y.
Data Types: logical
This property is read-only.
Observation weights used to train the model, returned as an
n-by-1 numeric vector. n is
the number of observations
(NumObservations).
The software normalizes the observation weights specified in the
Weights name-value argument so that the
elements of W within a particular class sum up to the
prior probability of that class.
Data Types: single | double
Other Classification Properties
Misclassification cost, returned as a numeric square matrix, where
Cost(i,j) is the cost of classifying a point into
class j if its true class is i.
The cost matrix always has this form: Cost(i,j) = 1
if i ~= j, and Cost(i,j) = 0 if
i = j. The rows correspond to the true class and
the columns correspond to the predicted class. The order of the rows and
columns of Cost corresponds to the order of the
classes in ClassNames.
The software uses the Cost value for prediction,
but not training. You can change the Cost property
value of the trained model by using dot notation.
Data Types: double
This property is read-only.
Prior class probabilities, returned as a numeric vector. The order of
the elements of Prior corresponds to the elements
of ClassNames.
Data Types: double
Score transformation, specified as a character vector or function handle. ScoreTransform represents a built-in transformation function or a function handle for transforming predicted classification scores.
To change the score transformation function to function, for example, use dot notation.
For a built-in function, enter a character vector.
Mdl.ScoreTransform = 'function';
This table describes the available built-in functions.
Value Description 'doublelogit'1/(1 + e–2x) 'invlogit'log(x / (1 – x)) 'ismax'Sets the score for the class with the largest score to 1, and sets the scores for all other classes to 0 'logit'1/(1 + e–x) 'none'or'identity'x (no transformation) 'sign'–1 for x < 0
0 for x = 0
1 for x > 0'symmetric'2x – 1 'symmetricismax'Sets the score for the class with the largest score to 1, and sets the scores for all other classes to –1 'symmetriclogit'2/(1 + e–x) – 1 For a MATLAB® function or a function that you define, enter its function handle.
Mdl.ScoreTransform = @function;
functionmust accept a matrix (the original scores) and return a matrix of the same size (the transformed scores).
Data Types: char | function_handle
Object Functions
compact | Reduce size of machine learning model |
crossval | Cross-validate machine learning model |
dlnetwork (Deep Learning Toolbox) | Deep learning neural network |
lime | Local interpretable model-agnostic explanations (LIME) |
partialDependence | Compute partial dependence |
plotPartialDependence | Create partial dependence plot (PDP) and individual conditional expectation (ICE) plots |
shapley | Shapley values |
resubEdge | Resubstitution classification edge |
resubLoss | Resubstitution classification loss |
resubMargin | Resubstitution classification margin |
resubPredict | Classify training data using trained classifier |
compareHoldout | Compare accuracies of two classification models using new data |
testckfold | Compare accuracies of two classification models by repeated cross-validation |
gather | Gather properties of Statistics and Machine Learning Toolbox object from GPU |
Examples
Train a neural network classifier, and assess the performance of the classifier on a test set.
Read the sample file CreditRating_Historical.dat into a table. The predictor data consists of financial ratios and industry sector information for a list of corporate customers. The response variable consists of credit ratings assigned by a rating agency. Preview the first few rows of the data set.
creditrating = readtable("CreditRating_Historical.dat");
head(creditrating) ID WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry Rating
_____ ______ ______ _______ ________ _____ ________ _______
62394 0.013 0.104 0.036 0.447 0.142 3 {'BB' }
48608 0.232 0.335 0.062 1.969 0.281 8 {'A' }
42444 0.311 0.367 0.074 1.935 0.366 1 {'A' }
48631 0.194 0.263 0.062 1.017 0.228 4 {'BBB'}
43768 0.121 0.413 0.057 3.647 0.466 12 {'AAA'}
39255 -0.117 -0.799 0.01 0.179 0.082 4 {'CCC'}
62236 0.087 0.158 0.049 0.816 0.324 2 {'BBB'}
39354 0.005 0.181 0.034 2.597 0.388 7 {'AA' }
Because each value in the ID variable is a unique customer ID, that is, length(unique(creditrating.ID)) is equal to the number of observations in creditrating, the ID variable is a poor predictor. Remove the ID variable from the table, and convert the Industry variable to a categorical variable.
creditrating = removevars(creditrating,"ID");
creditrating.Industry = categorical(creditrating.Industry);Convert the Rating response variable to a categorical variable.
creditrating.Rating = categorical(creditrating.Rating, ... ["AAA","AA","A","BBB","BB","B","CCC"]);
Partition the data into training and test sets. Use approximately 80% of the observations to train a neural network model, and 20% of the observations to test the performance of the trained model on new data. Use cvpartition to partition the data.
rng("default") % For reproducibility of the partition c = cvpartition(creditrating.Rating,"Holdout",0.20); trainingIndices = training(c); % Indices for the training set testIndices = test(c); % Indices for the test set creditTrain = creditrating(trainingIndices,:); creditTest = creditrating(testIndices,:);
Train a neural network classifier by passing the training data creditTrain to the fitcnet function.
Mdl = fitcnet(creditTrain,"Rating")Mdl =
ClassificationNeuralNetwork
PredictorNames: {'WC_TA' 'RE_TA' 'EBIT_TA' 'MVE_BVTD' 'S_TA' 'Industry'}
ResponseName: 'Rating'
CategoricalPredictors: 6
ClassNames: [AAA AA A BBB BB B CCC]
ScoreTransform: 'none'
NumObservations: 3146
LayerSizes: 10
Activations: 'relu'
OutputLayerActivation: 'softmax'
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [1000×7 table]
Properties, Methods
Mdl is a trained ClassificationNeuralNetwork classifier. You can use dot notation to access the properties of Mdl. For example, you can specify Mdl.TrainingHistory to get more information about the training history of the neural network model.
Evaluate the performance of the classifier on the test set by computing the test set classification error. Visualize the results by using a confusion matrix.
testAccuracy = 1 - loss(Mdl,creditTest,"Rating", ... "LossFun","classiferror")
testAccuracy = 0.8002
confusionchart(creditTest.Rating,predict(Mdl,creditTest))

Specify a custom neural network architecture using Deep Learning Toolbox™.
Load the ionosphere data set, which includes radar signal data. X contains the predictor data, and Y is the response variable, whose values represent either good ("g") or bad ("b") radar signals.
load ionosphereSeparate the data into training data (XTrain and YTrain) and test data (XTest and YTest) by using a stratified holdout partition. Reserve approximately 30% of the observations for testing, and use the rest of the observations for training.
rng("default") % For reproducibility of the partition cvp = cvpartition(Y,Holdout=0.3); XTrain = X(training(cvp),:); YTrain = Y(training(cvp)); XTest = X(test(cvp),:); YTest = Y(test(cvp));
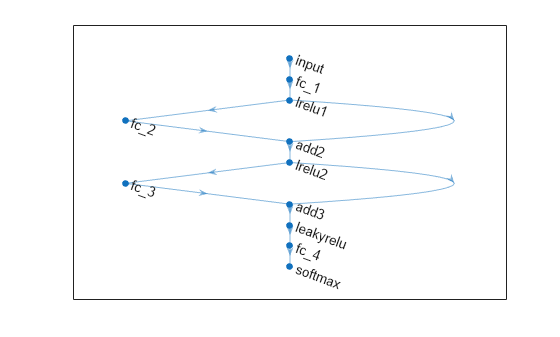
Define a neural network architecture with these characteristics:
A feature input layer with an input size that matches the number of predictors.
Three fully connected layers followed by leaky ReLU layers, connected in series, where the fully connected layers have output sizes of 16, and addition layers after the second and third fully connected layers.
Skip connections around the second and third fully connected layers using the addition layers.
A final fully connected layer with an output size that matches the number of classes followed by a softmax layer.
inputSize = size(XTrain,2);
outputSize = numel(unique(YTrain));
net = dlnetwork;
layers = [
featureInputLayer(inputSize)
fullyConnectedLayer(30)
leakyReluLayer(Name="lrelu1")
fullyConnectedLayer(30)
additionLayer(2,Name="add2")
leakyReluLayer(Name="lrelu2")
fullyConnectedLayer(30)
additionLayer(2,Name="add3")
leakyReluLayer
fullyConnectedLayer(outputSize)
softmaxLayer];
net = addLayers(net,layers);
net = connectLayers(net,"lrelu1","add2/in2");
net = connectLayers(net,"lrelu2","add3/in2");Visualize the neural network architecture in a plot.
figure plot(net)
Train a neural network classifier.
Mdl = fitcnet(XTrain,YTrain,Network=net,Standardize=true)
Mdl =
ClassificationNeuralNetwork
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'b' 'g'}
ScoreTransform: 'none'
NumObservations: 246
LayerSizes: []
Activations: ''
OutputLayerActivation: ''
Solver: 'LBFGS'
ConvergenceInfo: [1×1 struct]
TrainingHistory: [30×5 table]
View network information using dlnetwork.
Properties, Methods
To estimate the performance of the trained classifier, compute the test set classification error.
testError = loss(Mdl,XTest,YTest, ... LossFun="classiferror")
testError = 0.0774
Extended Capabilities
Usage notes and limitations:
The
predictobject function supports code generation for models not fit using adlnetworkor layer array that specifies the neural network architecture.
For more information, see Introduction to Code Generation.
Usage notes and limitations:
The following object functions fully support GPU arrays:
The object functions execute on a GPU if at least one of the following applies:
The model was fitted with GPU arrays.
The predictor data that you pass to the object function is a GPU array.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2021aConvert a ClassificationNeuralNetwork object to a dlnetwork (Deep Learning Toolbox) object using the dlnetwork function. Use
dlnetwork objects to make further edits and customize the underlying
neural network of a ClassificationNeuralNetwork object and retrain it using the trainnet (Deep Learning Toolbox)
function or a custom training loop.
Starting in R2023b, training observations with missing predictor values are included in the X, Y, and W data properties. The RowsUsed property indicates the training observations stored in the model, rather than those used for training. Observations with missing predictor values continue to be omitted from the model training process.
In previous releases, the software omitted training observations that contained missing predictor values from the data properties of the model.
Neural network models include Mu and Sigma properties that contain the means and standard deviations, respectively, used to standardize the predictors before training. The properties are empty when the fitting function does not perform any standardization.
fitcnet supports misclassification costs and prior probabilities for
neural network classifiers. Specify the Cost and
Prior name-value arguments when you create a model. Alternatively,
you can specify misclassification costs after training a model by using dot notation to
change the Cost property value of the
model.
Mdl.Cost = [0 2; 1 0];
See Also
fitcnet | predict | loss | margin | edge | ClassificationPartitionedModel | CompactClassificationNeuralNetwork | dlnetwork (Deep Learning Toolbox)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)