Bernoulli Distribution
Overview
The Bernoulli distribution is a discrete probability distribution with only two possible values for the random variable. Each instance of an event with a Bernoulli distribution is called a Bernoulli trial.
Parameters
The Bernoulli distribution uses the following parameter.
| Parameter | Description | Support |
|---|---|---|
p | Probability of success |
Probability Density Function
The probability density function (pdf) of the Bernoulli distribution is
For discrete distributions, the pdf is also known as the probability mass function (pmf).
For an example, see Compute Bernoulli Distribution pdf.
Cumulative Distribution Function
The cumulative distribution function (cdf) of the Bernoulli distribution is
For an example, see Compute Bernoulli Distribution cdf.
Descriptive Statistics
The mean of the Bernoulli distribution is p.
The variance of the Bernoulli distribution is p(1 – p).
Examples
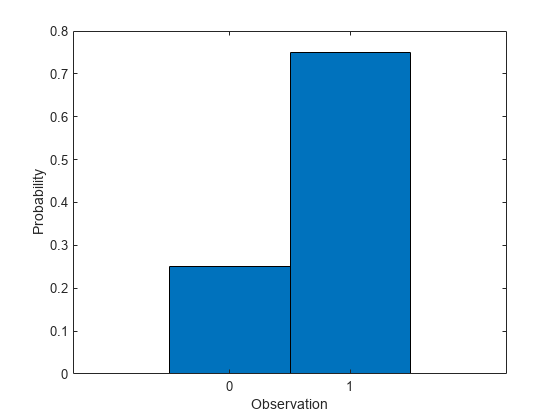
Compute Bernoulli Distribution pdf
The Bernoulli distribution is a special case of the binomial distribution, where N = 1. Use binopdf to compute the pdf of the Bernoulli distribution with the probability of success 0.75.
p = 0.75; x = 0:1; y = binopdf(0:1,1,p);
Plot the pdf with bars of width 1.
figure bar(x,y,1) xlabel('Observation') ylabel('Probability')
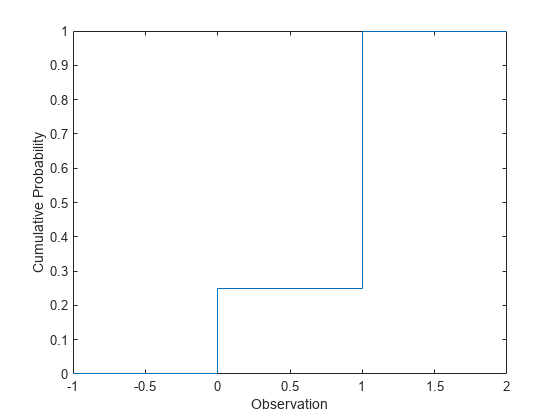
Compute Bernoulli Distribution cdf
The Bernoulli distribution is a special case of the binomial distribution, where N = 1. Use binocdf to compute the cdf of the Bernoulli distribution with the probability of success 0.75.
p = 0.75; y = binocdf(-1:2,1,p);
Plot the cdf.
figure stairs(-1:2,y) xlabel('Observation') ylabel('Cumulative Probability')
Related Distributions
Binomial Distribution — The binomial distribution is a two-parameter discrete distribution that models the total number of successes in repeated Bernoulli trials. The Bernoulli distribution occurs as a binomial distribution with N = 1.
Geometric Distribution — The geometric distribution is a one-parameter discrete distribution that models the total number of failures before the first success in repeated Bernoulli trials.
References
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.