Measure Temperature During Quenching of Steel Using Thermocouple Block

Open Live Script

This example shows how to use the Thermocouple block to measure the temperature of steel during quenching. During quenching, you heat the steel to a temperature above its recrystallization temperature and then rapidly cool the steel by submerging it in liquid. Because of the high temperature, you cannot use traditional temperature measurement apparatus such as thermistor-based or semiconductor-based temperature sensors or liquid thermometers. To measure temperatures in such harsh environments, industries and laboratories employ thermocouples, which convert thermal potential difference to electrical potential difference.

Model Overview

Open the ee_thermocouple_quenching model.

In this model, a Thermal Mass block models a steel cylinder with an initial temperature of 850°C. A Constant Volume Chamber (TL) block models a quenching bath and cools the cylinder to 20°C through forced convection.

myModel = "ee_thermocouple_quenching";
open_system(myModel)

Simulate Model and Plot Results

Simulate the model.

sim(myModel);

The 1-D Lookup Table block allows you to estimate the temperature of the Thermocouple block as a function of the corresponding voltage. Plot the estimated temperature of the thermocouple and the actual simulated temperature of the cylinder against time. The estimated and actual values are consistent.

TemperatureOut = squeeze(logsout{1}.Values.Data);
time = simlog_ee_thermocouple_quenching.Cylinder.T.series.time;
temperature = simlog_ee_thermocouple_quenching.Cylinder.T.series.values;

ee_thermocouple_quenching_plot(tout,TemperatureOut,time,temperature,"Temperature (°C)","Estimate","Actual")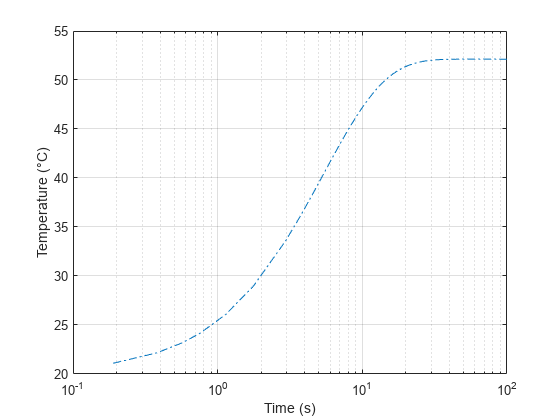

Plot the temperature of the liquid inside the chamber.

time =  simlog_ee_thermocouple_quenching.Constant_Volume_Chamber_TL.T_I.series.time;
temperature =  simlog_ee_thermocouple_quenching.Constant_Volume_Chamber_TL.T_I.series.values;

ee_thermocouple_quenching_plot(time,temperature,"Temperature (°C)")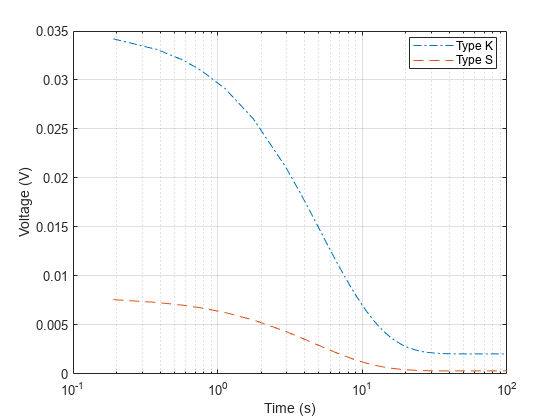

The properties of the thermal liquid, such as density, specific internal energy and specific heat, are tabulated against both temperature and pressure in the Thermal Liquid Settings (TL) block. To ensure that the temperature of the liquid does not exceed the maximum valid temperature of the model, you must set the Chamber volume and Cross-sectional area at port A parameters of the Constant Volume Chamber (TL) to sufficiently high values. If the temperature exceeds the maximum valid temperature, you receive this error message: "Temperature of liquid volume must be less than or equal to Maximum valid temperature". In this example, the highest temperature the liquid reaches is 52.1°C (325.3 K), which is within the acceptable range. Extract the value and unit of the Maximum valid temperature parameter of the Thermal Liquid Settings block to confirm this.

maximumValidTemperature = get_param(myModel+"/Thermal Liquid Settings (TL)","T_max")

maximumValidTemperature = 
'363.16'

maximumValidTemperatureUnit = get_param(myModel+"/Thermal Liquid Settings (TL)","T_max_unit")

maximumValidTemperatureUnit = 
'K'

Change to Thermocouple Type S

The Thermocouple block parameters correspond to a Type K thermocouple. These values are available in the NIST ITS-90 Thermocouple Database [1].

Save the results for the Type K thermocouple.

TypeK_tout = tout;
TypeK_TemperatureOut = squeeze(logsout{1}.Values.Data);
TypeK_vout = simlog_ee_thermocouple_quenching.Thermocouple.v.series.values;

In the Thermocouple block, set the Thermocouple type parameter to Type B, E, J, K (t<=0 degC), N, R, S or T.

set_param(myModel+"/Thermocouple","thermocouple_type","1");

Set the values of the Coefficients [c0 c1 ... cn] parameter for a Type S thermocouple.

set_param(myModel+"/Thermocouple","Cvec","TypeS_Cvec");

In the 1-D Lookup Table block, set the Table data and Breakpoints 1 parameters to the correct values for a Type S thermocouple.

For more information about how to obtain these vectors, see Approximating Nonlinear Relationships: Type S Thermocouple.

set_param(myModel+"/1-D Lookup Table","Table","TypeS_degC");
set_param(myModel+"/1-D Lookup Table","BreakpointsForDimension1","TypeS_Volts");

Simulate the model again and save the results.

sim(myModel);

TypeS_tout = tout;
TypeS_TemperatureOut = squeeze(logsout{1}.Values.Data);
TypeS_vout = simlog_ee_thermocouple_quenching.Thermocouple.v.series.values;

Plot the output voltage and temperature for the Type K and Type S Thermocouples. The output voltage differs for the two thermocouple types but the temperatures are consistent.

ee_thermocouple_quenching_plot(TypeK_tout,TypeK_vout,TypeS_tout,TypeS_vout,"Voltage (V)","Type K","Type S")

ee_thermocouple_quenching_plot(TypeK_tout,TypeK_TemperatureOut,TypeS_tout,TypeS_TemperatureOut,"Temperature (°C)","Type K","Type S")

Change Heat Transfer Properties

In this example, the Specific heat coefficient parameter of the Thermal Mass block and the Heat transfer coefficient of the Convective Heat Transfer block are estimates from a scale-model laboratory study of industrial quenching of a steel cylinder in water [2]. For simplicity, these parameters are constant. For more accurate simulation results, specify these coefficients as functions of the temperature if the data are available. Alternatively, run simulations with different values of these parameters to obtain a range of estimates.

In the Convective Heat Transfer block, set the Heat transfer coefficient parameter to 2000.

set_param(myModel+"/Convective Heat Transfer","heat_tr_coeff","2000");

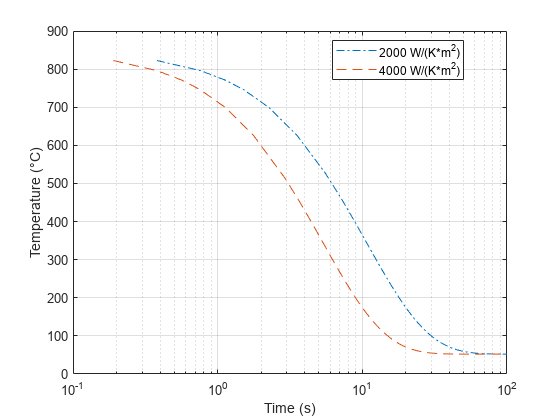
Simulate the model and plot the results. With a heat transfer coefficient of 2000 W/(K*m^2), the steel cylinder cools much more slowly.

sim(myModel);
TemperatureOut = squeeze(logsout{1}.Values.Data);

ee_thermocouple_quenching_plot(tout,TemperatureOut,TypeS_tout,TypeS_TemperatureOut,"Temperature (°C)","2000 W/(K*m^2)","4000 W/(K*m^2)")

References

[1] Garrity, Karen. “NIST ITS-90 Thermocouple Database - SRD 60.” National Institute of Standards and Technology, July 1, 2000. https://doi.org/10.18434/T4S888.

[2] Hasan, H. S., M. J. Peet, J. M. Jalil, and H. K. D. H. Bhadeshia. “Heat Transfer Coefficients during Quenching of Steels.” Heat and Mass Transfer 47, no. 3 (March 2011): 315–21. https://doi.org/10.1007/s00231-010-0721-4.