How the Optimization Algorithm Formulates Minimization Problems

When you optimize parameters of a Simulink^® model to meet design requirements, Simulink Design Optimization™ software automatically converts the requirements into a constrained optimization problem and then solves the problem using optimization techniques. The constrained optimization problem iteratively simulates the Simulink model, compares the results of the simulations with the constraint objectives, and uses optimization methods to adjust tuned parameters to better meet the objectives.

This topic describes how the software formulates the constrained optimization problem used by the optimization algorithms. For each optimization algorithm, the software formulates one of the following types of minimization problems:

• Feasibility

• Tracking

• Mixed feasibility and tracking

For more information on how each optimization algorithm formulates these problems, see:

• Gradient Descent Method Problem Formulations

• Simplex Search Method Problem Formulations

• Pattern Search Method Problem Formulations

• Gradient Computations

Feasibility Problem and Constraint Formulation

Feasibility means that the optimization algorithm finds parameter values that satisfy all constraints to within specified tolerances but does not minimize any objective or cost function in doing so.

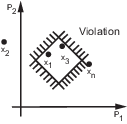
In the following figure, x₁, x₃, and x_n represent a combination of parameter values P₁ and P₂ and are feasible solutions because they do not violate the lower bound constraint.

In a Simulink model, you constrain a signal by specifying lower and upper bounds in a Check block (Check Step Response Characteristics, ...) or a requirement object (sdo.requirements.StepResponseEnvelope, ...), as shown in the following figure.

These constraints are piecewise linear bounds. A piecewise linear bound y_bnd with n edges can be represented as:

$$y_{bnd}(t)=\{\begin{array}{cc}{y}_1(t)& t_1\le t\le t_2\\ y_2(t)& t_2\le t\le t_3\\ ⋮& ⋮\\ y_n(t)& t_n\le t\le t_{n+1}\end{array},$$

The software computes the signed distance between the simulated response and the edge. The signed distance for lower bounds is:

$$\begin{array}{l}c=\left[\begin{array}{l}\underset{t_1\le t\le t_2}{\max }{y}_{bnd}-y_{sim}\\ \underset{t_2\le t\le t_3}{\max }{y}_{bnd}-y_{sim}\\ \underset{t_n\le t\le t_{n+1}}{\max }{y}_{bnd}-y_{sim}\end{array}\right],\\ \end{array}$$

where y_sim is the simulated response and is a function of the parameters being optimized.

The signed distance for upper bounds is:

$$c=\left[\begin{array}{c}\underset{t_1\le t\le t_2}{\max }{y}_{sim}-y_{bnd}\\ \underset{t_2\le t\le t_3}{\max }{y}_{sim}-y_{bnd}\\ \underset{t_n\le t\le t_{n+1}}{\max }{y}_{sim}-y_{bnd}\end{array}\right].$$

At the command line, optimFcn supplies c directly from the Cleq field of vals.

If all the constraints are met (c ≤ 0) for some combination of parameter values, then that solution is said to be feasible. In the following figure, x₁ and x₃ are feasible solutions.

When your model has multiple requirements or vector signals feeding a requirement, the constraint vector is extended with the constraint violations for each signal and bound:

$$C=\left[c_1;c_2;\cdots ;c_n\right].$$

Tracking Problem

In addition to lower and upper bounds, you can specify a reference signal in a Check Against Reference block or sdo.requirements.SignalTracking object, which the Simulink model output can track. The tracking objective is a sum-squared-error tracking objective.

You specify the reference signal as a sequence of time-amplitude pairs:

$$y_{ref}(t_{ref}),t_{ref}\in \{T_{ref0},T_{ref1},\cdots ,T_{refN}\}.$$

The software computes the simulated response as a sequence of time-amplitude pairs:

$$y_{sim}(t_{sim}),t_{sim}\in \{T_{sim0},T_{sim1},\cdots ,T_{simN}\},$$

where some values of t_sim may match the values of t_ref.

A new time base, t_new, is formed from the union of the elements of t_ref and t_sim. Elements that are not within the minimum-maximum range of both t_ref and t_sim are omitted:

$$t_{new}=\{t:t_{sim}\cup t_{ref}\}$$

Using linear interpolation, the software computes the values of y_ref and y_sim at the time points in t_new and then computes the scaled error:

$$e(t_{new})=\frac{\left(y_{sim}(t_{new})-y_{ref}(t_{new})\right)}{\underset{t_{new}}{\max }\left|y_{ref}\right|}.$$

Finally, the software computes the weighted, integral square error:

$$f={\displaystyle \int w\left(t\right)e{(t)}^{2}dt}.$$

Note

The weight w(t) is 1 by default. You can specify a different value of weight only at the command line.

When your model has requirements or vector signals feeding a requirement, the tracking objective equals the sum of the individual tracking integral errors for each signal:

$$F={\displaystyle \sum f_i}.$$

Gradient Descent Method Problem Formulations

The Gradient Descent method uses the function fmincon to optimize model parameters to meet design requirements.

Problem Type	Problem Formulation
Feasibility Problem	The software formulates the constraint C(x) as described in Feasibility Problem and Constraint Formulation. If you select the maximally feasible solution option (i.e., the optimization continues after an initial feasible solution is found), the software uses the following problem formulation: $$\begin{array}{l}\underset{\left[x,\gamma \right]}{\min }\gamma \\ s.t.C(x)\le \gamma \\ \underset{¯}{x}\le x\le \overline{x}\\ \gamma \le 0\end{array}$$ γ is a slack variable that permits a feasible solution with C(x) ≤ γ rather than C(x) ≤ 0. If you do not select the maximally feasible solution option (i.e., the optimization terminates as soon as a feasible solution is found), the software uses the following problem formulation: $$\begin{array}{l}\underset{x}{\min }\text{ 0}\\ s.t.C(x)\le 0\\ \underset{¯}{x}\le x\le \overline{x}\end{array}$$
Tracking Problem	The software formulates the tracking objective F(x) as described in Tracking Problem and minimizes the tracking objective: $$\begin{array}{l}\underset{x}{\min }F(x)\\ s.t.\underset{¯}{x}\le x\le \overline{x}\end{array}$$
Mixed Feasibility and Tracking Problem	The software minimizes following problem formulation: $$\begin{array}{l}\underset{x}{\min }F(x)\\ s.t.C(x)\le 0\\ \underset{¯}{x}\le x\le \overline{x}\end{array}$$ Note When tracking a reference signal, the software ignores the maximally feasible solution option.

Simplex Search Method Problem Formulations

The Simplex Search method uses the function fminsearch and fminbnd to optimize model parameters to meet design requirements. fminbnd is used if one scalar parameter is being optimized, otherwise fminsearch is used. You cannot use parameter bounds $$\underset{¯}{x}\le x\le \overline{x}$$ with fminsearch.

Problem Type	Problem Formulation
Feasibility Problem	The software formulates the constraint C(x) as described in Feasibility Problem and Constraint Formulation and then minimizes the maximum constraint violation: $$\underset{x}{\min }\text{ max}\left(C\left(x\right)\right)$$
Tracking Problem	The software formulates the tracking objective F(x) as described in Tracking Problem and then minimizes the tracking objective: $$\underset{x}{\min }F(x)$$
Mixed Feasibility and Tracking Problem	The software formulates the problem in two steps: Finds a feasible solution. $$\underset{x}{\min }\text{ max}\left(C\left(x\right)\right)$$ Minimizes the tracking objective. The software uses the results from step 1 as initial guesses and maintains feasibility by introducing a discontinuous barrier in the optimization objective. $$\begin{array}{l}\underset{x}{\min }\Gamma \left(x\right)\\ \text{where}\\ \Gamma (x)=\{\begin{array}{ll}\infty \hfill & \text{if}\max \left(C(x)\right)>0\hfill \\ F(x)\hfill & \text{otherwise}\text{.}\hfill \end{array}\end{array}$$

Pattern Search Method Problem Formulations

The Pattern Search method uses the function patternsearch (Global Optimization Toolbox) to optimize model parameters to meet design requirements.

Problem Type	Problem Formulation
Feasibility Problem	The software formulates the constraint C(x) as described in Feasibility Problem and Constraint Formulation and then minimizes the maximum constraint violation: $$\begin{array}{l}\underset{x}{\min }\text{ max}\left(C\left(x\right)\right)\\ s.t.\underset{¯}{x}\le x\le \overline{x}\end{array}$$
Tracking Problem	The software formulates the tracking objective F(x) as described in Tracking Problem and then minimizes the tracking objective: $$\begin{array}{l}\underset{x}{\min }F(x)\\ s.t.\underset{¯}{x}\le x\le \overline{x}\end{array}$$
Mixed Feasibility and Tracking Problem	The software formulates the problem in two steps: Finds a feasible solution. $$\begin{array}{l}\underset{x}{\min }\text{ max}\left(C\left(x\right)\right)\\ s.t.\underset{¯}{x}\le x\le \overline{x}\end{array}$$ Minimizes the tracking objective. The software uses the results from step 1 as initial guesses and maintains feasibility by introducing a discontinuous barrier in the optimization objective. $$\begin{array}{l}\underset{x}{\min }\Gamma (x)\\ s.t.\underset{¯}{x}\le x\le \overline{x}\\ \text{where}\\ \Gamma (x)=\{\begin{array}{ll}\infty \hfill & \text{if}\max \left(C(x)\right)>0\hfill \\ F(x)\hfill & \text{otherwise}\text{.}\hfill \end{array}\end{array}$$

Gradient Computations

For the Gradient descent (fmincon) optimization solver, the gradients are computed using numerical perturbation:

$$\begin{array}{l}dx=\sqrt[3]{eps}\times \max \left(\left|x\right|,\frac{1}{10}{x}_{typical}\right)\\ dL=\max \left(x-dx,x_{\min }\right)\\ dR=\min \left(x+dx,x_{\max }\right)\\ F_L=opt\_fcn(dL)\\ F_R=opt\_fcn(dR)\\ \frac{dF}{dx}=\frac{\left(F_L-F_R\right)}{\left(dL-dR\right)}\\ \end{array}$$

• x is a scalar design variable.

• x_min is the lower bound of x.

• x_max is the upper bound of x.

• x_typical is the scaled value of x.

• opt_fcn is the objective function.

dx is relatively large to accommodate simulation solver tolerances.

If you want to compute the gradients in any other way, you can do so in the cost function you write for performing design optimization programmatically. See sdo.optimize and GradFcn of sdo.OptimizeOptions for more information.