Design PID Controller Using Plant Frequency Response Near Bandwidth
This example shows one of several ways to tune a PID controller for plants that cannot be linearized. In this example, you use the Frequency Response Based PID Tuner to automatically characterize the frequency response of a buck converter around the control bandwidth and then tune the PID controller.
Buck Converter Model
Buck converters convert DC to DC. The model in this example uses a switching power supply to convert a 30V DC supply into a regulated DC supply. The converter is modeled using MOSFETs rather than ideal switches to ensure that device on-resistances are correctly represented. The converter response from reference voltage to measured voltage includes the MOSFET switches. Traditional PID design requires a linear model of the system from the "reference voltage" (controller output) to measured voltage. However, because of the switches in this model, automated linearization results in a zero system. When a model linearizes to zero, several alternatives are available.
Relinearize the system. Linearize the model at a different operating point or simulation snapshot time.
Identify a new plant. Use measured or simulated data to identify a plant model (requires System Identification Toolbox™ software).
Frequency response based tuning. Use simulated data to obtain the frequency response for the plant.
For this example, use the Frequency Response Based PID Tuner to estimate the frequency responses of the system and tune the PID controller. For an example that uses system identification to identify a plant model, see Design PID Controller Using Simulated I/O Data.
For more information on creating a buck converter model, see Buck Converter (Simscape Electrical).
open_system("scdbuckconverter")

The model uses a reference voltage that switches from 15 to 25 Volts at 0.004 seconds and a load current that is active from 0.0025 to 0.005 seconds. The controller is initialized with default gains that produce overshoot and a slow settling time. Simulating the model shows the underdamping and slow response of the system.
sim("scdbuckconverter") open_system("scdbuckconverter/Scope 1") open_system("scdbuckconverter/Scope 2")


For this example, improve the bandwidth and phase margin of the system to achieve better performance by characterizing the system using frequency response estimation and tuning the PID gains. When tuning the PID controller, consider the following characteristics of the buck converter system.
No system process or sensor noise
Controller input is the PWM signal
PWM signal is limited (saturated) to be between 0 and 1
Nominal output of the controller at steady-state is 0.5
For buck converter systems, it is desired to have a system with a low rise time and low overshoot. For this example, tune the controller to achieve a rise time of 250e-6 seconds and an overshoot of less than 10%.
Open Frequency Response Based PID Tuner
Open the Feedback controller subsystem and then open the PID Controller block dialog box. In Select Tuning Method, select Frequency Response Based and click Tune. The Frequency Response Based PID Tuner opens for the buck converter controller.
The Frequency Response Based PID Tuner automatically tunes a PID controller for the plant using two simulations. The first simulation generates a baseline response. The second simulation breaks the loop at the plant input, and perturbs the plant with sine and step signals. The tuner takes the difference between the two simulated responses, which removes the effect of any disturbances in the model. The tuner then uses the resulting data to estimate the plant frequency response. Finally, it uses the estimated frequency response to compute PID gains.
When you open the Frequency Response Based PID Tuner, it reads parameters from the PID Controller block to determine the structure of your PID controller. These parameters include:
PID Controller Type (P, I, PI, PID etc.)
PID Controller Form (Parallel, Ideal)
Integrator Method, if applicable (Forward Euler, Trapezoidal etc.)
Derivative Filter Method, if applicable (Forward Euler, Trapezoidal etc.)
Sample Time, if applicable
Specify Experiment Settings
Before tuning, specify parameters of the experiment the tuner performs to estimate the frequency response of the plant.

Start time is the time, in seconds, at which the tuner begins applying the perturbation signals to the plant. Choose a start time at which the plant is at the nominal operating point you want to use for tuning. For this example, the buck converter has an initial transient that falls off by 0.002 seconds. Therefore, enter 0.002 for Start Time.
Specify the Duration of the perturbation experiment. A conservative estimate for the duration of the experiment is 100 divided by the target bandwidth. The target bandwidth is approximately 2/τ, where τ is the desired rise time. For this example, the desired rise time is 250e-6 seconds which results in a target bandwidth of 8000 radians per second. In this example, a conservative estimate for the duration would then be 100/8000 or 0.0125 seconds. Choose 0.0125 seconds for the Duration.
During the experiment, the tuner injects sinusoidal signals into the plant at four frequencies, [1/3, 1, 3, 10] 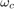 , where
, where 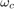 is the target bandwidth you specify for tuning. Specify the amplitudes of the injected sine waves in the Sine Amplitudes field.
is the target bandwidth you specify for tuning. Specify the amplitudes of the injected sine waves in the Sine Amplitudes field.
Choose signal amplitudes which have magnitudes above the noise floor of the system and will not saturate the system. For this example there is no noise in the system to consider. However, the controller output (duty cycle of the PWM) is limited to [0 1] and the nominal output of the controller at steady-state is 0.5. To remain within these limits, specify a sine amplitude of 0.1. Specifying a scalar value uses the same amplitude at all four frequencies.
For an asymptotically stable plant, the tuner also injects a step signal to estimate the plant DC gain. Choose an amplitude for this step signal based on the same considerations you used to choose the sine amplitudes. For this example, enter 0.1 in the Step Amplitude field as well.
Specify Design Goals
Finally, specify the target bandwidth for tuning. As noted previously, the target bandwidth is 8000 radians per second. Enter 8000 in the Bandwidth field. The default target phase margin, 60 degrees, corresponds to an overshoot of about 10% or better.
Tune PID Controller and Validate Results
Click Tune to begin the two simulations of the buck converter and tune the PID Controller.
At the conclusion of the tuning procedure, the tuned gains, estimated phase margin, and nominal plant input are displayed in the Frequency Response Based PID Tuner dialog box in the Tuning Results section. Check the estimated phase margin to ensure that it is close to the Target phase margin.

To verify the results, simulate the model using the tuned PID gains. Click Update PID Block to write the tuned gains to the PID Controller block. Then, simulate the model to confirm the PID controller performance.

See Also
PID Controller | PID Controller (2DOF) | Discrete PID Controller | Discrete PID Controller (2DOF)