Augment Block Linearization
This example shows how to augment the linearization of a block with additional time delay dynamics using a block linearization specification function.
Open the Simulink® model.
mdl = 'scdFcnCall';
open_system(mdl)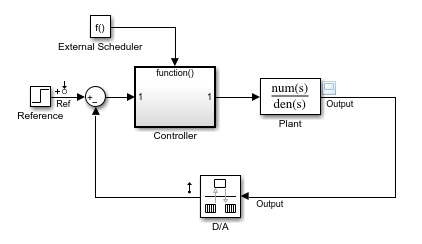
This model includes a continuous-time plant and a discrete-time controller. The D/A block discretizes the plant output with a sample time of 0.1 s. The External Scheduler block triggers the controller to execute with the same period. However, the trigger has an offset of 0.05 s relative to the discretized plant output. For that reason, the controller does not process a change in the reference signal until 0.05 s after the change occurs. This offset introduces a time delay of 0.05 s into the model.
Linearize the closed-loop model at the model operating point without specifying a linearization for the Controller block.
io = getlinio(mdl); sys_nd = linearize(mdl,io);
Check the linearization result by frequency response estimation.
input = frest.Sinestream(sys_nd); sysest = frestimate(mdl,io,input); bode(sys_nd,'g',sysest,'r*',{input.Frequency(1),input.Frequency(end)}) legend('Linearization without delay',... 'Frequency response estimation','Location','southwest')

The exact linearization does not account for the time delay introduced by the controller execution offset. There is a discrepancy in the results between the linearized model and the estimated model, especially at higher frequencies.
Create a function to specify the linearization of the Controller block that includes the time delay. For this example use the linearization specified in scdAddDelayFcn.m.
function sys = scdAddDelayFcn(BlockData) sys = BlockData.BlockLinearization*thiran(0.05,0.1); end
The input to the function, BlockData, is a structure that the software creates automatically each time it linearizes the block. When you specify a block linearization configuration function, the software automatically passes BlockData to the function. The field BlockLinearization contains the current linearization of the block.
This configuration function approximates the time delay as a Thiran filter. The filter indicates a discrete-time approximation of the fractional time delay of 0.5 sampling periods. (The 0.05 s delay has a sample time of 0.1 s).
Specify scdAddDelayFcn as the linearization for the Controller block.
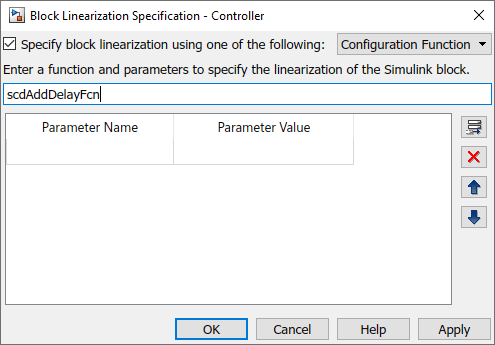
Right-click the Controller block, and select Linear Analysis > Specify Selected Block Linearization.
In the Block Linearization Specification dialog box, select Specify block linearization using one of the following.
In the drop-down list, select
Configuration Function.In the text box, enter the function name
scdAddDelayFcn. This function has no additional parameters, so leave the parameter table blank.Click OK.
Alternatively, you can specify the configuration function programmatically using the following code.
block = 'scdFcnCall/Controller'; set_param(block,'SCDEnableBlockLinearizationSpecification','on') rep = struct('Specification','scdAddDelayFcn',... 'Type','Function',... 'ParameterNames','',... 'ParameterValues',''); set_param(block,'SCDBlockLinearizationSpecification',rep)
Linearize the model using the augmented block linearization.
sys_d = linearize(mdl,io);
Compare the linearization that includes the delay with the estimated frequency response.
bode(sys_d,'b',sys_nd,'g',sysest,'r*',... {input.Frequency(1),input.Frequency(end)}) legend('Linearization with delay','Linearization without delay',... 'Frequency response estimation','Location','southwest')

The linear model obtained using the augmented block linearization now accounts for the time delay. This linear model more closely matches the real frequency response of the model.