Declare Variable-Size MATLAB Function Block Variables
MATLAB Function blocks support variables that change size during simulation if the
Support variable-size array block property is enabled. See Support variable-size arrays. However, only variables
that you specify as variable size can change in size during simulation. Depending on the
scope, you can set variables as variable size by using the MATLAB Function Block
Editor, by using the coder.varsize function, or by inheriting
size variability from the connected block signal. For more information about scope, see Scope.
Output Variables
By default, output variables are not variable size. To specify an output as variable size, use the Symbols pane and the Property Inspector (since R2022a):
Double-click the MATLAB Function block to open the MATLAB Function Block Editor.
In the Function tab, click Edit Data to open the Symbols pane and the Property Inspector.
In the Symbols pane, select the output variable.
In the Property Inspector, in the Properties tab, select the Variable size property.
In the Size property, specify the size as the upper bound. For example, to specify a 2-by-4 matrix as the largest acceptable size, enter
[2 4]. If you do not know the upper bound of the size, useInfas the higher bound to create an unbounded variable-size array. (since R2023b) For more information, see Customize Variable Sizes and Unbounded Variable-Size Signals.
Other Scope Types
Input variables inherit size from their attached signals. Therefore, you do not explicitly define input variables as variable size. Input variables can also be unbounded. For more information on creating variable-size signals, see Variable-Size Signal Basics.
If the variable is not an input or output variable, define the variable by using the
coder.varsize function. See Define Variable-Size Data Explicitly by Using coder.varsize.
Use a Variable-Size Signal in a Filtering Algorithm
This example uses a variable-size vector to store the values of a white noise signal.
The size of the vector can vary at run time because the functions prune the signal values by:
Filtering out signal values that are not unique to within a specified tolerance of each other.
Averaging every two signal values and outputting only the resulting means.
In this model, a Band-Limited White Noise block generates a set of normally distributed random values as the source of a white noise signal. The MATLAB Function block Filter filters out signal values that are not unique to within a specified tolerance of each other. Then, the MATLAB Function block Average outputs the average of a specified number of unique signal values. The Scope blocks display the output from the Filter and Average blocks. Open the model to see the configuration.
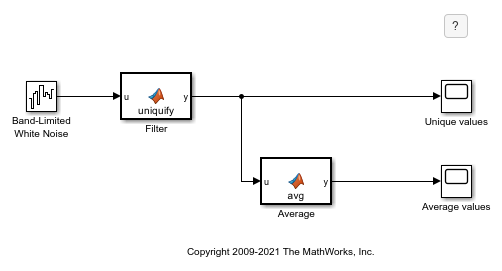
Inspect the Source Signal
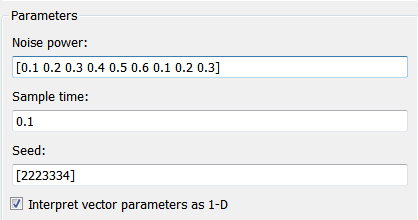
Open the Band-Limited White Noise block to view the properties of the source signal. The size of the Noise power parameter defines the size of the array that holds the signal values. This array is a 1-by-9 vector of double values.
Inspect the Filter MATLAB Function Block
Open Filter to inspect the filtering function. Filter filters out unique signal values that are not within a tolerance of 0.2 of each other. The function calls an external MATLAB® function file, emldemo_uniquetol.m, to filter the signal values. The function passes the 1-by-9 vector of white noise signal values as the first argument and the tolerance value as the second argument.
function y = uniquify(u)
y = emldemo_uniquetol(u,0.2);
Open the MATLAB function file emldemo_uniquetol.m to view the code for the external function, emldemo_uniquetol. emldemo_uniquetol returns the filtered values of A in an output vector B so that abs(B(i) - B(j)) > tol for all i and j.
function B = emldemo_uniquetol(A,tol) %#codegen
A = sort(A); B = A(1); k = 1; for i = 2:length(A) if abs(A(k) - A(i)) > tol B = [B A(i)]; k = i; end end
At each time step, the Band-Limited White Noise block generates a different set of random values for A, and emldemo_uniquetol may produce a different number of output signals in B. Therefore, y must be variable size. In order for y to be variable size, you must enable the Variable size property. In this example, Variable size is enabled for y. In Filter , open the Symbols pane and Property Inspector. In the Function tab, click Edit Data. In the Symbols pane, click y to view the properties in the Property Inspector. For variable-size outputs, you must specify the Size property as the maximum-size upper bound. In the example, Size is [1 9].

Inspect the Average MATLAB Function Block
Average averages the values filtered by Filter by following these conditions:
If the number of signals is greater than
1and divisible by2, thenAverageaverages every consecutive pair of values.If the number of signals is greater than
1but not divisible by2, thenAveragedrops the first value and averages the remaining consecutive pairs.If there is exactly one signal, then
Averagereturns the value unchanged.
Open Average to view the code.
function y = avg(u)
if numel(u) == 1 y = u; else k = numel(u)/2; if k ~= floor(k) u = u(2:numel(u)); end y = emldemo_navg(u,2); end
The avg function calls the external MATLAB function emldemo_navg to calculate the average of every two consecutive signal values.
function B = emldemo_navg(A,n) %#codegen
assert(n>=1 && n<=numel(A));
B = zeros(1,numel(A)/n); k = 1; for i = 1 : numel(A)/n B(i) = mean(A(k + (0:n-1))); k = k + n; end
Both u and y are variable size. You do not need to explicitly define u as variable size, because u is an input. The output y is declared as a variable-size vector because the number of elements varies depending on the size provided by u. Inspect the properties of y to confirm that it is variable size.
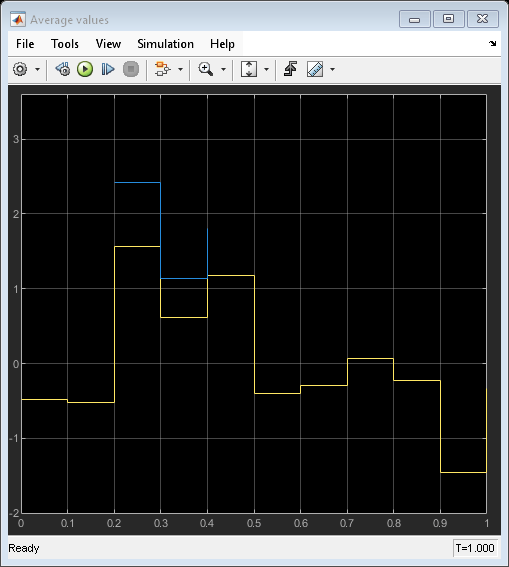
Simulate the Model
Simulate the model to view the results in each Scope block. Filter outputs a variable number of signal values each time it executes.

Average outputs a variable number of signal values each time it executes. The block returns approximately half the number of the unique values.