Model Thermal Effects in a Closed-Loop System
In the Simple Gas Model tutorial, you created a simple open-loop gas model, which
you then modified in the Change Model into Closed-Loop System tutorial into a
closed-loop system. This example shows how to further modify this model by accounting
for the thermal effects in a closed-loop gas system. To open the completed model, in the
MATLAB® Command Window, type ssc_gas_tutorial_step5.
To account for the thermal effects in a closed-loop gas system:
Open the model used in the Change Model into Closed-Loop System tutorial, by typing
ssc_gas_tutorial_step4.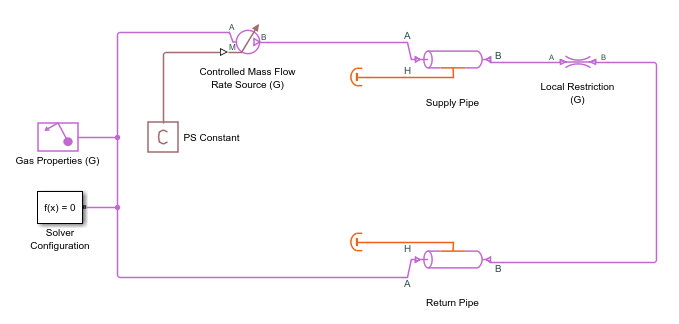
In this closed system, the source is no longer intended to be simply a part of the boundary conditions. Instead, the source represents an idealized compressor that drives the gas flow through this loop. Therefore, open the Controlled Mass Flow Rate Source (G) block dialog box and switch the Power added parameter from
Noneback toIsentropic.Simulate the model and view the simulation results in the Simscape™ Results Explorer.
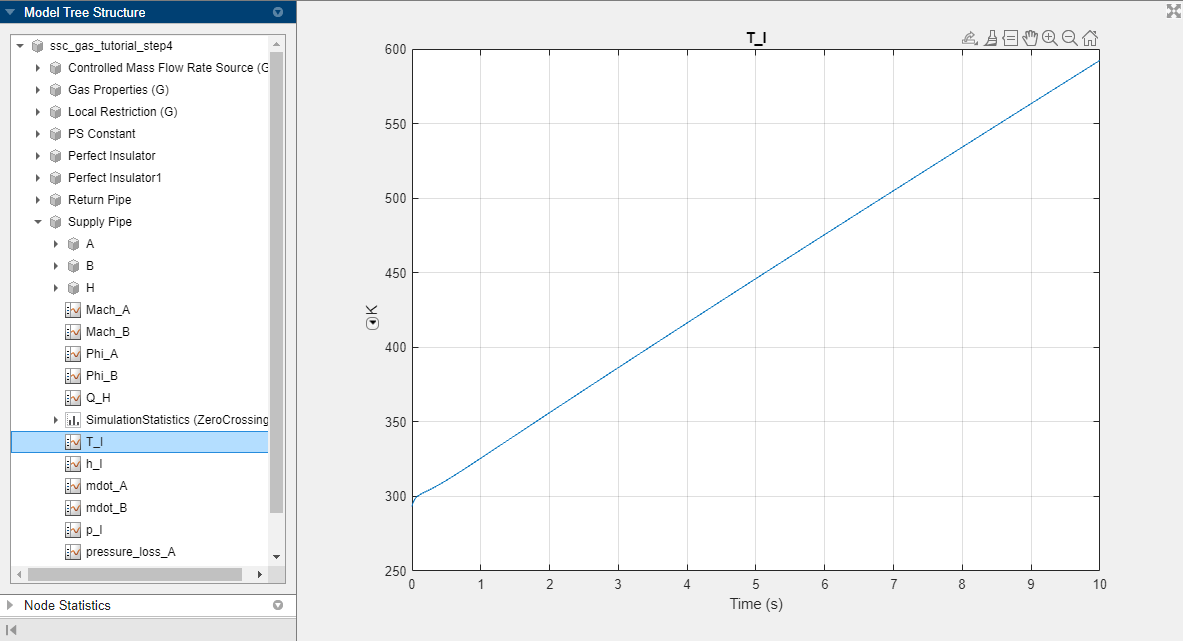
T_Iis the gas volume temperature inside the Supply Pipe block. It keeps rising because the source is doing work and adding energy to the system, but the pipes are insulated so there is no path for any heat to escape the closed system.Assuming that the pipe wall is kept at a constant ambient temperature, replace the Perfect Insulator blocks with a Temperature Source block set to 293.15 K.
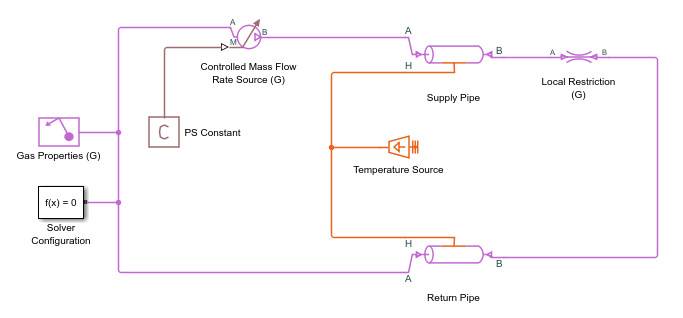
Simulate the model again.
Now,
T_Iof the Supply Pipe block increases and reaches steady state at 308.5 K, andT_Iof the Return Pipe block reaches steady state at 302.1 K.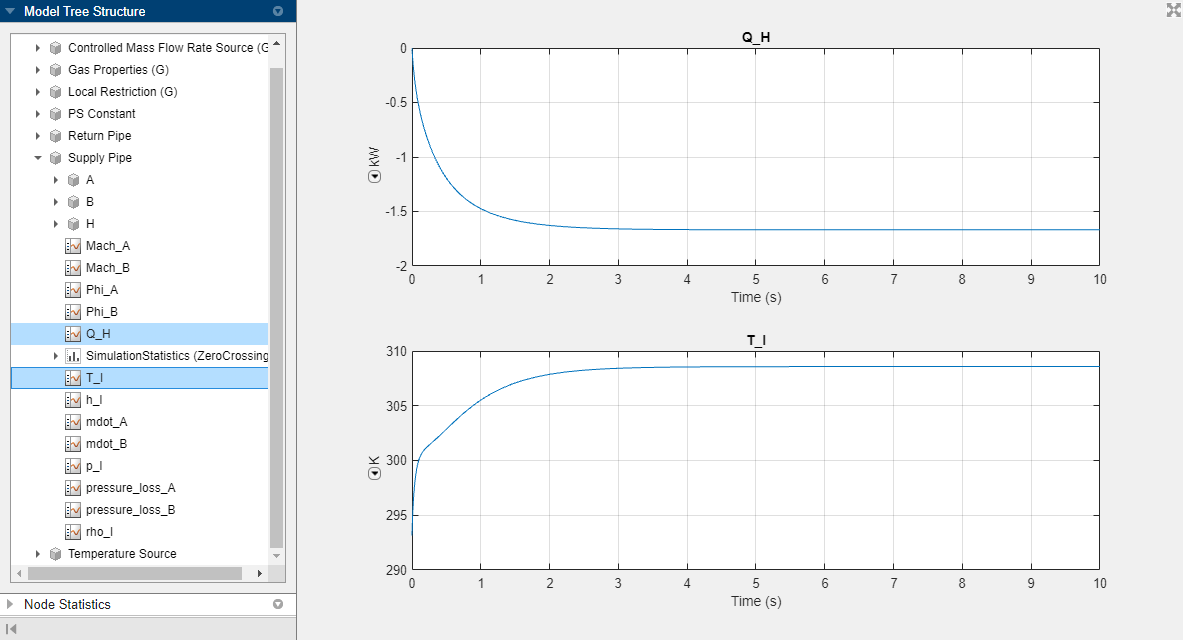
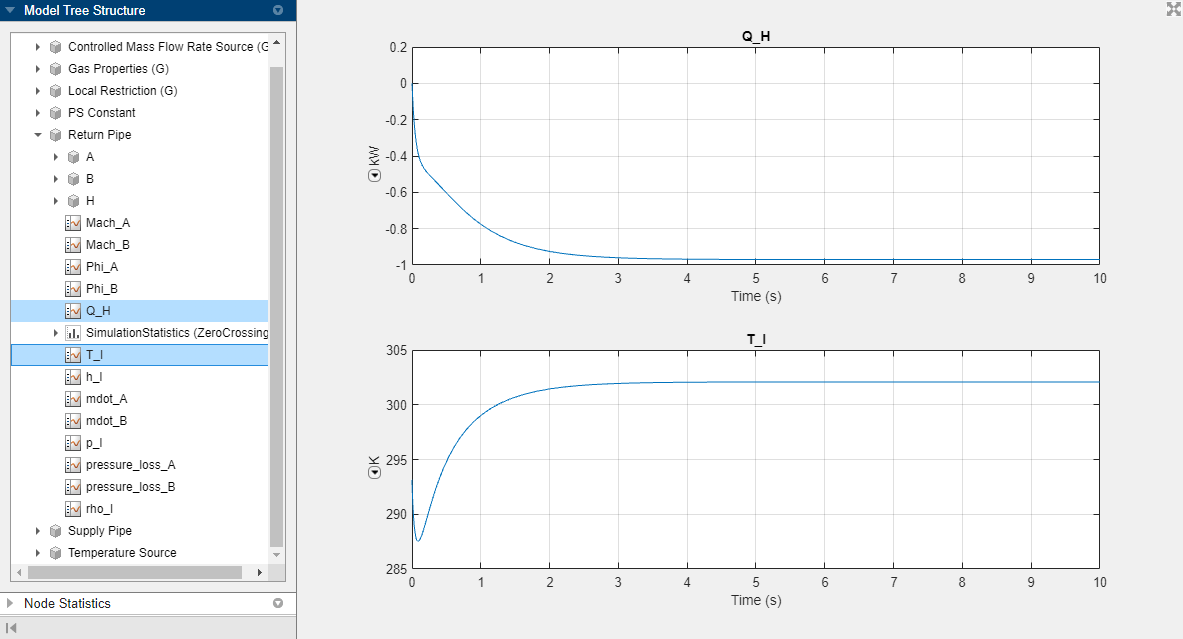
At steady state, the amount of heat leaving the pipe,
Q_H, is about 1.6 kW for the Supply Pipe block and about 1 kW for the Return Pipe block. If you look at the simulation data for the Controlled Mass Flow Rate Source (G) block, you can see that the power added to the flow by the source is about 2.6 kW, which balances out the heat leaving the pipes.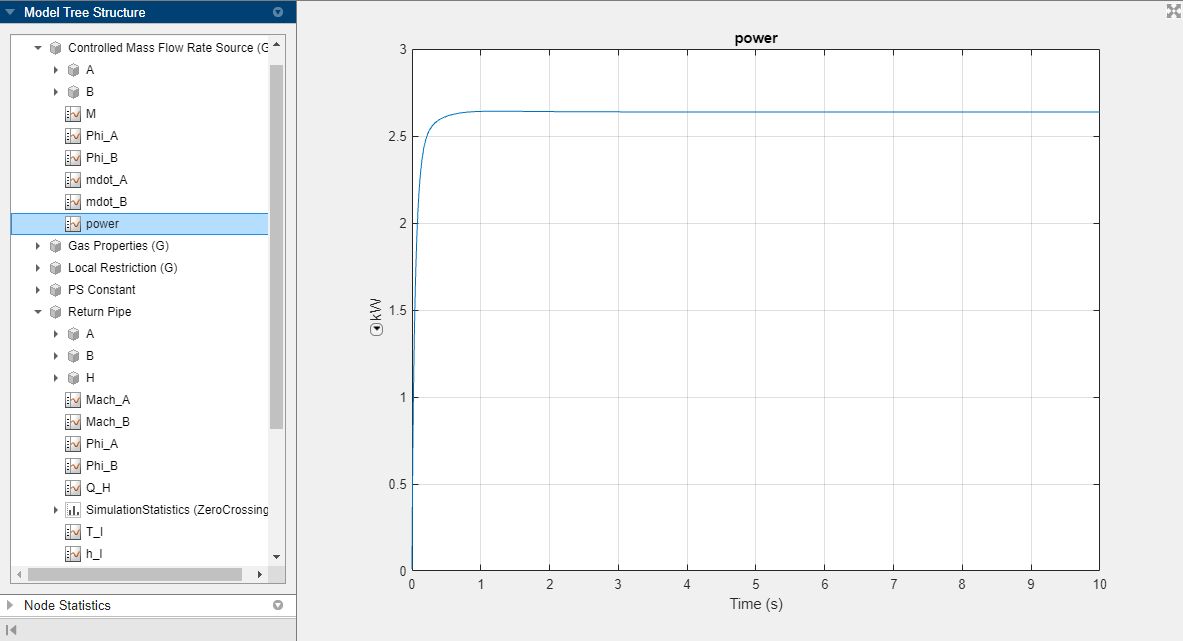
All blocks with a finite gas volume have a thermal port that let you model the heat exchange between the gas volume and the environment outside of the gas system. In a more detailed model, you can connect additional thermal blocks, for example, to model the effects of conduction and thermal mass of the pipe wall, or convection with the ambient air.