Preprocess Measured Data for PA Model Identification
This example shows you how to:
Import the PA characterization data: This example uses two different input/output complex modulated waveforms measured in different conditions to extract and verify the quality of the PA model.
Visualize the characterization data in different domains to make it suitable for fitting a memory polynomial PA model.
PA data manipulation: The PA measured data might need manipulation, such as adjusting the input/output timing alignment. In this case, the data is filtered to reduce the characterization bandwidth.
Evaluate different data processing techniques to compensate for undesired effects impacting the measured data such as frequency, phase, and DC offsets.
Read PA Input/Output Characterization Data
The K18m_PA_Data.mat included with this example contains the PA input and output waveforms measured using Rohde & Schwarz vector signal generator R&S®SMW200A in conjunction with the vector signal analyzer R&S®FSW. The file includes four different complex waveforms, measured at 2.6 GHz, with a sample time of 1.6276 ns.
The four waveforms provide two different sets of input/output characterization data. The first set (reference) is measured using a standard compliant 5G waveform. The second set is measured using a predistorted waveform generated by the Rohde & Schwarz setup. This excitation waveform is created using the iterative direct digital predistortion (DPD) approach, and provides a measure of the PA linearized performance that can be achieved in the field. In this example, you will use one of these two sets of waveforms to extract the PA model, and the second set to verify the quality of the fitting in the model.
iq_in— Original PA input data (reference)iq_out— Original PA output data (no DPD active)iq_in_dpd— Predistorted PA input signal (iterative direct DPD)iq_out_dpd— PA output signal using pre-distorted input signal
Load the data file.
load('K18m_PA_Data.mat');
Plot Spectrum of PA Characterization Data
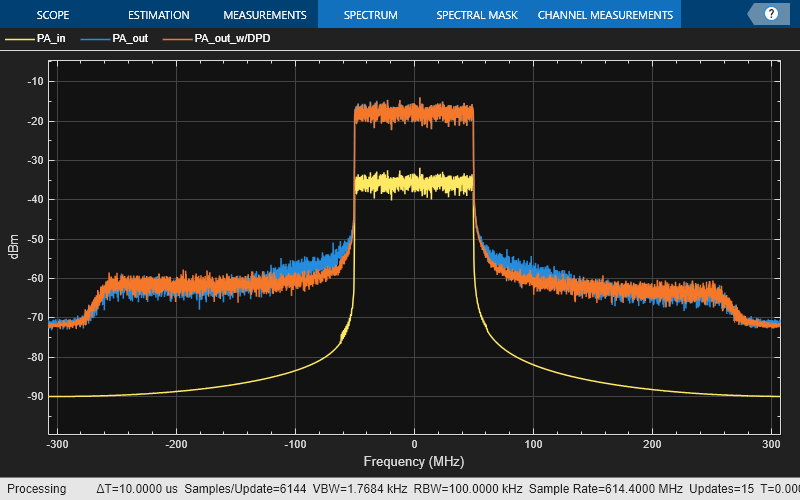
Plot the spectrum of the data used to characterize the PA. You can see the effects of the filtering introduced by the measurement setup at the edges of the signal.
SpectAnalyzer = spectrumAnalyzer; SpectAnalyzer.SampleRate = fs; SpectAnalyzer.ShowLegend = true; SpectAnalyzer.ReferenceLoad = 50; SpectAnalyzer.RBWSource= "Property"; SpectAnalyzer.RBW = 1e5; SpectAnalyzer([iq_in, iq_out, iq_out_dpd]); SpectAnalyzer.ChannelNames = {'PA_in','PA_out','PA_out_w/DPD'};
Apply Resampling Filter to Remove Filter Effects
Apply a digital multirate FIR filter to resample the data and remove the effects of filtering introduced by the measurement setup. This step is recommended to improve the fit quality of the PA model.
Set the filter parameters starting with the number of filter taps, interpolation and decimation factors, and overall length of the filter delay in number of samples.
filtLength = 48*2; I = 6; D = 8; N = ceil(filtLength*((I/D)+1));
Compute the oversampling factor and sample time of the resampled waveforms.
ovs = I/D; Tstep = 1/fs/ovs;
Create a filter object using the parameters.
FIR_bw = designMultirateFIR(I,D,filtLength,'SystemObject',true);
Apply the filter to all four characterization waveforms.
inDataPA1 = FIR_bw(iq_in); inDataPA2 = FIR_bw(iq_in_dpd); outDataPA1 = FIR_bw(iq_out); outDataPA2 = FIR_bw(iq_out_dpd);
Remove the filter transient at the beginning of all the waveforms and store the data in two matrices: one for the input waveforms, and one for the output waveforms. The first column in both matrices represents the original data, and the second column represents the data measured using the iterative direct DPD approach.
in(:,1) = inDataPA1(N:end); in(:,2) = inDataPA2(N:end); out(:,1) = outDataPA1(N:end); out(:,2) = outDataPA2(N:end); numDataPts = length(in(:,1));
Plot PA Waveforms in Time and Frequency Domain
Visualize the input and output characterization data with and without iterative direct DPD.
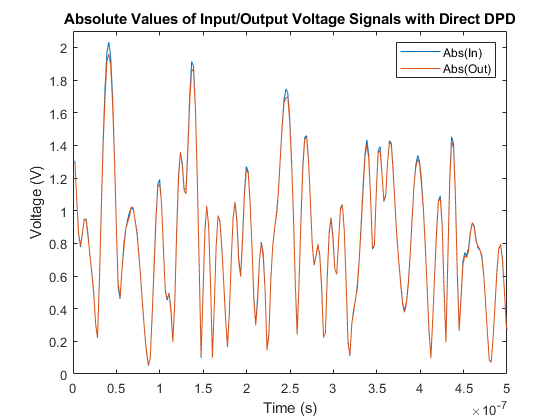
In these figures, you plot the first 500 ns of data. The data is well aligned in time, and the effects of nonlinearity are barely visible in the peaks of the output signals. For direct comparison, multiply the data by the PA gain.
g = 10^(g0/20); for i = 1:2 figure; plot((1:numDataPts)*Tstep, abs(in(:,i))*g, ... (1:numDataPts)*Tstep, abs(out(:,i))) legend('Abs(In)','Abs(Out)','Location','northeast') xlabel('Time (s)') xlim([0 0.5e-6]); ylim([0 2.1]); ylabel('Voltage (V)') if i==1 title('Absolute Values of Original Input/Output Voltage Signals'); else title('Absolute Values of Input/Output Voltage Signals with Direct DPD'); end end
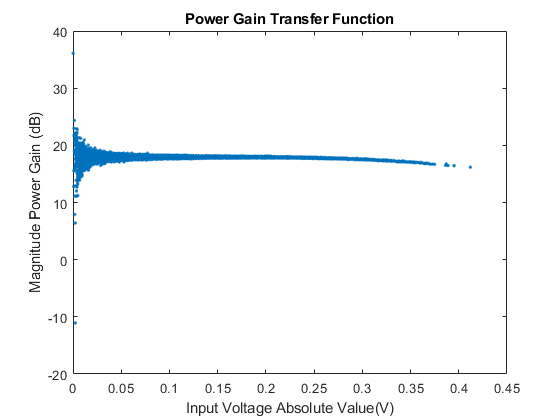
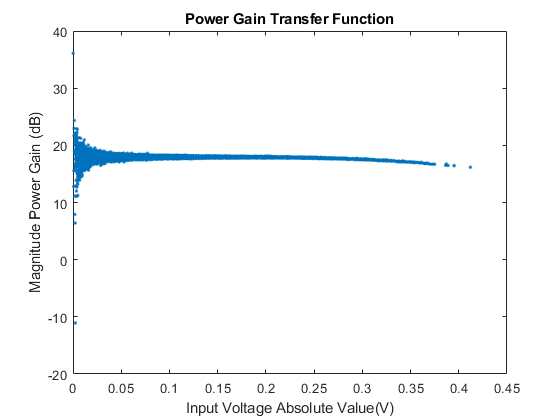
Plot the power gain transfer function. The plot helps you visualize memory effects as well as the PA nonlinearity. The power transfer function of a perfectly linear device without any memory effects is a straight line, so any deviation from the line due to nonidealities. From the comparison of the two plots, you can verify that the characterization data measured with the iterative direct DPD approach has a larger dynamic range.
for i = 1:2 figure; TransferPA = abs(out(:,i)./in(:,i)); plot(abs(in(:,i)),20*log10(TransferPA),'.'); xlabel('Input Voltage Absolute Value(V)') ylabel('Magnitude Power Gain (dB)') if i==1 title('Power Gain Transfer Function') else title('Power Gain Transfer Function with Direct DPD') end end
Plot the power spectrum of the output signal and verify that the resampling filter delivers the desired results. You can use the characterization data to identify a memory polynomial model. With the given measurement bandwidth, you can capture the spectral regrowth up to the fifth order of nonlinearity.
SpectAnalyzer = spectrumAnalyzer; SpectAnalyzer.SampleRate = fs*ovs; SpectAnalyzer.ShowLegend = true; SpectAnalyzer.ReferenceLoad = 50; SpectAnalyzer.RBWSource= "Property"; SpectAnalyzer.RBW = 1e5; SpectAnalyzer(out(:,1:2)); SpectAnalyzer.ChannelNames = {'PA_out','PA_out_w/DPD'};

Add Impairments to Measured Waveform
These waveforms have been generated and measured under conditions where both the signal generator and measurement equipment are synchronized with one another, and no timing or frequency offsets need to be considered. A PA under test could be part of a complex chip or the measurement could have been executed with a SoC device. When this occurs, effects such as LO frequency offset, DC offset, and timing offset need to be isolated, characterized and calibrated out or "de-embedded" from the waveforms that will be used in the PA model identification process.
This example adds specific impairments to the PA measurement waveforms that were already imported and shows how to identify and remove these impairments using different signal processing algorithms.
First, create a new set of output waveforms where you add the timing impairments.
outImperfect = out(:,1); time = Tstep*(0:numDataPts-1).';
Add synthetic time, carrier frequency, and DC offset to the PA output signal. Specify the value of the impairments.
Time_offset = 500; %number of samples LO_offset = 1e3; %Hz DC_offset = 0.1 - 0.2i; %V
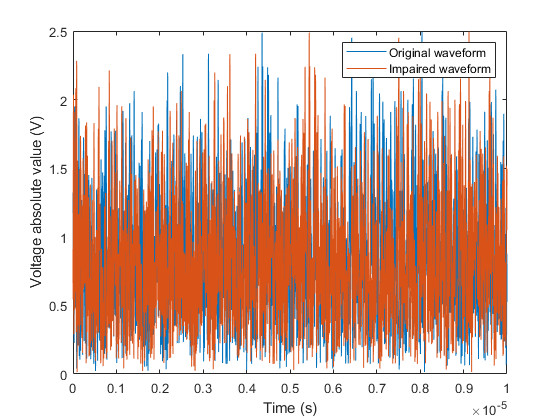
Add the timing offset and visualize the impaired waveform in comparison to the original waveform.
outImperfect(Time_offset+1:numDataPts) = out(1:numDataPts-Time_offset); outImperfect(1:Time_offset,1) = out(numDataPts-Time_offset+1:numDataPts); figure; plot(time, abs(out(:,1)), time, abs(outImperfect)); xlim([0 10e-6]); xlabel('Time (s)') ylabel('Voltage absolute value (V)') legend({'Original waveform', 'Impaired waveform'})

Then add and visualize the frequency offset by plotting 50 samples in the middle of the waveforms in the complex plane.
outImperfect = outImperfect.*exp(-1j*2*pi*LO_offset*time); m = round(numDataPts/2); figure; plot(out(numDataPts-Time_offset+1-m:numDataPts-Time_offset-m+50,1)); hold on; plot(outImperfect(m:m+50)); xlabel('Voltage I component (V)') ylabel('Voltage Q component (V)') legend({'Original waveform', 'Impaired waveform'})

Then add and visualize the impact of the DC offset.
outImperfect = outImperfect + DC_offset; figure; plot(time, abs(out(:,1)), time, abs(outImperfect)); xlim([0 10e-6]); xlabel('Time (s)') ylabel('Voltage absolute value (V)') legend({'Original waveform', 'Impaired waveform'})
Determine Time Delay Between Input and Output Measurement Waveform
Apply correlation to programmatically determine the time delay in samples between the input and output.
x=xcorr(outImperfect,in(:,1)); % % Find value and index of maximum value of cross-correlation amplitude % [m,d]=max(x); % % As the length of the correlation vector x is equal to 2*numDataPts-1 % need to apply an offset to determine the actual delay: % Time_delay=d-numDataPts; disp(['Applied Timing offset = ' num2str(Time_offset) ' samples']); disp(['Estimated Timing offset = ' num2str(Time_delay) ' samples']);
Applied Timing offset = 500 samples Estimated Timing offset = 500 samples
Verify that the computed time delay value is correct, and remove the delay from the imperfect signal.
figure; plot(abs(out(1:end,1))); hold on; plot(abs(outImperfect(Time_delay+1:end))); xlim([0 100]); xlabel('Sample number') ylabel('Voltage absolute value (V)') legend({'Original delayed waveform', 'Impaired waveform'}) outCorrected = [outImperfect(Time_delay+1:end)];
Determine DC offset From PA Output Signal
Use the mean operator to compute the DC level, and compare it with the value originally applied. Remove the DC offset from the impaired signal.
DC_level = mean(outImperfect); disp(['Applied DC offset = ' num2str(DC_offset) ' V']); disp(['Estimated DC offset = ' num2str(DC_level) ' V']); outCorrected = outCorrected - DC_level;
Applied DC offset = 0.1-0.2i V Estimated DC offset = 0.1031-0.2003i V
Determine Frequency Offset Using Cyclic Prefix Information
Use the 5G signal characteristics to first determine the separation between cyclic prefix sequences. Use this separation to determine a time-dependent frequency offset that can be approximated as a frequency offset, as such this algorithm is iterative and it loops along the signal duration.
First, compute the signal autocorrelation to identify occurrences of the cyclic prefix.
x = xcorr(outCorrected); [~, cp_rep_idx] = findpeaks(abs(x),'SortStr','descend',... 'MinPeakHeight',1e4,'MinPeakDistance',1e3); cp_delay = abs(cp_rep_idx(2)-cp_rep_idx(1));
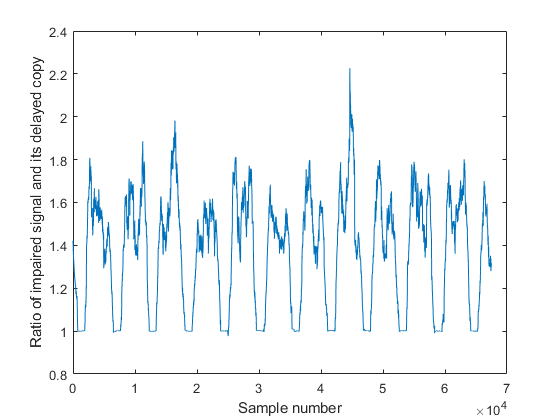
Identify where the cyclic prefix occurs in the signal. By dividing the signal by a delayed copy of itself, you can identify the cyclic prefix where the signal is close to 1. Then apply averaging techniques to smooth the signal and more easily identify the location of the cyclic prefix. You can expect to find 12 cyclic prefix repetitions in this example.
cp_iden = abs(outCorrected(1:end-cp_delay)./outCorrected(1+cp_delay:end)); mcp = movmean(cp_iden,800); figure; plot(mcp); xlabel('Sample number') ylabel('Ratio of impaired signal and its delayed copy')

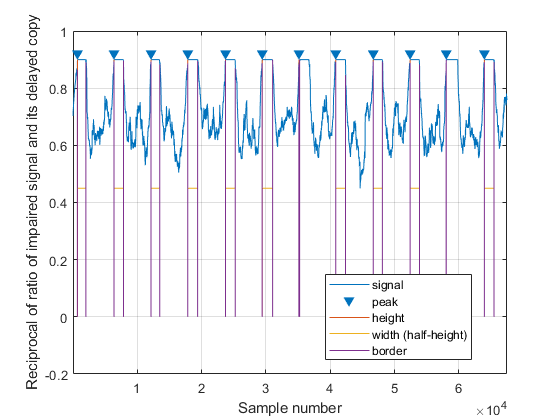
Use the findpeaks function to determine where the cyclic prefix occurs and its duration.
findpeaks(min(1./mcp,0.9),'Annotate','extents','MinPeakHeight',0.7,... 'MinPeakDistance',5e3,'WidthReference','halfheight'); [~,cp,w] = findpeaks(min(1./mcp,0.9),'MinPeakHeight',0.7,... 'MinPeakDistance',5e3,'WidthReference','halfheight'); xlabel('Sample number') ylabel('Reciprocal of ratio of impaired signal and its delayed copy')

Loop in the frequency search range for determining the frequency offset that minimizes the difference of the first cyclic prefix occurrence that you have identified.
cp_duration = round(mean(w)/3); Freq_offset = []; w = 1; norm_out = 0; Npts = 500; searchRange = linspace(500, 2e3, Npts); %Hz for m1 = 1:Npts w(m1)=2*pi*searchRange(m1); norm_out(m1) = std(outCorrected(cp(1):cp(1)+cp_duration)... .*exp(1j*w(m1).*time(cp(1):cp(1)+cp_duration))-... outCorrected(cp(1)+cp_delay:cp(1)+cp_delay+cp_duration)... .*exp(1j*w(m1).*time(cp(1)+cp_delay:cp(1)+cp_delay+cp_duration))); if m1 > 2 if (norm_out(m1)>norm_out(m1-1) && norm_out(m1-1)<norm_out(m1-2)),... Freq_offset=w(m1-1)/2/pi; break end end end disp(['Applied Frequency offset = ' num2str(LO_offset) 'Hz']); disp(['Estimated Frequency offset = ' num2str(Freq_offset) 'Hz']);
Applied Frequency offset = 1000Hz Estimated Frequency offset = 1014.0281Hz
Remove the computed frequency offset and compare the resulting waveform in the complex domain against the original waveform before applying any impairment.
outCorrected = outCorrected.*exp(1j*2*pi*Freq_offset.*time(1:length(outCorrected))); figure; m = round(numDataPts/2); plot(out(m:m+50,1)); hold on; plot(outCorrected(m:m+50)); xlabel('Voltage I component (V)') ylabel('Voltage Q component (V)') legend({'Original waveform', 'Corrected waveform'})
