Power Spectral Density Estimates Using FFT
This example shows how to obtain equivalent nonparametric power spectral density (PSD) estimates using the periodogram and fft functions. The different cases show you how to properly scale the output of fft for even-length inputs, for normalized frequencies and frequencies in hertz, and for one- and two-sided PSD estimates. All cases use a rectangular window.
This example focuses on stationary signals whose frequency content is constant in time. For nonstationary signals with time-dependent frequency content, the short-time Fourier transform is a better analysis tool. For more information, see Spectrogram Computation with Signal Processing Toolbox.
Even-Length Input with Sample Rate
Obtain the periodogram for an even-length signal sampled at 1 kHz using both fft and periodogram. Compare the results.
Create a signal consisting of a 100 Hz sine wave in N(0,1) additive noise. The sampling frequency is 1 kHz. The signal length is 1000 samples.
fs = 1000; t = 0:1/fs:1-1/fs; x = cos(2*pi*100*t) + randn(size(t));
Obtain the periodogram using fft. The signal is real-valued and has even length. Because the signal is real-valued, you only need power estimates for the positive or negative frequencies. In order to conserve the total power, multiply all frequencies that occur in both sets — the positive and negative frequencies — by a factor of 2. Zero frequency (DC) and the Nyquist frequency do not occur twice. Plot the result.
N = length(x); xdft = fft(x); xdft = xdft(1:N/2+1); psdx = (1/(fs*N)) * abs(xdft).^2; psdx(2:end-1) = 2*psdx(2:end-1); freq = 0:fs/length(x):fs/2; plot(freq,pow2db(psdx)) grid on title("Periodogram Using FFT") xlabel("Frequency (Hz)") ylabel("Power/Frequency (dB/Hz)")

Compute and plot the periodogram using periodogram. Show that the two results are identical.
periodogram(x,rectwin(N),N,fs)

mxerr = max(psdx'-periodogram(x,rectwin(N),N,fs))
mxerr = 3.4694e-18
Input with Normalized Frequency
Use fft to produce a periodogram for an input using normalized frequency. Create a signal consisting of a sine wave in N(0,1) additive noise. The sine wave has an angular frequency of rad/sample.
N = 1000; n = 0:N-1; x = cos(pi/4*n) + randn(size(n));
Obtain the periodogram using fft. The signal is real-valued and has even length. Because the signal is real-valued, you only need power estimates for the positive or negative frequencies. In order to conserve the total power, multiply all frequencies that occur in both sets — the positive and negative frequencies — by a factor of 2. Zero frequency (DC) and the Nyquist frequency do not occur twice. Plot the result.
xdft = fft(x); xdft = xdft(1:N/2+1); psdx = (1/(2*pi*N)) * abs(xdft).^2; psdx(2:end-1) = 2*psdx(2:end-1); freq = 0:2*pi/N:pi; plot(freq/pi,pow2db(psdx)) grid on title("Periodogram Using FFT") xlabel("Normalized Frequency (\times\pi rad/sample)") ylabel("Power/Frequency (dB/(rad/sample))")
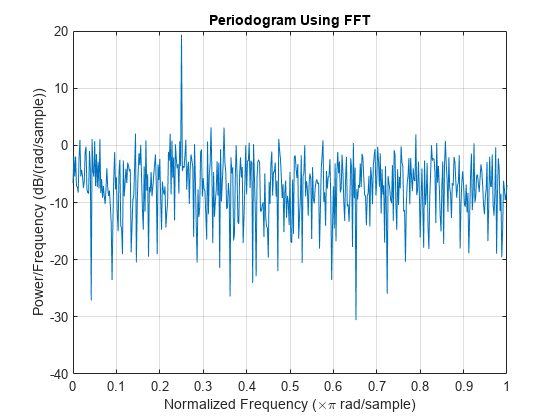
Compute and plot the periodogram using periodogram. Show that the two results are identical.
periodogram(x,rectwin(N),N)

mxerr = max(psdx'-periodogram(x,rectwin(N),N))
mxerr = 4.4409e-16
Complex-Valued Input with Normalized Frequency
Use fft to produce a periodogram for a complex-valued input with normalized frequency. The signal is a complex exponential with an angular frequency of rad/sample in complex-valued N(0,1) noise.
N = 1000; n = 0:N-1; x = exp(1j*pi/4*n) + [1 1j]*randn(2,N)/sqrt(2);
Use fft to obtain the periodogram. Because the input is complex-valued, obtain the periodogram from rad/sample. Plot the result.
xdft = fft(x); psdx = (1/(2*pi*N)) * abs(xdft).^2; freq = 0:2*pi/N:2*pi-2*pi/N; plot(freq/pi,pow2db(psdx)) grid on title("Periodogram Using FFT") xlabel("Normalized Frequency (\times\pi rad/sample)") ylabel("Power/Frequency (dB/(rad/sample))")

Use periodogram to obtain and plot the periodogram. Compare the PSD estimates.
periodogram(x,rectwin(N),N,"twosided")
mxerr = max(psdx'-periodogram(x,rectwin(N),N,"twosided"))mxerr = 2.2204e-16
See Also
Apps
Functions
fft|periodogram|pspectrum