Find a Signal in a Measurement
You receive some data and would like to know if it matches a longer stream you have measured. Cross-correlation allows you to make that determination, even when the data are corrupted by noise.
Load into the workspace a recording of a ring spinning on a tabletop. Crop a one-second fragment and listen to it.
load('Ring.mat') Time = 0:1/Fs:(length(y)-1)/Fs; m = min(y); M = max(y); Full_sig = double(y); timeA = 7; timeB = 8; snip = timeA*Fs:timeB*Fs; Fragment = Full_sig(snip); % To hear, type soundsc(Fragment,Fs)
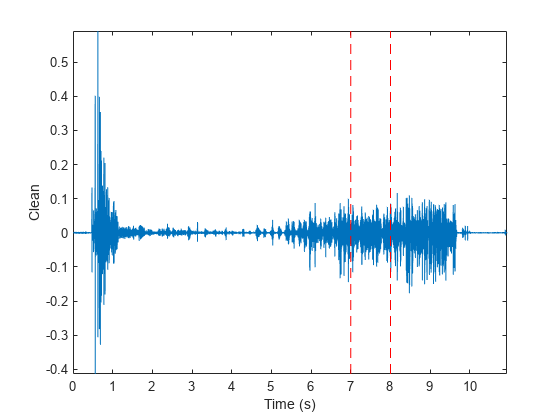
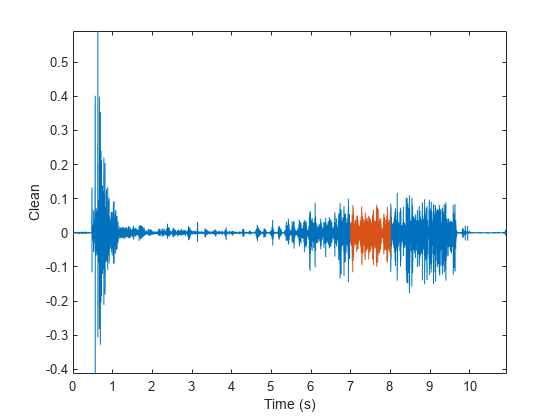
Plot the signal and the fragment. Highlight the fragment endpoints for reference.
plot(Time,Full_sig,[timeA timeB;timeA timeB],[m m;M M],'r--') xlabel('Time (s)') ylabel('Clean') axis tight
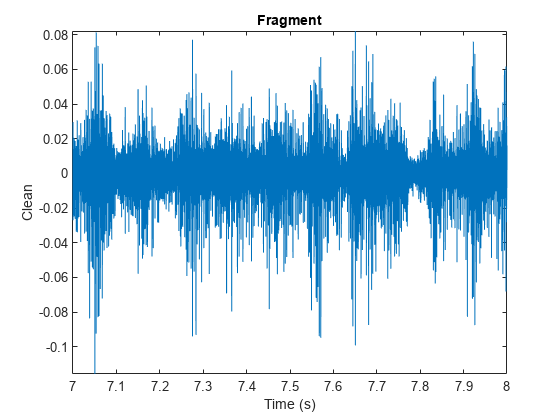
plot(snip/Fs,Fragment) xlabel('Time (s)') ylabel('Clean') title('Fragment') axis tight
Compute and plot the cross-correlation of the full signal and the fragment.
[xCorr,lags] = xcorr(Full_sig,Fragment); plot(lags/Fs,xCorr) grid xlabel('Lags (s)') ylabel('Clean') axis tight
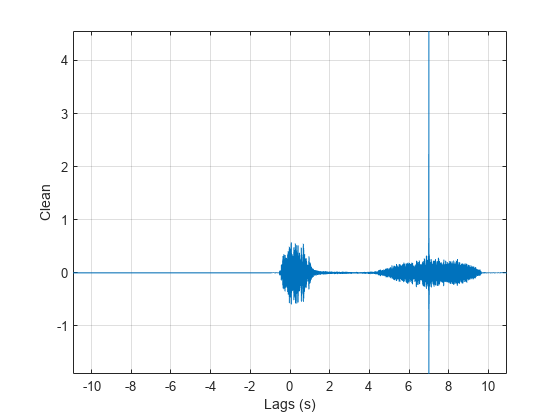
The lag at which the cross-correlation is greatest is the time delay between the signals' starting points. Replot the signal and overlay the fragment.
[~,I] = max(abs(xCorr)); maxt = lags(I); Trial = NaN(size(Full_sig)); Trial(maxt+1:maxt+length(Fragment)) = Fragment; plot(Time,Full_sig,Time,Trial) xlabel('Time (s)') ylabel('Clean') axis tight
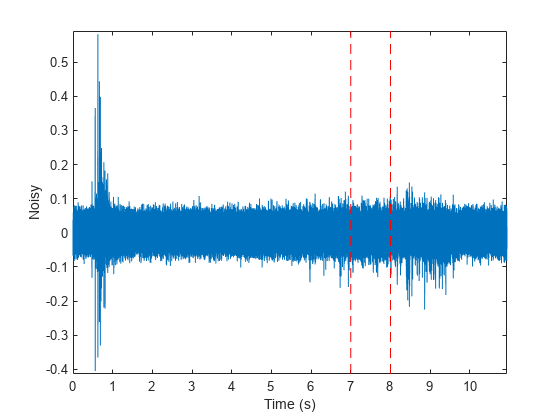
Repeat the procedure, but add noise separately to signal and fragment. The sound cannot be picked out from the noise.
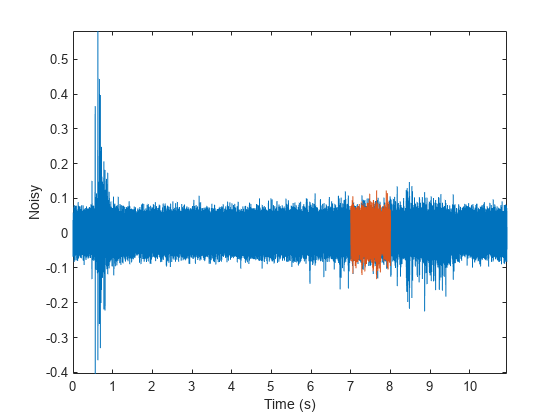
NoiseAmp = 0.2*max(abs(Fragment)); Fragment = Fragment+NoiseAmp*randn(size(Fragment)); Full_sig = Full_sig+NoiseAmp*randn(size(Full_sig)); % To hear, type soundsc(Fragment,Fs) plot(Time,Full_sig,[timeA timeB;timeA timeB],[m m;M M],'r--') xlabel('Time (s)') ylabel('Noisy') axis tight
The procedure finds the missing fragment despite the high noise level.
[xCorr,lags] = xcorr(Full_sig,Fragment); plot(lags/Fs,xCorr) grid xlabel('Lags (s)') ylabel('Noisy') axis tight

[~,I] = max(abs(xCorr)); maxt = lags(I); Trial = NaN(size(Full_sig)); Trial(maxt+1:maxt+length(Fragment)) = Fragment; figure plot(Time,Full_sig,Time,Trial) xlabel('Time (s)') ylabel('Noisy') axis tight