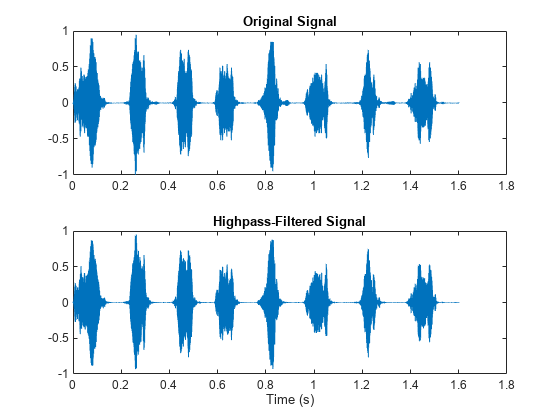
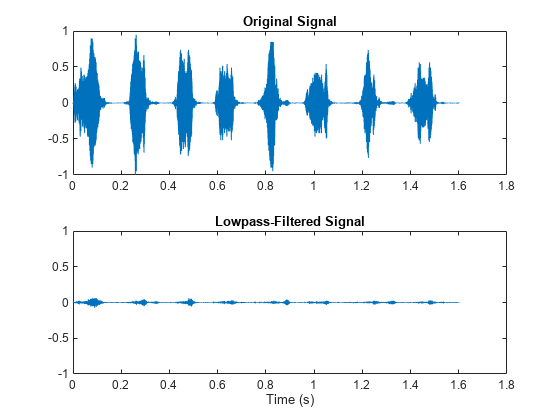
sosfilt
Second-order (biquadratic) IIR digital filtering
Description
y = sosfilt(sos,x)sos to the input signal
x.
If
xis a matrix, then the function operates along the first dimension and returns the filtered data for each column.If
xis a multidimensional array, then the function operates along the first array dimension with size greater than 1.
Examples
Input Arguments
Output Arguments
References
[1] Bank, Balázs. "Converting Infinite Impulse Response Filters to Parallel Form". IEEE Signal Processing Magazine. Vol. 35, Number 3, May 2018, pp. 124-130.
[2] Orfanidis, Sophocles J. Introduction to Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1996.
Extended Capabilities
Version History
Introduced before R2006a
See Also
filter | medfilt1 | sgolayfilt