polystab

Stabilize polynomial

Syntax

b = polystab(a)

Description

b = polystab(a) stabilizes a polynomial of coefficient vector a with respect to the unit circle, reflects roots with magnitudes greater than 1 inside the unit circle, and returns a stabilized polynomial with a coefficient vector b.

Examples

Convert Linear-Phase Filter to Minimum-Phase

Use the window method to design a 25th-order FIR filter with normalized cutoff frequency $$0.4\pi$$ rad/sample. Verify that it has linear phase but not minimum phase.

h = fir1(25,0.4);

h_linphase = islinphase(h)

h_linphase = logical
   1

h_minphase = isminphase(h)

h_minphase = logical
   0

Use polystab to convert the linear-phase filter into a minimum-phase filter. Verify that it has linear phase but not minimum phase.

hmin0 = polystab(h);
hmin = hmin0/norm(hmin0)*norm(h);

hmin_linphase = islinphase(hmin)

hmin_linphase = logical
   0

hmin_minphase = isminphase(hmin)

hmin_minphase = logical
   1

Plot the phase responses of the filters.

phasez(h,1)
hold on
phasez(hmin,1)
hold off
legend("h","hmin")

Verify that the two filters have identical magnitude responses.

[hMag,hW] = freqz(h,1);
[hminMag,hminW] = freqz(hmin,1);

plot(hW,mag2db(abs(hMag)),".-")
hold on
plot(hminW,mag2db(abs(hminMag)))
hold off
grid on
xlabel('Normalized Frequency (\times\pi rad/sample)')
ylabel('Magnitude (dB)')
legend("h","hmin")

Input Arguments

a — Input polynomial coefficients

vector

Input polynomial coefficients, specified as a vector. Each element (a₁, a₂, …, a_m+1) represents the polynomial coefficients, typically in the z-domain:

$$A(z)=a_1+a_2{z}^{-1}\cdots +a_m{z}^{-\left(m-1\right)}+a_{m+1}{z}^{-m}$$

Data Types: single | double
Complex Number Support: Yes

Output Arguments

b — Stabilized polynomial coefficients

row vector

Stabilized polynomial coefficients, returned as a row vector.

Algorithms

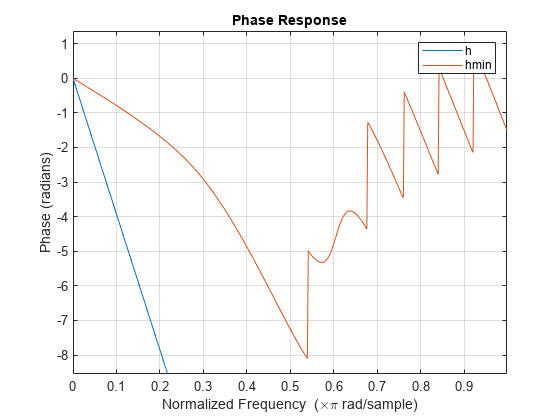
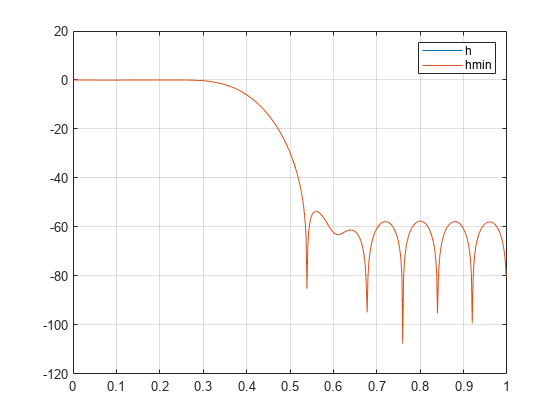
The polystab function finds the roots of the polynomial, maps the roots found outside the unit circle, and relocates them to the inside of the unit circle:

v = roots(a);
vs = 0.5*(sign(abs(v)-1)+1);
v = (1-vs).*v + vs./conj(v);
b = a(1)*poly(v);

Version History

Introduced before R2006a