lpc
Linear prediction filter coefficients
Syntax
Description
[
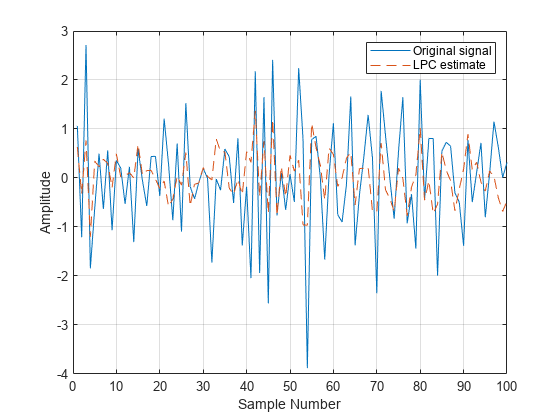
finds the coefficients of a a,g] = lpc(x,p)pth-order linear predictor, an FIR filter
that predicts the current value of the real-valued time series x based
on past samples. The function also returns g, the variance of the
prediction error. If x is a matrix, the function treats each column as
an independent channel.
Examples
Input Arguments
Output Arguments
More About
Algorithms
lpc determines the coefficients of a forward linear predictor by
minimizing the prediction error in the least squares sense. It has applications in filter
design and speech coding.
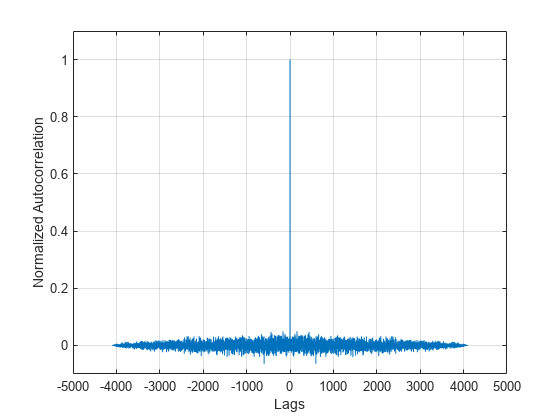
lpc uses the autocorrelation method of autoregressive (AR) modeling
to find the filter coefficients. The generated filter might not model the process exactly,
even if the data sequence is truly an AR process of the correct order, because the
autocorrelation method implicitly windows the data. In other words, the method assumes that
signal samples beyond the length of x are 0.
lpc computes the least-squares solution to Xa = b, where
and m is the length of x. Solving the least-squares problem using the normal equations leads to the Yule-Walker equations
where r =
[r(1) r(2) ... r(p+1)]
is an autocorrelation estimate for x computed using xcorr. The
Levinson-Durbin algorithm (see levinson) solves the Yule-Walker equations in O(p2) flops.
References
[1] Jackson, L. B. Digital Filters and Signal Processing. 2nd Edition. Boston: Kluwer Academic Publishers, 1989, pp. 255–257.