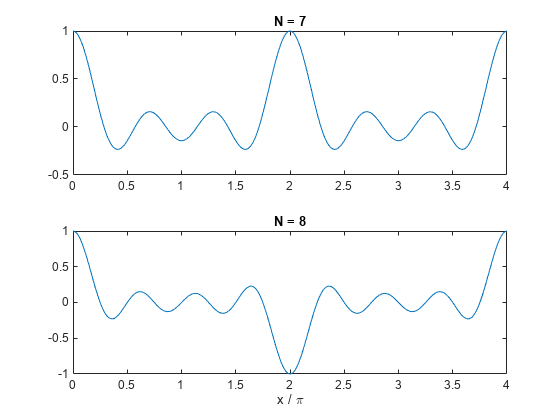
The Dirichlet Function
The function diric computes the Dirichlet function, sometimes called the periodic sinc or aliased sinc function, for an input vector or matrix x. The Dirichlet function is defined by
where is a user-specified positive integer. For odd, the Dirichlet function has a period of ; for even, its period is . The magnitude of this function is times the magnitude of the discrete-time Fourier transform of the -point rectangular window.
To plot the Dirichlet function between 0 and for and , use
x = linspace(0,4*pi,300); subplot(2,1,1) plot(x/pi,diric(x,7)) title('N = 7') subplot(2,1,2) plot(x/pi,diric(x,8)) title('N = 8') xlabel('x / \pi')