Waveform Segmentation Using Deep Learning
This example shows how to segment human electrocardiogram (ECG) signals using recurrent deep learning networks and time-frequency analysis.
Introduction
The electrical activity in the human heart can be measured as a sequence of amplitudes away from a baseline signal. For a single normal heartbeat cycle, the ECG signal can be divided into the following beat morphologies [1]:
P wave — A small deflection before the QRS complex representing atrial depolarization
QRS complex — Largest-amplitude portion of the heartbeat
T wave — A small deflection after the QRS complex representing ventricular repolarization
The segmentation of these regions of ECG waveforms can provide the basis for measurements useful for assessing the overall health of the human heart and the presence of abnormalities [2]. Manually annotating each region of the ECG signal can be a tedious and time-consuming task. Signal processing and deep learning methods potentially can help streamline and automate region-of-interest annotation.
This example uses ECG signals from the publicly available QT Database [3] [4]. The data consists of roughly 15 minutes of ECG recordings, with a sample rate of 250 Hz, measured from a total of 105 patients. To obtain each recording, the examiners placed two electrodes on different locations on a patient's chest, resulting in a two-channel signal. The database provides signal region labels generated by an automated expert system [2]. This example aims to use a deep learning solution to provide a label for every ECG signal sample according to the region where the sample is located. This process of labeling regions of interest across a signal is often referred to as waveform segmentation.
To train a deep neural network to classify signal regions, you can use a Long Short-Term Memory (LSTM) network. This example shows how signal preprocessing techniques and time-frequency analysis can be used to improve LSTM segmentation performance. In particular, this example uses the Fourier synchrosqueezed transform to represent the nonstationary behavior of the ECG signal.
Download and Prepare the Data
Each channel of the 105 two-channel ECG signals was labeled independently by the automated expert system and is treated independently, for a total of 210 ECG signals that were stored together with the region labels in 210 MAT-files. The files are available at the following location: https://www.mathworks.com/supportfiles/SPT/data/QTDatabaseECGData.zip.
Download the data files into your temporary directory, whose location is specified by MATLAB®'s tempdir command. If you want to place the data files in a folder different from tempdir, change the directory name in the subsequent instructions.
% Download the data dataURL = 'https://www.mathworks.com/supportfiles/SPT/data/QTDatabaseECGData1.zip'; datasetFolder = fullfile(tempdir,'QTDataset'); zipFile = fullfile(tempdir,'QTDatabaseECGData.zip'); if ~exist(datasetFolder,'dir') websave(zipFile,dataURL); unzip(zipFile,tempdir); end
The unzip operation creates the QTDatabaseECGData folder in your temporary directory with 210 MAT-files in it. Each file contains an ECG signal in variable ecgSignal and a table of region labels in variable signalRegionLabels. Each file also contains the sample rate of the signal in variable Fs. In this example all signals have a sample rate of 250 Hz.
Create a signal datastore to access the data in the files. This example assumes the dataset has been stored in your temporary directory under the QTDatabaseECGData folder. If this is not the case, change the path to the data in the code below. Specify the signal variable names you want to read from each file using the SignalVariableNames parameter.
sds = signalDatastore(datasetFolder,'SignalVariableNames',["ecgSignal","signalRegionLabels"])
sds =
signalDatastore with properties:
Files:{
'/tmp/QTDataset/ecg1.mat';
'/tmp/QTDataset/ecg10.mat';
'/tmp/QTDataset/ecg100.mat'
... and 207 more
}
Folders: {'/tmp/QTDataset'}
AlternateFileSystemRoots: [0×0 string]
ReadSize: 1
SignalVariableNames: ["ecgSignal" "signalRegionLabels"]
ReadOutputOrientation: "column"
The datastore returns a two-element cell array with an ECG signal and a table of region labels each time you call the read function. Use the preview function of the datastore to see that the content of the first file is a 225,000 samples long ECG signal and a table containing 3385 region labels.
data = preview(sds)
data=2×1 cell array
{225000×1 double}
{ 3385×2 table }
Look at the first few rows of the region labels table and observe that each row contains the region limit indices and the region class value (P, T, or QRS).
head(data{2}) ROILimits Value
__________ _____
83 117 P
130 153 QRS
201 246 T
285 319 P
332 357 QRS
412 457 T
477 507 P
524 547 QRS
Visualize the labels for the first 1000 samples using a signalMask object.
M = signalMask(data{2});
plotsigroi(M,data{1}(1:1000))
The usual machine learning classification procedure is the following:
Divide the database into training and testing datasets.
Train the network using the training dataset.
Use the trained network to make predictions on the testing dataset.
The network is trained with 70% of the data and tested with the remaining 30%.
For reproducible results, reset the random number generator. Use the dividerand function to get random indices to shuffle the files, and the subset function of signalDatastore to divide the data into training and testing datastores.
rng default
[trainIdx,~,testIdx] = dividerand(numel(sds.Files),0.7,0,0.3);
trainDs = subset(sds,trainIdx);
testDs = subset(sds,testIdx);In this segmentation problem, the input to the LSTM network is an ECG signal and the output is a sequence or mask of labels with the same length as the input signal. The network task is to label each signal sample with the name of the region it belongs to. For this reason, it is necessary to transform the region labels on the dataset to sequences containing one label per signal sample. Use a transformed datastore and the getmask helper function to transform the region labels. The getmask function adds a label category, "n/a", to label samples that do not belong to any region of interest.
type getmask.mfunction outputCell = getmask(inputCell)
%GETMASK Convert region labels to a mask of labels of size equal to the
%size of the input ECG signal.
%
% inputCell is a two-element cell array containing an ECG signal vector
% and a table of region labels.
%
% outputCell is a two-element cell array containing the ECG signal vector
% and a categorical label vector mask of the same length as the signal.
% Copyright 2020 The MathWorks, Inc.
sig = inputCell{1};
roiTable = inputCell{2};
L = length(sig);
M = signalMask(roiTable);
% Get categorical mask and give priority to QRS regions when there is overlap
mask = catmask(M,L,'OverlapAction','prioritizeByList','PriorityList',[2 1 3]);
% Set missing values to "n/a"
mask(ismissing(mask)) = "n/a";
outputCell = {sig,mask};
end
Preview the transformed datastore to observe that it returns a signal vector and a label vector of equal lengths. Plot the first 1000 element of the categorical mask vector.
trainDs = transform(trainDs, @getmask); testDs = transform(testDs, @getmask); transformedData = preview(trainDs)
transformedData=1×2 cell array
{224993×1 double} {224993×1 categorical}
plot(transformedData{2}(1:1000))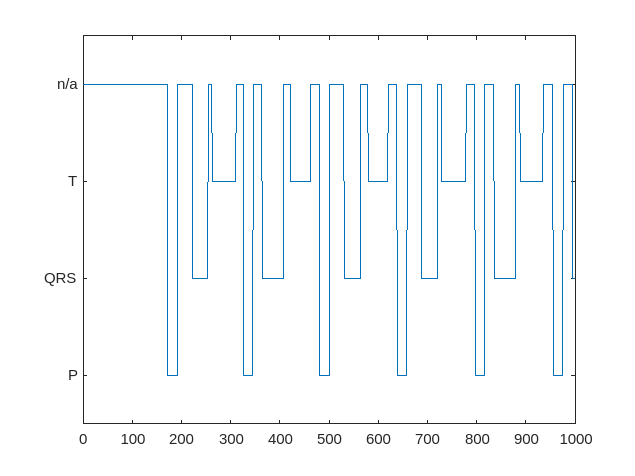
Passing very long input signals into the LSTM network can result in estimation performance degradation and excessive memory usage. To avoid these effects, break the ECG signals and their corresponding label masks using a transformed datastore and the resizeData helper function. The helper function creates as many 5000-sample segments as possible and discards the remaining samples. A preview of the output of the transformed datastore shows that the first ECG signal and its label mask are broken into 5000-sample segments. Note that preview of the transformed datastore only shows the first 8 elements of the otherwise floor(224993/5000) = 44 element cell array that would result if we called the datastore read function.
trainDs = transform(trainDs,@resizeData); testDs = transform(testDs,@resizeData); preview(trainDs)
ans=8×2 cell array
{[ 0 0 0 0 0 0 1 1 1 1 1 1 0 1 2 1 1 2 2 2 3 4 6 8 11 15 18 18 17 17 17 16 14 12 8 4 2 1 0 -1 -2 -1 0 0 0 1 2 2 2 2 1 0 -1 -1 -2 -3 -3 -2 -2 -2 -1 0 4 5 5 3 2 0 -1 -1 0 2 3 5 5 3 4 8 15 25 36 50 63 73 83 90 97 99 98 88 74 58 42 30 22 19 15 10 5 1 -1 -2 -2 -3 -4 -5 -6 -7 -9 -9 -10 -12 -13 -13 -12 -13 -14 -15 -15 -16 -18 -19 -20 -21 -22 -21 -22 -23 -24 -25 -25 -26 -27 -28 -29 -29 -28 -26 -25 -24 -23 -21 -19 -18 -16 -14 -12 -11 -9 -7 -6 -5 -5 -3 -3 -3 -3 -2 -2 -2 -2 -1 -1 -2 -2 -1 -1 -1 -1 0 0 0 -1 0 1 2 3 5 7 8 11 13 13 13 12 11 9 6 2 0 -2 -3 -5 -7 -8 -8 -7 -5 -4 -5 -4 -3 -4 -4 -5 -5 -6 -8 -9 -9 -8 -9 -9 -8 -6 -6 -4 -2 -3 -4 -5 -6 -7 -8 -8 -7 -6 -5 -6 -8 -7 -5 2 12 24 36 48 58 66 72 78 83 82 75 61 46 30 18 11 9 6 0 -4 -8 -9 -11 -12 -12 -13 -13 -14 -14 -15 -17 -17 -17 -17 -18 -18 -18 -19 -21 -22 -23 -23 -25 -25 -26 -26 -27 -28 -29 -30 -31 -32 -32 -33 -33 -34 -34 -34 -34 -32 -31 -30 -29 -27 -25 -23 -22 -19 -17 -15 -15 -14 -12 -11 -11 -9 -8 -8 -8 -8 -9 -9 -8 -8 -8 -8 -9 -8 -7 -7 -8 -8 -7 -7 -7 -6 -5 -3 -3 -1 2 4 5 6 7 6 5 4 2 -2 -5 -7 -7 -8 -10 -10 -10 -10 -9 -9 -7 -7 -6 -5 -5 -6 -8 -10 -11 -12 -12 -11 -11 -11 -10 -9 -7 -6 -5 -6 -7 -9 -11 -13 -14 -14 -14 -12 -11 -10 -11 -10 -6 0 10 22 35 47 58 68 76 80 83 78 67 51 36 22 12 6 3 -1 -6 -10 -12 -13 -14 -16 -17 -17 -17 -18 -18 -18 -19 -20 -20 -20 -20 -20 -19 -19 -20 -21 -22 -23 -25 -26 -26 -26 -26 -27 -27 -28 -28 -29 -28 -29 -28 -28 -29 -28 -27 -25 -25 -23 -22 -21 -19 -17 -15 -14 -12 -10 -9 -8 -7 -6 -5 -5 -5 -5 -5 -5 -5 -4 -4 -4 -3 -3 -3 -4 -3 -3 -3 -3 -4 -3 -4 -4 -2 -1 0 2 4 8 10 10 10 10 9 8 6 4 0 -3 -5 -5 -7 -9 -9 -8 -7 -8 -8 -7 -7 -7 -6 -6 -6 -7 -9 -9 -10 -11 -11 -11 -10 -10 -9 -7 -5 -3 -4 -5 -7 -9 -10 -11 -9 -8 -6 -4 -3 -4 -6 -5 0 6 16 27 40 51 60 68 75 82 81 77 66 52 39 27 17 10 6 2 -2 -6 -10 -12 -13 -14 -15 -16 -15 -16 -16 -17 -17 -17 -18 -18 -18 -17 -17 -16 -17 -17 -18 -19 -19 -20 -20 -21 -22 -23 -24 -25 -26 -26 -26 -26 -27 -26 -26 -26 -25 -24 -23 -22 -21 -19 -18 -16 -14 -11 -9 -8 -7 -5 -4 -4 -3 -2 -1 -1 -1 -1 -1 -2 -1 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 4 5 7 10 14 16 17 15 14 13 12 11 8 5 1 0 0 -2 -4 -4 -3 -3 -2 -1 0 0 0 -1 -2 -3 -5 -5 -5 -6 -6 -5 -5 -5 -4 -2 0 1 2 1 0 -3 -5 -5 -5 -4 -2 0 0 -1 -1 1 7 14 26 39 53 63 73 81 87 90 87 80 65 51 38 26 18 12 8 3 -2 -6 -8 -9 -10 -11 -12 -12 -12 -14 -13 -12 -12 -13 -13 -14 -15 -16 -17 -16 -17 -18 -18 -17 -18 -20 -21 -22 -22 -24 -24 -24 -24 -24 -24 -23 -24 -24 -24 -23 -22 -21 -19 -16 -14 -13 -11 -9 -7 -5 -3 0 0 1 2 3 4 4 4 6 6 6 6 7 8 7 7 7 7 6 6 8 8 8 8 9 9 9 10 11 12 12 14 15 17 19 22 25 27 27 27 27 25 22 19 15 13 11 11 10 9 8 7 8 8 8 9 9 10 10 9 9 7 5 5 6 6 5 5 5 6 6 9 12 13 11 9 6 4 1 1 4 6 7 9 9 8 9 14 23 34 48 62 77 86 96 103 109 110 103 92 76 61 45 34 29 25 19 11 6 2 0 0 -1 -3 -5 -6 -6 -6 -7 -7 -7 -7 -8 -8 -8 -9 -10 -11 -11 -11 -12 -14 -15 -15 -16 -17 -17 -18 -19 -20 -21 -21 -22 -22 -21 -21 -20 -19 -18 -16 -15 -13 -11 -9 -7 -4 -1 1 2 4 5 6 7 8 9 9 9 9 9 9 9 8 9 10 10 11 12 12 11 11 11 11 10 11 11 12 13 14 15 15 15 17 20 24 28 29 30 29 28 28 27 24 20 16 14 13 12 11 10 9 8 9 9 9 9 10 11 11 10 9 8 7 7 6 6 6 6 7 7 8 10 12 13 11 8 5 3 1 0 2 5 6 6 5 4 6 12 22 35 50 62 77 88 97 103 108 110 104 94 78 62 45 34 29 26 21 14 9 5 3 1 0 -1 -2 -3 -4 -4 -5 -6 -6 -5 -6 -8 -8 -8 -8 -9 -10 -10 -12 -13 -14 -15 -15 -16 -17 -17 -19 -21 -22 -22 -23 -24 -24 -23 -24 -24 -22 -20 -19 -17 -14 -12 -10 -9 -7 -5 -4 -3 -1 1 3 4 5 7 7 7 8 8 8 7 7 8 7 7 7 7 5 5 5 5 5 5 6 7 7 7 7 8 9 10 11 13 16 18 20 21 20 20 19 18 15 12 9 7 6 4 3 2 2 2 2 3 2 1 2 3 4 3 3 2 1 0 0 -1 -1 -2 -2 -1 0 1 2 2 0 -3 -5 -8 -9 -9 -8 -6 -5 -6 -6 -5 -1 7 20 35 49 62 74 84 92 99 105 103 94 77 58 39 25 19 16 12 6 0 -3 -6 -9 -11 -12 -12 -14 -14 -14 -14 -15 -15 -16 -17 -17 -18 -17 -17 -18 -18 -19 -20 -22 -23 -23 -24 -26 -27 -28 -29 -30 -31 -30 -31 -31 -33 -33 -33 -32 -30 -30 -28 -27 -25 -22 -20 -18 -16 -13 -10 -8 -6 -4 -2 -2 -2 -1 0 -1 0 0 0 0 0 1 0 0 0 1 1 1 0 1 2 2 2 3 3 3 4 5 6 7 9 13 16 19 19 19 18 18 17 16 13 9 6 4 3 1 0 -2 -2 -2 -1 0 0 1 1 1 1 0 0 0 -2 -3 -3 -2 -3 -3 -4 -2 -1 0 1 1 0 -2 -5 -6 -9 -9 -7 -5 -3 -1 -1 0 2 8 18 32 46 59 71 83 94 101 107 106 98 83 65 49 35 27 23 21 15 7 2 0 0 -2 -4 -4 -6 -7 -8 -8 -9 -9 -9 -8 -9 -9 -10 -9 -10 -11 -11 -11 -12 -13 -14 -15 -16 -18 -18 -19 -20 -21 -22 -23 -24 -24 -24 -24 -24 -24 -23 -21 -19 -17 -16 -14 -11 -9 -7 -5 -2 -1 1 2 2 2 3 4 4 4 4 4 4 4 5 5 4 3 4 5 5 4 4 4 4 5 5 7 6 6 6 7 8 9 12 15 19 20 21 19 18 18 18 16 12 8 5 4 4 2 1 0 0 0 1 3 3 3 4 4 4 3 2 1 1 0 0 1 1 0 1 1 2 3 3 3 1 0 -1 -3 -5 -5 -3 -1 0 0 0 1 4 10 21 34 47 60 71 82 89 97 100 100 93 80 66 47 34 26 23 19 13 7 3 1 -1 -2 -3 -4 -6 -7 -6 -6 -6 -6 -6 -6 -7 -8 -9 -9 -9 -10 -10 -11 -12 -14 -15 -16 -17 -18 -19 -19 -21 -21 -22 -23 -24 -25 -25 -24 -23 -23 -21 -20 -19 -18 -16 -12 -10 -7 -5 -4 -3 -2 -1 0 1 1 2 2 2 1 1 1 0 0 1 1 0 0 1 1 1 1 2 3 4 3 3 3 3 4 5 7 7 8 11 13 15 16 16 16 15 14 12 10 7 4 3 2 0 0 0 1 0 0 0 1 1 2 3 3 1 0 0 -1 -2 -3 -2 -2 -1 -1 0 0 1 2 2 1 -1 -4 -6 -7 -7 -6 -5 -4 -4 -5 -3 0 5 14 27 42 56 67 79 87 96 101 105 101 87 71 53 39 29 24 22 16 10 5 2 1 0 -1 -2 -3 … ]} {[n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a … ]}
{[ -34 -34 -33 -32 -31 -30 -28 -26 -24 -22 -20 -17 -15 -12 -10 -8 -6 -6 -5 -3 -3 -2 0 1 1 0 1 2 2 2 2 2 2 2 2 3 4 4 5 6 6 7 7 8 10 12 15 18 20 21 21 20 20 18 17 13 8 4 2 2 0 -2 -2 -1 0 -1 -1 0 0 1 1 1 0 -2 -3 -3 -3 -3 -3 -2 -2 -1 -1 1 3 5 6 4 2 -1 -3 -5 -6 -6 -4 -1 0 -1 -2 0 5 13 26 41 56 69 80 92 99 107 109 107 96 79 62 43 28 20 17 13 6 0 -3 -5 -6 -7 -8 -9 -11 -13 -13 -12 -11 -11 -12 -12 -14 -15 -16 -17 -17 -18 -19 -19 -19 -21 -23 -24 -26 -27 -28 -28 -28 -29 -30 -31 -31 -32 -33 -33 -32 -32 -31 -29 -27 -25 -23 -20 -18 -16 -14 -11 -8 -6 -5 -3 -1 0 1 2 2 1 2 2 2 2 3 3 4 4 3 3 3 3 4 4 5 5 6 8 8 8 11 14 17 19 20 21 20 19 18 17 13 8 6 5 4 2 0 0 0 0 1 1 1 0 0 1 1 0 -2 -3 -4 -4 -4 -3 -4 -4 -4 -3 -2 0 1 1 0 -3 -7 -9 -11 -11 -9 -5 -3 -4 -6 -5 -2 5 17 31 44 58 69 79 87 91 97 94 86 71 55 39 22 12 8 5 0 -6 -9 -12 -13 -14 -15 -15 -17 -19 -19 -19 -20 -20 -19 -19 -20 -21 -21 -22 -23 -24 -25 -25 -26 -28 -30 -31 -33 -35 -35 -35 -36 -37 -38 -39 -40 -40 -39 -39 -40 -39 -38 -37 -36 -35 -33 -30 -27 -26 -23 -21 -20 -19 -16 -15 -13 -12 -12 -12 -13 -13 -13 -13 -12 -12 -12 -11 -11 -12 -11 -11 -11 -12 -12 -12 -13 -13 -13 -12 -12 -12 -11 -10 -8 -5 -2 0 0 0 0 -1 -3 -6 -9 -11 -12 -14 -16 -18 -19 -20 -19 -18 -17 -17 -17 -16 -16 -17 -18 -18 -19 -20 -21 -22 -22 -22 -22 -21 -20 -20 -19 -17 -15 -17 -19 -21 -24 -26 -27 -27 -25 -24 -23 -24 -26 -28 -24 -16 -6 5 19 31 43 51 57 63 66 65 57 46 30 13 0 -8 -12 -14 -18 -22 -26 -28 -29 -30 -30 -31 -31 -32 -31 -33 -34 -34 -34 -34 -35 -35 -36 -37 -38 -39 -39 -41 -41 -43 -43 -45 -46 -46 -47 -48 -50 -50 -50 -51 -52 -51 -51 -52 -51 -49 -47 -47 -45 -43 -41 -39 -38 -35 -34 -32 -30 -28 -27 -26 -24 -23 -21 -21 -21 -21 -21 -23 -23 -22 -22 -22 -22 -21 -21 -22 -23 -24 -24 -24 -23 -22 -21 -20 -20 -19 -17 -15 -13 -11 -11 -11 -10 -11 -13 -17 -20 -22 -23 -24 -25 -26 -28 -28 -27 -26 -25 -26 -25 -23 -23 -24 -25 -26 -27 -28 -29 -29 -29 -30 -31 -30 -31 -30 -28 -26 -25 -26 -28 -31 -33 -36 -37 -37 -36 -34 -35 -35 -37 -36 -32 -24 -14 -2 10 22 32 40 47 54 58 57 51 38 23 6 -7 -14 -17 -20 -24 -29 -32 -34 -35 -36 -38 -40 -41 -41 -42 -41 -42 -43 -44 -45 -44 -45 -46 -47 -47 -47 -48 -48 -49 -50 -52 -52 -53 -53 -54 -55 -55 -57 -56 -58 -57 -58 -57 -58 -58 -57 -57 -54 -54 -51 -50 -47 -44 -41 -38 -38 -36 -35 -32 -32 -31 -29 -30 -30 -30 -30 -31 -31 -31 -30 -31 -31 -30 -30 -30 -31 -30 -29 -30 -29 -28 -26 -26 -25 -25 -23 -21 -18 -16 -15 -15 -15 -15 -15 -17 -19 -22 -25 -27 -27 -28 -29 -31 -31 -30 -30 -30 -31 -30 -30 -30 -31 -31 -31 -33 -33 -34 -34 -35 -35 -35 -34 -33 -32 -29 -27 -27 -29 -31 -33 -36 -37 -38 -36 -37 -36 -35 -36 -36 -33 -25 -17 -5 8 22 34 44 54 64 71 72 65 51 35 18 4 -4 -9 -12 -18 -24 -28 -31 -32 -34 -35 -36 -36 -37 -37 -37 -37 -37 -38 -39 -39 -39 -38 -39 -38 -40 -40 -43 -44 -44 -44 -45 -46 -46 -47 -47 -48 -48 -50 -52 -52 -52 -51 -52 -50 -50 -49 -47 -45 -42 -41 -39 -38 -35 -34 -33 -32 -30 -29 -28 -26 -25 -24 -24 -23 -22 -22 -22 -22 -21 -21 -21 -20 -19 -19 -19 -19 -18 -17 -16 -15 -13 -11 -11 -9 -5 -3 -2 0 3 3 2 2 2 2 0 -4 -7 -9 -11 -12 -14 -16 -17 -16 -14 -14 -14 -13 -12 -12 -13 -13 -15 -16 -17 -17 -16 -16 -16 -17 -16 -16 -15 -13 -10 -7 -8 -9 -11 -13 -16 -17 -15 -13 -10 -9 -9 -10 -10 -7 0 10 21 34 48 59 69 77 84 89 87 81 68 53 38 24 16 11 6 1 -4 -8 -11 -11 -12 -13 -14 -14 -14 -15 -16 -17 -16 -16 -17 -18 -18 -18 -19 -20 -21 -22 -23 -23 -23 -24 -25 -26 -27 -28 -30 -30 -30 -30 -32 -33 -34 -35 -35 -35 -33 -32 -30 -28 -26 -25 -23 -20 -17 -14 -12 -10 -9 -8 -6 -4 -4 -3 -3 -1 -1 -2 -2 -2 -1 -1 0 1 1 0 1 3 3 3 3 5 6 8 11 14 16 17 18 18 18 18 15 13 9 6 5 5 3 1 0 0 1 1 1 2 2 2 2 2 1 0 0 -1 -1 -2 -2 0 0 0 0 2 5 7 8 8 7 4 2 0 0 0 2 4 4 2 1 1 5 12 23 37 51 64 74 85 92 99 102 98 89 75 60 44 31 23 22 19 14 8 3 1 0 0 0 0 -1 -3 -4 -4 -4 -5 -6 -6 -8 -8 -9 -10 -11 -13 -14 -15 -16 -18 -19 -20 -22 -24 -26 -27 -29 -30 -30 -30 -29 -30 -30 -29 -28 -27 -25 -23 -22 -20 -17 -15 -13 -10 -7 -5 -4 -2 -1 -1 0 0 1 2 3 2 3 2 2 3 4 5 5 5 6 5 5 5 5 5 6 6 9 12 15 16 18 18 17 17 16 14 10 8 7 6 4 2 0 0 1 2 2 2 1 1 1 1 1 1 0 0 -2 -1 -1 0 -1 -1 -1 0 1 3 5 5 3 0 -1 -2 -4 -4 -2 0 0 -1 -3 -3 -1 3 12 25 35 46 56 66 74 81 88 90 88 78 67 52 37 27 23 21 16 10 6 3 2 2 2 1 0 -1 -2 -2 -2 -2 -2 -2 -3 -5 -6 -7 -8 -9 -9 -10 -11 -12 -13 -14 -15 -16 -17 -17 -18 -18 -19 -20 -21 -21 -20 -19 -19 -18 -17 -14 -13 -13 -11 -10 -10 -9 -7 -4 -2 -1 0 0 0 2 4 4 4 4 5 5 5 5 5 6 6 6 6 5 5 6 8 9 10 12 14 16 19 20 21 21 19 19 19 18 16 13 11 9 7 6 6 7 8 8 8 8 8 10 10 10 9 9 9 9 9 9 9 9 8 8 9 10 11 13 14 14 12 10 8 7 6 6 9 11 13 13 12 13 17 27 39 53 65 78 89 102 112 119 124 119 109 91 75 59 48 43 39 34 27 22 20 19 17 16 15 13 11 10 10 10 9 7 6 4 2 1 0 0 -1 -2 -2 -2 -4 -6 -7 -9 -9 -9 -8 -8 -9 -11 -12 -13 -13 -12 -10 -9 -7 -6 -5 -4 -4 0 2 5 6 9 11 13 14 15 17 19 20 20 21 21 21 22 22 22 21 22 22 24 24 25 26 25 25 26 28 29 32 35 39 42 44 45 45 45 44 44 42 41 38 34 32 29 28 28 28 28 28 28 29 29 29 28 27 25 24 23 24 24 24 24 24 23 23 25 27 30 31 32 31 29 27 25 26 27 29 32 35 34 33 33 36 43 53 66 79 93 102 113 122 129 134 133 129 115 102 87 73 63 58 56 50 45 38 34 32 30 28 27 26 25 24 23 23 23 … ]} {[T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T … ]}
{[12 11 10 9 7 7 6 4 4 4 4 3 2 2 2 1 0 0 -1 -2 -4 -5 -7 -9 -10 -11 -11 -12 -12 -13 -14 -15 -16 -16 -17 -17 -17 -17 -17 -17 -16 -14 -12 -10 -7 -4 -1 1 3 6 9 11 13 14 15 16 16 17 18 19 19 20 20 20 21 21 22 22 22 23 23 23 24 25 27 28 30 32 35 38 40 40 41 40 40 40 39 37 33 30 26 23 21 22 22 23 23 22 22 21 22 21 22 22 20 19 18 18 17 17 17 17 17 18 21 24 25 25 24 21 18 15 15 15 16 18 21 22 20 19 22 30 40 53 69 83 96 107 117 126 131 132 124 110 90 69 51 39 35 34 31 26 20 17 16 15 13 11 10 10 8 6 6 5 5 4 4 4 2 0 -3 -5 -6 -5 -4 -4 -6 -9 -11 -13 -15 -17 -18 -19 -21 -21 -21 -20 -21 -25 -27 -25 -21 -20 -18 -15 -14 -13 -12 -8 -7 -5 -2 0 3 3 3 4 4 6 7 6 5 5 7 7 7 8 10 11 10 9 8 9 10 11 14 15 17 18 22 26 28 30 31 32 31 30 29 28 25 22 19 15 14 14 15 15 14 12 13 13 14 13 13 12 10 9 9 9 9 8 7 6 7 8 10 14 15 14 14 13 11 8 6 6 8 10 14 15 14 11 12 18 27 39 54 69 82 92 98 105 109 109 102 86 68 48 32 21 17 16 13 9 5 2 1 0 0 -1 -2 -3 -4 -5 -7 -7 -8 -9 -10 -9 -11 -12 -12 -14 -14 -15 -15 -17 -18 -20 -21 -22 -24 -25 -26 -26 -26 -27 -27 -27 -27 -27 -26 -25 -23 -21 -19 -16 -14 -11 -10 -7 -5 -3 0 3 5 7 8 8 8 8 9 10 11 11 12 13 13 13 14 15 15 16 17 18 19 19 22 24 27 29 33 34 35 35 36 36 34 32 30 27 24 21 20 19 19 19 20 19 18 18 18 19 19 19 18 17 15 14 14 15 15 15 16 17 18 20 23 24 23 21 20 19 17 17 18 20 21 21 20 18 19 23 32 45 57 69 80 91 97 104 110 116 117 111 102 85 68 53 44 41 40 36 30 25 21 19 18 17 16 16 16 15 14 11 11 11 11 11 10 9 7 6 5 5 4 3 2 1 0 -2 -3 -3 -4 -5 -6 -6 -7 -8 -7 -7 -7 -6 -5 -2 -1 0 2 4 6 8 10 13 16 18 21 23 24 25 26 27 28 28 30 30 31 31 32 33 34 34 34 34 34 35 36 39 40 40 42 45 48 50 53 52 51 50 50 51 49 48 44 42 39 36 36 36 37 36 37 37 37 36 36 36 34 34 34 35 35 34 34 34 33 33 35 36 38 39 39 39 39 38 35 33 31 31 32 34 36 35 34 34 37 43 53 67 79 92 103 115 123 132 138 139 134 118 103 86 73 65 61 58 50 44 39 38 35 34 34 32 30 28 28 27 27 26 25 25 24 22 21 20 19 18 17 16 14 13 12 11 11 9 8 8 6 4 3 3 3 4 4 5 5 6 7 8 10 11 13 15 18 19 21 24 25 26 27 29 30 31 32 32 33 32 33 34 35 35 36 37 36 36 35 36 36 36 39 40 42 44 47 49 52 52 52 51 50 49 46 46 43 40 36 34 32 31 32 32 32 31 31 31 31 30 29 28 26 25 25 25 24 24 25 26 27 28 30 32 31 29 28 26 24 22 22 23 24 25 25 24 22 24 31 41 52 66 78 92 100 109 115 122 123 116 105 87 71 57 50 46 42 36 29 25 21 20 18 17 16 15 14 13 11 10 11 10 8 7 7 5 4 3 2 1 0 -1 -2 -3 -4 -6 -8 -9 -10 -11 -11 -12 -13 -13 -12 -13 -13 -13 -12 -10 -9 -7 -5 -4 -3 -1 0 1 3 5 7 8 9 9 10 10 10 10 10 10 10 11 11 12 11 12 12 12 11 13 14 15 17 20 23 25 27 28 28 27 26 26 25 23 19 17 13 10 9 9 9 9 8 8 8 7 7 7 6 4 3 3 2 1 0 0 0 1 2 3 5 7 7 7 4 2 -1 -2 -2 -1 0 2 3 1 1 3 8 16 27 41 54 66 75 85 91 97 97 92 81 64 49 34 23 18 16 13 7 2 -1 -2 -3 -5 -7 -8 -9 -10 -11 -12 -13 -14 -15 -15 -17 -18 -18 -18 -18 -20 -21 -22 -23 -25 -26 -28 -29 -30 -31 -31 -32 -33 -34 -34 -35 -35 -34 -33 -32 -32 -30 -28 -26 -24 -21 -18 -15 -14 -12 -9 -7 -6 -5 -3 -2 -2 -2 -1 -1 -1 0 0 0 0 0 2 2 2 2 3 3 5 7 9 11 14 16 16 17 16 16 16 15 13 10 7 3 0 -1 -1 -2 -2 -1 -1 -1 -2 -2 -1 -2 -4 -5 -5 -6 -6 -5 -5 -5 -5 -5 -3 -1 0 2 2 0 -2 -4 -6 -7 -6 -5 -3 -3 -5 -6 -6 -2 6 19 33 47 58 68 79 85 92 94 95 85 71 54 35 21 14 13 10 4 0 -3 -5 -6 -8 -10 -12 -12 -12 -14 -15 -15 -15 -15 -16 -18 -19 -19 -18 -19 -21 -22 -23 -23 -24 -25 -27 -29 -29 -30 -31 -34 -35 -35 -35 -34 -34 -34 -33 -33 -33 -31 -29 -27 -25 -22 -19 -17 -15 -14 -12 -11 -8 -6 -5 -4 -3 -2 -2 -2 -1 -1 -1 -2 -1 -1 0 0 0 0 1 1 1 2 3 5 6 10 13 15 16 16 16 15 15 13 10 7 4 2 0 -1 -2 -1 -1 -2 -2 -1 -1 -1 -1 -1 -2 -4 -4 -4 -5 -4 -4 -4 -3 -3 -2 0 2 3 3 2 0 -2 -5 -6 -5 -4 -1 1 0 0 0 6 14 26 41 57 71 82 94 100 107 107 104 90 74 57 40 28 22 20 15 7 1 0 0 0 -1 -2 -3 -6 -8 -9 -8 -8 -10 -13 -15 -15 -14 -15 -16 -18 -20 -21 -22 -22 -24 -25 -27 -30 -31 -29 -29 -32 -36 -37 -36 -35 -34 -33 -34 -33 -31 -28 -27 -27 -25 -22 -18 -16 -15 -17 -18 -18 -15 -11 -7 -7 -9 -9 -8 -8 -9 -9 -8 -7 -7 -6 -5 -6 -7 -6 -5 -5 -4 -1 1 4 6 8 9 7 7 7 5 1 -3 -5 -7 -9 -12 -12 -12 -12 -12 -12 -11 -11 -11 -10 -8 -8 -9 -11 -13 -16 -17 -16 -18 -18 -17 -16 -16 -17 -16 -13 -11 -11 -12 -13 -15 -17 -17 -16 -14 -13 -14 -16 -16 -13 -7 1 14 29 43 57 67 75 81 84 85 76 65 50 35 20 8 3 1 -3 -10 -15 -16 -16 -17 -20 -23 -24 -25 -26 -30 -32 -32 -31 -31 -32 -33 -34 -33 -34 -36 -38 -39 -40 -41 -42 -43 -45 -45 -45 -46 -49 -52 -54 -53 -53 -53 -52 -51 -51 -50 -47 -46 -44 -43 -40 -38 -37 -34 -32 -29 -28 -27 -26 -24 -23 -23 -22 -21 -20 -20 -20 -21 -21 -20 -19 -18 -18 -17 -17 -16 -16 -16 -14 -12 -9 -6 -2 0 0 0 0 0 0 -1 -3 -5 -8 -10 -12 -13 -14 -14 -12 -12 -12 -13 -12 -11 -12 -13 -13 -14 -15 -15 -15 -15 -15 -16 -15 -15 -15 -12 -9 -7 -8 -9 -11 -12 -14 -14 -13 -11 -10 -9 -8 -10 -8 -3 6 18 31 44 58 67 76 84 91 94 88 78 60 44 27 15 9 8 4 0 -6 -9 -12 -13 -13 -14 -15 -15 -15 -16 -18 -19 -20 -20 -21 -21 -21 -22 -24 -24 -25 -26 -27 -27 -29 -31 -32 -33 -34 -35 -36 -36 -37 -37 -38 -38 -38 -38 -37 -36 -34 -33 -30 -28 -25 -24 -22 -20 -18 -15 -14 -12 -10 -8 -8 -7 -6 -5 -5 -3 -2 -2 -2 -1 -1 -1 0 0 0 0 1 2 3 4 6 9 11 13 14 15 15 15 14 11 7 3 2 1 0 -2 -2 -1 -2 -2 -2 -2 -2 -2 -1 -1 … ]} {[n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a P P P P P P P P P P P P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a P P P P P P P P P P P P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a … ]}
{[ -2 -1 -1 0 0 -1 -1 -1 -2 -3 -3 -4 -4 -4 -3 -2 -2 -2 -1 1 3 2 1 0 -3 -6 -8 -9 -8 -8 -7 -4 -4 -5 -3 4 14 27 42 60 74 86 96 106 115 116 110 92 73 52 37 27 22 17 10 4 0 -2 -3 -3 -5 -7 -7 -7 -7 -8 -9 -10 -10 -11 -12 -12 -13 -14 -15 -14 -14 -15 -17 -17 -19 -20 -22 -22 -24 -25 -26 -27 -27 -29 -30 -30 -30 -30 -30 -28 -27 -25 -24 -22 -21 -21 -20 -18 -16 -14 -11 -9 -8 -8 -7 -5 -4 -5 -6 -6 -7 -6 -5 -5 -5 -6 -6 -6 -6 -6 -6 -5 -4 -5 -5 -4 -4 -3 -2 0 2 5 7 9 10 9 8 7 6 3 0 -2 -4 -7 -9 -9 -10 -10 -9 -8 -8 -8 -8 -9 -9 -11 -13 -13 -14 -15 -16 -15 -14 -15 -14 -14 -12 -12 -10 -7 -5 -6 -8 -10 -13 -16 -17 -17 -15 -15 -14 -15 -16 -16 -12 -5 7 22 37 51 64 75 85 92 99 98 88 73 56 40 24 16 12 7 0 -6 -10 -13 -15 -16 -15 -15 -16 -18 -18 -20 -22 -23 -22 -21 -21 -23 -23 -24 -26 -26 -27 -27 -29 -30 -31 -34 -35 -37 -36 -38 -39 -40 -41 -40 -42 -41 -42 -41 -42 -42 -40 -38 -35 -34 -31 -30 -28 -26 -23 -19 -18 -15 -13 -11 -12 -13 -12 -11 -10 -10 -10 -9 -9 -9 -9 -9 -9 -9 -7 -6 -6 -6 -5 -5 -5 -4 -2 0 1 3 7 10 11 11 10 9 9 10 8 6 2 0 -2 -4 -6 -6 -4 -5 -5 -5 -4 -3 -4 -4 -5 -6 -7 -8 -8 -9 -9 -10 -8 -8 -8 -7 -5 -3 -2 -2 -3 -5 -7 -9 -10 -12 -13 -12 -9 -8 -9 -10 -8 -3 5 17 32 46 56 65 73 81 87 90 86 74 58 42 27 15 9 7 3 -2 -7 -10 -10 -11 -13 -14 -13 -14 -15 -15 -16 -16 -17 -18 -18 -19 -20 -21 -22 -22 -23 -24 -23 -25 -27 -29 -29 -29 -30 -30 -31 -31 -32 -33 -33 -33 -33 -34 -32 -31 -31 -31 -30 -28 -26 -24 -22 -18 -16 -15 -14 -13 -12 -10 -8 -7 -6 -6 -4 -4 -4 -4 -4 -3 -3 -3 -2 -2 -2 -1 -1 -1 -1 -1 0 1 2 3 6 9 12 14 15 15 14 14 13 12 9 6 3 1 0 -2 -2 -1 0 0 1 2 1 1 1 1 0 0 0 0 -1 -2 -2 -2 -2 -2 0 1 3 4 6 5 4 2 0 0 -1 -1 0 0 0 -1 -2 -2 0 8 18 30 42 54 64 74 81 88 93 94 88 75 59 42 28 22 20 19 12 8 5 3 1 0 0 -1 -2 -2 -2 -2 -4 -5 -5 -6 -8 -8 -7 -8 -8 -10 -11 -12 -13 -14 -15 -16 -17 -17 -18 -18 -19 -20 -21 -22 -24 -24 -23 -23 -23 -22 -21 -19 -19 -16 -14 -11 -9 -6 -4 -2 -1 0 1 2 3 3 5 4 4 4 4 4 4 4 4 5 4 5 5 5 4 5 7 8 9 10 12 15 18 21 22 22 20 21 20 19 16 13 10 8 5 4 4 4 5 6 6 5 4 6 7 7 6 6 5 3 3 3 3 2 2 3 3 4 7 10 10 8 7 5 2 1 1 3 3 3 3 3 2 4 11 23 35 51 65 81 92 101 110 118 120 110 95 75 55 40 32 28 22 15 8 5 4 2 2 1 0 -2 -3 -4 -5 -5 -6 -5 -6 -7 -8 -9 -10 -10 -11 -12 -14 -16 -17 -17 -19 -20 -21 -22 -24 -25 -25 -25 -25 -27 -26 -26 -26 -25 -23 -21 -20 -19 -18 -16 -14 -12 -9 -4 -2 -1 0 2 4 4 5 5 4 3 4 5 5 5 6 7 7 7 7 7 7 7 8 9 10 11 12 13 14 16 20 24 27 28 26 25 24 22 20 17 15 12 10 7 5 4 5 6 5 4 5 6 7 8 7 6 4 1 1 1 1 1 2 2 3 4 6 9 10 10 9 7 3 0 0 1 3 5 7 7 4 3 5 13 25 40 55 72 86 97 107 114 121 119 113 97 79 62 46 36 30 27 20 14 9 7 5 4 4 2 2 2 1 0 -1 -2 -4 -5 -5 -6 -7 -8 -9 -9 -10 -11 -11 -12 -13 -15 -17 -18 -18 -20 -21 -21 -21 -22 -23 -22 -22 -22 -22 -21 -20 -20 -18 -16 -14 -12 -9 -5 -1 0 1 3 4 5 6 8 9 9 10 11 11 11 11 12 12 12 12 13 14 13 13 14 15 15 16 18 19 20 22 26 29 31 32 33 33 32 31 29 25 20 17 17 17 16 14 14 15 15 14 15 15 15 15 15 15 14 13 13 12 11 10 12 13 14 14 15 17 18 21 21 21 19 17 15 14 12 13 15 15 15 13 12 14 21 31 45 60 73 87 98 110 117 125 127 121 108 89 72 54 44 40 38 32 25 20 18 16 15 13 13 12 11 10 10 9 7 6 5 5 5 5 5 3 1 0 0 -1 -2 -3 -4 -5 -6 -7 -8 -10 -11 -11 -12 -12 -12 -12 -12 -11 -10 -9 -7 -6 -4 -2 0 1 3 5 8 10 11 14 15 16 16 17 18 18 19 19 20 20 20 20 21 21 21 21 22 23 22 23 24 26 28 31 36 38 39 39 39 38 36 35 32 28 26 25 25 23 22 21 22 22 22 22 23 23 23 24 23 22 20 19 19 19 19 18 19 19 19 20 22 25 26 27 26 25 22 20 18 17 18 19 21 21 21 19 22 27 37 49 64 79 91 104 115 126 132 134 130 115 99 81 67 55 49 45 40 33 28 25 23 22 20 18 17 17 16 15 15 15 13 12 12 12 10 9 9 8 7 6 5 4 2 1 0 0 -1 -2 -2 -3 -4 -5 -6 -7 -8 -7 -6 -5 -5 -4 -2 0 0 2 4 6 8 10 12 14 15 17 18 19 20 20 21 21 21 20 20 20 20 21 22 22 22 22 23 24 24 24 26 29 31 34 38 39 38 37 37 36 33 30 27 25 23 22 21 19 17 17 19 20 19 19 19 19 17 16 15 14 13 11 12 12 12 12 12 13 13 15 17 20 20 19 17 14 12 9 10 11 12 13 15 14 13 14 21 32 44 58 71 85 95 106 114 120 122 115 102 83 66 51 42 37 34 28 21 17 14 12 11 10 8 7 6 4 3 2 1 0 0 0 -1 -2 -4 -5 -5 -6 -6 -8 -9 -10 -12 -14 -15 -15 -16 -18 -19 -20 -21 -21 -21 -22 -22 -21 -20 -18 -16 -14 -12 -10 -9 -7 -5 -2 0 1 3 3 3 4 5 6 7 6 6 7 7 7 7 8 9 9 8 8 8 8 10 11 12 12 15 17 20 21 22 23 22 22 20 19 15 11 9 7 6 4 3 3 3 3 3 4 3 2 3 3 3 2 1 0 -1 -1 0 0 -1 -2 -1 0 1 3 6 6 5 3 1 -1 -3 -4 -4 -2 -1 0 0 0 1 7 17 30 43 56 68 80 88 94 101 102 95 81 65 48 33 24 21 19 14 8 4 1 0 -2 -3 -5 -6 -7 -8 -8 -10 -11 -11 -12 -13 -14 -14 -15 -16 -17 -18 -19 -21 -22 -23 -24 -26 -26 -27 -29 -30 -31 -31 -32 -32 -33 -33 -33 -33 -32 -31 -29 -27 -24 -22 -20 -19 -16 -13 -11 -9 -7 -5 -5 -5 -4 -2 -2 -3 -2 -2 -3 -4 -3 -2 -2 -2 -1 0 0 0 0 1 1 2 5 9 12 13 13 13 12 10 9 6 3 0 -2 -2 -4 -5 -6 -7 -7 -7 -7 -6 -6 -6 -5 -4 -5 -6 -8 -8 -9 -9 -9 -8 -8 -9 -9 -9 -7 -5 -2 0 -1 -4 -7 -9 -11 -12 -11 -8 -6 -5 -5 -6 -4 -1 7 20 36 51 66 80 92 101 109 113 107 92 74 56 39 27 22 17 11 3 -1 -3 -4 -5 -7 -8 -9 -11 -11 -12 -12 -14 -14 -14 -15 -17 -18 -18 -19 -20 -21 -22 -22 -24 -25 -26 -27 -28 -30 -30 -31 -31 -32 -32 -32 -32 -33 -32 -31 -30 -29 -27 -25 -24 -21 -19 -16 -14 -12 -10 -8 -6 -5 -5 -4 … ]} {[n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS … ]}
{[52 62 69 78 84 87 86 77 65 49 34 22 15 14 12 8 2 -1 -3 -4 -4 -4 -4 -4 -5 -6 -5 -4 -5 -7 -8 -8 -8 -8 -8 -8 -9 -10 -10 -10 -11 -12 -12 -13 -15 -16 -18 -18 -19 -19 -20 -21 -22 -22 -20 -19 -18 -18 -16 -14 -14 -12 -9 -6 -6 -6 -5 -1 0 0 1 1 1 0 1 2 3 4 5 4 3 3 4 4 5 5 5 5 6 5 6 6 6 6 7 10 11 14 17 19 18 16 15 17 18 18 15 11 7 4 4 4 3 1 2 3 4 4 5 6 7 6 5 5 5 5 4 3 2 1 1 1 1 1 1 3 5 6 7 7 6 3 1 -1 -2 -3 -3 0 0 -1 -3 -2 0 6 15 28 40 51 62 71 81 87 94 95 87 75 58 43 29 21 17 13 8 3 0 -1 -2 -4 -4 -5 -6 -7 -6 -5 -4 -4 -6 -7 -8 -9 -10 -9 -9 -10 -11 -12 -12 -14 -16 -18 -19 -21 -22 -22 -22 -23 -25 -26 -28 -28 -28 -27 -27 -27 -26 -26 -25 -24 -22 -21 -20 -18 -14 -13 -12 -12 -11 -9 -7 -6 -5 -5 -6 -7 -6 -5 -5 -6 -6 -6 -6 -6 -7 -7 -8 -8 -7 -8 -8 -7 -5 -3 -3 -3 -1 1 3 3 4 4 3 1 0 -2 -6 -9 -10 -11 -12 -13 -14 -15 -16 -16 -16 -15 -16 -16 -16 -15 -17 -19 -19 -19 -19 -20 -18 -18 -18 -19 -19 -19 -19 -17 -16 -16 -17 -18 -20 -24 -27 -30 -29 -28 -27 -27 -27 -27 -27 -23 -16 -5 7 22 39 54 63 73 81 90 88 77 60 39 20 6 0 -1 -6 -12 -18 -22 -25 -26 -26 -28 -29 -30 -29 -29 -31 -33 -34 -34 -35 -34 -34 -35 -36 -38 -40 -43 -45 -45 -44 -44 -46 -48 -49 -49 -50 -51 -53 -55 -55 -56 -55 -55 -54 -53 -51 -50 -49 -48 -47 -44 -43 -40 -37 -34 -34 -33 -31 -31 -29 -29 -27 -28 -29 -29 -28 -27 -27 -26 -26 -25 -25 -25 -25 -26 -27 -27 -26 -26 -25 -23 -21 -21 -19 -17 -14 -13 -13 -12 -12 -12 -11 -11 -13 -17 -21 -23 -25 -26 -27 -29 -30 -30 -29 -28 -28 -27 -26 -25 -24 -26 -27 -27 -26 -27 -28 -28 -28 -28 -28 -27 -27 -26 -25 -23 -21 -22 -24 -26 -27 -30 -32 -32 -30 -28 -27 -27 -27 -26 -22 -13 -1 12 28 44 59 72 81 90 95 91 80 62 45 26 12 4 0 -3 -10 -16 -20 -23 -25 -25 -25 -25 -27 -27 -28 -28 -28 -28 -29 -30 -31 -32 -31 -32 -33 -34 -34 -36 -38 -38 -39 -39 -41 -42 -43 -43 -43 -45 -44 -46 -46 -46 -45 -45 -45 -43 -43 -40 -39 -36 -34 -32 -29 -27 -23 -21 -19 -19 -17 -15 -15 -14 -13 -12 -13 -13 -12 -11 -10 -9 -8 -7 -8 -9 -8 -7 -7 -8 -6 -5 -4 -3 -2 0 1 4 7 9 9 10 11 11 10 7 4 1 -1 -2 -3 -5 -5 -5 -5 -3 -3 -3 -3 -2 -1 0 0 -1 -3 -5 -6 -6 -6 -5 -4 -3 -3 -4 -3 0 3 4 2 0 -3 -4 -5 -4 -5 -4 -2 -1 -2 -2 0 6 15 28 43 58 71 82 94 103 110 111 106 93 76 60 44 32 26 23 18 12 8 7 7 5 4 4 5 4 3 2 2 2 1 0 0 -1 -1 -2 -2 -3 -4 -4 -4 -5 -7 -8 -8 -9 -10 -11 -11 -12 -13 -14 -14 -14 -15 -14 -13 -12 -12 -11 -8 -6 -4 -1 2 4 6 8 10 12 14 14 15 16 16 17 18 18 18 19 20 21 21 21 22 22 22 22 22 23 24 25 26 27 27 28 31 34 37 38 40 39 40 40 39 36 31 28 26 26 24 23 22 22 22 24 25 25 25 25 27 26 25 24 23 22 20 20 21 22 21 22 24 25 27 28 30 30 29 27 25 23 21 21 21 23 23 24 22 22 23 30 41 54 68 81 93 104 113 121 127 129 121 108 92 74 58 48 46 43 39 32 29 26 24 23 23 23 21 20 19 18 18 17 18 17 16 15 15 14 13 13 12 11 10 9 10 11 10 8 7 7 7 7 7 6 4 3 3 4 4 5 6 8 9 10 13 16 18 20 22 24 24 25 27 29 30 30 30 31 30 31 32 32 32 31 33 35 35 33 33 34 35 37 37 38 37 38 41 43 46 46 47 47 46 45 45 43 38 35 33 33 31 30 29 30 30 30 31 32 32 32 33 33 32 30 29 29 29 29 29 29 28 28 28 29 30 31 33 34 33 31 29 27 25 25 27 28 29 29 28 27 29 34 44 56 68 80 89 100 107 116 121 123 117 105 91 74 60 52 51 47 42 36 34 33 32 32 30 29 27 25 25 24 22 21 22 22 22 20 20 20 19 19 19 19 18 17 15 14 12 10 10 10 9 7 7 7 6 5 7 8 8 8 9 10 12 13 15 17 19 21 23 26 28 29 30 31 30 31 31 32 32 33 33 33 34 33 34 34 34 34 34 36 36 36 36 37 37 39 41 43 46 45 46 46 47 47 45 43 39 36 34 34 32 30 29 29 30 30 30 30 31 32 33 33 33 32 30 29 28 29 29 29 28 27 27 28 29 30 31 31 30 29 27 26 24 23 23 25 26 27 27 26 28 32 40 51 63 75 84 97 104 112 115 115 108 95 81 64 51 43 42 41 36 31 26 25 23 22 19 18 17 14 15 15 14 13 12 11 9 8 7 7 6 5 5 5 5 3 2 1 0 0 -1 -2 -3 -3 -3 -4 -4 -5 -6 -6 -6 -7 -5 -2 0 0 2 5 7 8 10 12 13 13 13 15 15 16 16 17 18 18 20 21 20 18 19 20 19 18 17 18 18 19 20 21 23 24 26 28 29 30 31 33 32 29 26 22 19 17 17 15 13 12 13 13 13 13 13 14 14 14 13 13 12 12 12 12 11 10 9 9 8 8 10 12 13 14 14 13 10 7 5 4 4 4 6 6 4 2 2 6 13 23 35 48 58 69 79 89 95 101 100 90 76 58 43 30 22 19 16 12 6 3 2 0 0 -1 -2 -4 -5 -6 -7 -8 -9 -10 -11 -11 -12 -14 -14 -15 -16 -18 -17 -17 -18 -20 -21 -22 -23 -24 -25 -25 -26 -27 -28 -28 -29 -29 -27 -26 -25 -24 -23 -21 -19 -18 -17 -15 -14 -12 -10 -8 -6 -5 -4 -3 -3 -2 -1 -1 -1 -1 0 1 1 1 0 0 0 -1 0 1 2 2 2 3 5 6 9 11 11 10 10 12 12 11 8 5 3 1 1 0 -1 -2 -1 0 -1 -2 -1 0 1 1 1 1 0 -1 -2 -2 -3 -3 -3 -3 -3 -3 -1 1 3 4 3 2 0 -3 -6 -7 -7 -7 -7 -6 -6 -6 -2 2 10 20 32 45 55 67 76 86 94 97 95 81 65 46 30 20 15 12 7 1 -2 -4 -5 -6 -8 -9 -8 -9 -10 -11 -11 -11 -13 -13 -14 -14 -15 -17 -17 -17 -18 -18 -19 -19 -20 -21 -22 -24 -25 -26 -26 -27 -29 -29 -29 -29 -28 -29 -28 -27 -27 -26 -24 -21 -20 -18 -16 -14 -13 -12 -10 -8 -7 -6 -4 -4 -4 -2 0 0 0 0 1 1 0 0 0 0 0 1 2 1 1 2 3 4 5 6 9 11 13 14 15 15 15 15 14 10 7 4 4 3 2 1 1 3 3 3 3 3 3 5 6 6 5 5 4 2 1 1 2 3 3 3 3 4 4 6 8 9 7 7 6 4 2 0 0 0 0 1 1 1 3 9 19 31 43 56 69 81 92 102 113 112 105 88 69 50 35 28 24 20 14 9 6 4 2 1 1 0 -1 -2 -3 -4 -4 -4 -5 -6 -7 -8 -7 -7 -8 -9 -9 -10 -12 -12 -13 -14 -15 -16 -18 -19 -20 -20 -19 -20 -20 -20 -20 -20 -21 -19 -18 -16 -15 -12 -9 -8 -7 -5 -3 -1 0 1 3 4 4 4 5 5 5 6 6 7 … ]} {[QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T … ]}
{[ 7 7 7 7 8 8 8 8 8 8 9 9 9 9 9 10 11 12 13 14 15 16 18 22 26 27 26 25 25 23 21 18 15 12 11 10 8 6 5 6 7 8 9 10 10 10 10 10 9 8 6 5 5 5 6 7 8 8 7 8 11 14 15 15 13 11 7 6 6 8 9 11 12 11 10 12 20 29 42 57 72 86 96 107 113 119 115 106 91 72 57 44 36 30 25 18 12 7 5 5 4 2 0 0 0 -1 -2 -3 -3 -3 -4 -4 -5 -7 -9 -10 -10 -11 -12 -13 -14 -16 -18 -19 -20 -21 -23 -23 -24 -25 -25 -26 -26 -26 -25 -24 -22 -21 -20 -18 -16 -14 -12 -9 -8 -7 -5 -2 -1 0 1 2 2 1 2 2 2 2 3 4 3 4 4 5 4 4 4 5 6 6 7 8 9 10 14 18 20 21 21 21 20 18 16 12 7 4 3 3 1 -1 -2 -3 -3 -2 0 0 0 0 0 0 0 -1 -2 -2 -3 -4 -3 -2 -2 -1 0 1 2 4 5 4 3 0 -3 -5 -4 -3 -1 1 0 0 0 2 7 16 30 45 58 70 80 90 97 102 102 94 81 63 47 32 22 18 15 9 1 -3 -5 -7 -8 -9 -9 -10 -11 -11 -11 -11 -12 -13 -12 -13 -14 -17 -17 -18 -19 -19 -20 -20 -21 -23 -24 -25 -27 -28 -28 -28 -28 -29 -30 -31 -31 -32 -31 -31 -31 -28 -26 -24 -23 -22 -20 -17 -15 -13 -11 -9 -8 -7 -5 -3 -3 -2 -2 -1 -1 -1 -1 0 0 -1 0 0 1 1 2 2 1 0 1 1 3 4 6 8 9 12 15 17 18 17 17 16 13 10 8 4 3 2 2 1 0 -1 -1 0 1 2 3 5 4 3 2 1 1 0 0 0 0 0 0 0 0 1 2 4 7 7 5 4 2 0 -2 -3 -3 -2 -1 0 -1 -3 -2 4 13 24 36 51 63 73 82 90 98 101 97 86 69 52 36 26 21 18 15 10 4 1 0 -1 -2 -2 -2 -3 -3 -4 -5 -5 -5 -6 -6 -7 -7 -8 -9 -9 -10 -11 -11 -11 -12 -13 -14 -15 -16 -17 -18 -19 -20 -21 -20 -19 -19 -19 -19 -17 -16 -15 -14 -12 -9 -8 -5 -4 -2 -2 0 3 5 6 7 7 8 8 8 8 8 7 8 9 9 9 9 10 10 10 11 11 11 11 11 12 14 14 15 17 19 20 22 24 25 24 24 23 22 19 15 13 10 10 9 9 7 8 9 10 10 9 10 11 11 10 11 11 10 9 9 9 8 8 9 10 10 10 12 14 16 16 15 14 11 7 5 4 4 4 5 7 6 6 7 13 22 32 46 61 74 86 96 108 114 116 110 96 78 61 49 40 35 30 25 19 13 10 8 7 6 6 6 6 5 4 4 4 3 3 3 3 2 1 0 0 -1 -2 -2 -3 -3 -5 -5 -6 -7 -9 -10 -10 -11 -12 -13 -13 -13 -13 -12 -12 -11 -10 -8 -5 -3 -2 -1 0 2 4 7 10 12 13 14 14 13 13 12 12 12 12 12 11 11 11 10 11 11 10 9 9 8 7 8 10 12 13 15 17 20 22 24 24 22 21 20 20 17 13 9 8 8 6 4 2 0 1 4 6 6 4 2 2 2 2 2 1 1 1 0 0 0 0 0 0 1 1 4 7 8 7 5 2 0 -4 -4 -3 -2 -1 0 1 0 0 5 16 28 43 58 74 87 99 109 117 121 115 103 83 66 50 39 34 28 21 13 8 6 3 2 1 0 -1 -2 -2 -2 -3 -4 -4 -5 -6 -7 -7 -7 -7 -8 -9 -10 -12 -13 -13 -15 -16 -17 -17 -18 -19 -20 -22 -23 -24 -25 -26 -26 -26 -25 -24 -22 -21 -20 -18 -15 -13 -11 -7 -5 -4 -2 -1 0 1 1 1 2 2 3 3 4 3 3 5 4 4 3 4 4 4 4 3 3 3 3 4 6 7 7 9 13 16 17 17 17 17 17 16 14 10 5 0 -1 -1 -3 -5 -6 -6 -6 -7 -5 -5 -5 -6 -4 -3 -4 -7 -8 -9 -10 -9 -8 -8 -9 -9 -10 -10 -9 -7 -4 -2 -2 -4 -7 -10 -14 -16 -16 -14 -13 -12 -12 -13 -11 -5 5 19 36 53 72 87 102 111 121 123 112 95 72 52 34 24 20 14 6 -2 -7 -9 -10 -10 -11 -13 -15 -16 -16 -17 -18 -18 -18 -18 -19 -20 -21 -22 -23 -24 -25 -26 -28 -29 -29 -30 -31 -34 -36 -37 -38 -38 -39 -39 -41 -42 -44 -44 -43 -42 -40 -38 -38 -36 -32 -29 -27 -24 -21 -20 -19 -17 -15 -12 -12 -10 -9 -9 -9 -9 -8 -8 -9 -8 -7 -7 -7 -7 -6 -7 -9 -9 -8 -7 -7 -5 -3 -2 -1 0 3 6 9 12 13 12 11 11 10 6 1 -3 -5 -7 -9 -10 -11 -12 -12 -11 -10 -10 -9 -8 -7 -8 -9 -9 -9 -10 -11 -11 -10 -10 -11 -10 -9 -9 -8 -5 -3 -3 -5 -6 -9 -12 -13 -14 -13 -12 -10 -8 -7 -7 -3 6 19 31 47 63 77 89 99 109 112 112 101 85 66 46 32 24 20 14 8 1 -2 -5 -6 -6 -7 -8 -8 -8 -8 -10 -11 -11 -11 -12 -13 -13 -14 -15 -15 -15 -16 -17 -18 -18 -19 -20 -20 -20 -22 -24 -26 -25 -26 -26 -26 -26 -27 -27 -26 -25 -23 -22 -19 -17 -15 -14 -12 -10 -8 -6 -4 -2 -1 0 0 1 2 2 3 4 4 3 3 4 4 5 5 6 6 6 6 6 6 6 7 8 9 9 10 13 15 17 20 23 25 24 23 23 22 20 17 13 10 8 8 7 4 2 2 3 4 5 5 5 5 5 6 6 4 3 3 3 3 3 3 3 3 4 4 6 8 10 11 9 6 2 0 -1 -2 -1 0 1 2 0 0 2 10 19 31 46 60 72 82 92 99 102 103 93 80 64 48 34 26 23 20 14 8 4 3 2 1 0 0 0 -1 -2 -2 -2 -2 -3 -3 -3 -3 -4 -5 -5 -5 -6 -6 -7 -8 -9 -10 -11 -12 -13 -14 -15 -16 -17 -16 -16 -16 -17 -17 -16 -16 -14 -12 -10 -9 -7 -4 -2 0 1 3 5 7 8 9 11 12 12 13 13 13 13 13 13 12 12 13 13 13 13 13 14 14 14 14 15 15 16 18 20 21 23 26 29 30 31 31 30 29 26 23 18 14 13 12 12 9 8 8 9 10 11 11 10 10 10 11 11 10 9 8 8 7 6 7 7 7 8 10 11 12 13 14 12 10 8 6 4 4 4 5 6 5 4 6 10 17 29 43 56 69 79 90 97 102 106 106 99 85 69 51 38 30 27 25 18 12 8 7 7 5 5 5 5 4 4 4 3 2 2 2 1 0 0 0 0 -1 -1 -2 -4 -5 -5 -6 -7 -9 -9 -10 -11 -13 -13 -13 -14 -15 -15 -15 -15 -14 -13 -11 -9 -7 -5 -4 -2 0 2 4 5 6 8 10 10 10 11 11 11 10 11 12 12 12 12 13 12 11 12 13 13 13 14 15 16 16 17 18 19 23 26 29 29 29 29 29 27 24 21 17 14 11 10 9 7 7 7 9 9 9 10 11 10 9 9 9 8 7 7 7 6 6 5 6 6 6 8 10 12 13 12 11 8 5 2 1 0 0 2 3 3 2 4 8 15 26 41 57 71 84 96 107 115 119 116 104 85 66 49 38 31 28 23 16 10 6 5 4 2 2 2 2 1 0 0 -1 -2 -3 -2 -2 -2 -3 -3 -5 -6 -7 -8 -8 -10 -11 -12 -13 -13 -15 -16 -18 -19 -20 -19 -19 -18 -18 -18 -17 -16 -15 -13 -11 -9 -7 -4 -1 1 2 4 7 8 10 12 13 13 13 14 14 14 14 15 15 14 13 13 14 15 15 15 16 16 16 16 18 18 19 20 22 24 26 28 30 31 31 31 31 30 28 24 21 18 17 15 14 12 11 13 15 16 15 15 16 16 15 15 15 14 13 11 12 12 12 12 13 13 13 13 15 18 19 18 17 15 12 10 9 8 8 8 8 8 7 7 13 21 30 43 57 71 81 91 102 108 113 109 99 84 67 52 40 35 30 26 20 14 11 9 10 9 8 7 7 6 5 5 4 4 3 3 3 2 1 1 1 0 0 -1 -1 -2 -4 -4 -4 -5 -7 -8 -8 -9 -10 -11 -11 -11 -12 -11 -9 -7 -7 -5 -3 -2 -1 1 4 5 7 10 12 12 13 14 16 16 15 15 16 16 16 17 … ]} {[T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a … ]}
Choose to Train Networks or Download Pre-Trained Networks
The next sections of this example compare three different approaches to train LSTM networks. Due to the large size of the dataset, the training process of each network may take several minutes. If your machine has a GPU and Parallel Computing Toolbox™, then MATLAB automatically uses the GPU for faster training. Otherwise, it uses the CPU.
You can skip the training steps and download the pre-trained networks using the selector below. If you want to train the networks as the example runs, select 'Train Networks'. If you want to skip the training steps, select 'Download Networks' and a file containing all three pre-trained networks -rawNet, filteredNet, and fsstNet- will be downloaded into your temporary directory, whose location is specified by MATLAB®'s tempdir command. If you want to place the downloaded file in a folder different from tempdir, change the directory name in the subsequent instructions.
actionFlag ="Train networks"; if actionFlag == "Download networks" % Download the pre-trained networks dataURL = 'https://ssd.mathworks.com/supportfiles/SPT/data/QTDatabaseECGSegmentationNetworks.zip'; %#ok<*UNRCH> modelsFolder = fullfile(tempdir,'QTDatabaseECGSegmentationNetworks'); modelsFile = fullfile(modelsFolder,'trainedNetworks.mat'); zipFile = fullfile(tempdir,'QTDatabaseECGSegmentationNetworks.zip'); if ~exist(modelsFolder,'dir') websave(zipFile,dataURL); unzip(zipFile,fullfile(tempdir,'QTDatabaseECGSegmentationNetworks')); end load(modelsFile) end
Results between the downloaded networks and newly trained networks may vary slightly since the networks are trained using random initial weights.
Input Raw ECG Signals Directly into the LSTM Network
First, train an LSTM network using the raw ECG signals from the training dataset.
Define the network architecture before training. Specify a sequenceInputLayer of size 1 to accept one-dimensional time series. Specify an LSTM layer with the 'sequence' output mode to provide classification for each sample in the signal. Use 200 hidden nodes for optimal performance. Specify a fullyConnectedLayer with an output size of 4, one for each of the waveform classes. Add a softmaxLayer and a classificationLayer to output the estimated labels.
layers = [ ... sequenceInputLayer(1) lstmLayer(200,'OutputMode','sequence') fullyConnectedLayer(4) softmaxLayer classificationLayer];
Choose options for the training process that ensure good network performance. Refer to the trainingOptions (Deep Learning Toolbox) documentation for a description of each parameter.
options = trainingOptions('adam', ... 'MaxEpochs',10, ... 'MiniBatchSize',50, ... 'InitialLearnRate',0.01, ... 'LearnRateDropPeriod',3, ... 'LearnRateSchedule','piecewise', ... 'GradientThreshold',1, ... 'Plots','training-progress',... 'shuffle','every-epoch',... 'Verbose',0,... 'DispatchInBackground',true);
Because the entire training dataset fits in memory, it is possible to use the tall function of the datastore to transform the data in parallel, if Parallel Computing Toolbox™ is available, and then gather it into the workspace. Neural network training is iterative. At every iteration, the datastore reads data from files and transforms the data before updating the network coefficients. If the data fits into the memory of your computer, importing the data into the workspace enables faster training because the data is read and transformed only once. Note that if the data does not fit in memory, you must to pass the datastore into the training function, and the transformations are performed at every training epoch.
Create tall arrays for both the training and test sets. Depending on your system, the number of workers in the parallel pool that MATLAB creates may be different.
tallTrainSet = tall(trainDs);
Starting parallel pool (parpool) using the 'Processes' profile ... Connected to the parallel pool (number of workers: 8).
tallTestSet = tall(testDs);
Now call the gather function of the tall arrays to compute the transformations over the entire dataset and obtain cell arrays with the training and test signals and labels.
trainData = gather(tallTrainSet);
Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 10 sec Evaluation completed in 11 sec
trainData(1,:)
ans=1×2 cell array
{[0 0 0 0 0 0 1 1 1 1 1 1 0 1 2 1 1 2 2 2 3 4 6 8 11 15 18 18 17 17 17 16 14 12 8 4 2 1 0 -1 -2 -1 0 0 0 1 2 2 2 2 1 0 -1 -1 -2 -3 -3 -2 -2 -2 -1 0 4 5 5 3 2 0 -1 -1 0 2 3 5 5 3 4 8 15 25 36 50 63 73 83 90 97 99 98 88 74 58 42 30 22 19 15 10 5 1 -1 -2 -2 -3 -4 -5 -6 -7 -9 -9 -10 -12 -13 -13 -12 -13 -14 -15 -15 -16 -18 -19 -20 -21 -22 -21 -22 -23 -24 -25 -25 -26 -27 -28 -29 -29 -28 -26 -25 -24 -23 -21 -19 -18 -16 -14 -12 -11 -9 -7 -6 -5 -5 -3 -3 -3 -3 -2 -2 -2 -2 -1 -1 -2 -2 -1 -1 -1 -1 0 0 0 -1 0 1 2 3 5 7 8 11 13 13 13 12 11 9 6 2 0 -2 -3 -5 -7 -8 -8 -7 -5 -4 -5 -4 -3 -4 -4 -5 -5 -6 -8 -9 -9 -8 -9 -9 -8 -6 -6 -4 -2 -3 -4 -5 -6 -7 -8 -8 -7 -6 -5 -6 -8 -7 -5 2 12 24 36 48 58 66 72 78 83 82 75 61 46 30 18 11 9 6 0 -4 -8 -9 -11 -12 -12 -13 -13 -14 -14 -15 -17 -17 -17 -17 -18 -18 -18 -19 -21 -22 -23 -23 -25 -25 -26 -26 -27 -28 -29 -30 -31 -32 -32 -33 -33 -34 -34 -34 -34 -32 -31 -30 -29 -27 -25 -23 -22 -19 -17 -15 -15 -14 -12 -11 -11 -9 -8 -8 -8 -8 -9 -9 -8 -8 -8 -8 -9 -8 -7 -7 -8 -8 -7 -7 -7 -6 -5 -3 -3 -1 2 4 5 6 7 6 5 4 2 -2 -5 -7 -7 -8 -10 -10 -10 -10 -9 -9 -7 -7 -6 -5 -5 -6 -8 -10 -11 -12 -12 -11 -11 -11 -10 -9 -7 -6 -5 -6 -7 -9 -11 -13 -14 -14 -14 -12 -11 -10 -11 -10 -6 0 10 22 35 47 58 68 76 80 83 78 67 51 36 22 12 6 3 -1 -6 -10 -12 -13 -14 -16 -17 -17 -17 -18 -18 -18 -19 -20 -20 -20 -20 -20 -19 -19 -20 -21 -22 -23 -25 -26 -26 -26 -26 -27 -27 -28 -28 -29 -28 -29 -28 -28 -29 -28 -27 -25 -25 -23 -22 -21 -19 -17 -15 -14 -12 -10 -9 -8 -7 -6 -5 -5 -5 -5 -5 -5 -5 -4 -4 -4 -3 -3 -3 -4 -3 -3 -3 -3 -4 -3 -4 -4 -2 -1 0 2 4 8 10 10 10 10 9 8 6 4 0 -3 -5 -5 -7 -9 -9 -8 -7 -8 -8 -7 -7 -7 -6 -6 -6 -7 -9 -9 -10 -11 -11 -11 -10 -10 -9 -7 -5 -3 -4 -5 -7 -9 -10 -11 -9 -8 -6 -4 -3 -4 -6 -5 0 6 16 27 40 51 60 68 75 82 81 77 66 52 39 27 17 10 6 2 -2 -6 -10 -12 -13 -14 -15 -16 -15 -16 -16 -17 -17 -17 -18 -18 -18 -17 -17 -16 -17 -17 -18 -19 -19 -20 -20 -21 -22 -23 -24 -25 -26 -26 -26 -26 -27 -26 -26 -26 -25 -24 -23 -22 -21 -19 -18 -16 -14 -11 -9 -8 -7 -5 -4 -4 -3 -2 -1 -1 -1 -1 -1 -2 -1 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 4 5 7 10 14 16 17 15 14 13 12 11 8 5 1 0 0 -2 -4 -4 -3 -3 -2 -1 0 0 0 -1 -2 -3 -5 -5 -5 -6 -6 -5 -5 -5 -4 -2 0 1 2 1 0 -3 -5 -5 -5 -4 -2 0 0 -1 -1 1 7 14 26 39 53 63 73 81 87 90 87 80 65 51 38 26 18 12 8 3 -2 -6 -8 -9 -10 -11 -12 -12 -12 -14 -13 -12 -12 -13 -13 -14 -15 -16 -17 -16 -17 -18 -18 -17 -18 -20 -21 -22 -22 -24 -24 -24 -24 -24 -24 -23 -24 -24 -24 -23 -22 -21 -19 -16 -14 -13 -11 -9 -7 -5 -3 0 0 1 2 3 4 4 4 6 6 6 6 7 8 7 7 7 7 6 6 8 8 8 8 9 9 9 10 11 12 12 14 15 17 19 22 25 27 27 27 27 25 22 19 15 13 11 11 10 9 8 7 8 8 8 9 9 10 10 9 9 7 5 5 6 6 5 5 5 6 6 9 12 13 11 9 6 4 1 1 4 6 7 9 9 8 9 14 23 34 48 62 77 86 96 103 109 110 103 92 76 61 45 34 29 25 19 11 6 2 0 0 -1 -3 -5 -6 -6 -6 -7 -7 -7 -7 -8 -8 -8 -9 -10 -11 -11 -11 -12 -14 -15 -15 -16 -17 -17 -18 -19 -20 -21 -21 -22 -22 -21 -21 -20 -19 -18 -16 -15 -13 -11 -9 -7 -4 -1 1 2 4 5 6 7 8 9 9 9 9 9 9 9 8 9 10 10 11 12 12 11 11 11 11 10 11 11 12 13 14 15 15 15 17 20 24 28 29 30 29 28 28 27 24 20 16 14 13 12 11 10 9 8 9 9 9 9 10 11 11 10 9 8 7 7 6 6 6 6 7 7 8 10 12 13 11 8 5 3 1 0 2 5 6 6 5 4 6 12 22 35 50 62 77 88 97 103 108 110 104 94 78 62 45 34 29 26 21 14 9 5 3 1 0 -1 -2 -3 -4 -4 -5 -6 -6 -5 -6 -8 -8 -8 -8 -9 -10 -10 -12 -13 -14 -15 -15 -16 -17 -17 -19 -21 -22 -22 -23 -24 -24 -23 -24 -24 -22 -20 -19 -17 -14 -12 -10 -9 -7 -5 -4 -3 -1 1 3 4 5 7 7 7 8 8 8 7 7 8 7 7 7 7 5 5 5 5 5 5 6 7 7 7 7 8 9 10 11 13 16 18 20 21 20 20 19 18 15 12 9 7 6 4 3 2 2 2 2 3 2 1 2 3 4 3 3 2 1 0 0 -1 -1 -2 -2 -1 0 1 2 2 0 -3 -5 -8 -9 -9 -8 -6 -5 -6 -6 -5 -1 7 20 35 49 62 74 84 92 99 105 103 94 77 58 39 25 19 16 12 6 0 -3 -6 -9 -11 -12 -12 -14 -14 -14 -14 -15 -15 -16 -17 -17 -18 -17 -17 -18 -18 -19 -20 -22 -23 -23 -24 -26 -27 -28 -29 -30 -31 -30 -31 -31 -33 -33 -33 -32 -30 -30 -28 -27 -25 -22 -20 -18 -16 -13 -10 -8 -6 -4 -2 -2 -2 -1 0 -1 0 0 0 0 0 1 0 0 0 1 1 1 0 1 2 2 2 3 3 3 4 5 6 7 9 13 16 19 19 19 18 18 17 16 13 9 6 4 3 1 0 -2 -2 -2 -1 0 0 1 1 1 1 0 0 0 -2 -3 -3 -2 -3 -3 -4 -2 -1 0 1 1 0 -2 -5 -6 -9 -9 -7 -5 -3 -1 -1 0 2 8 18 32 46 59 71 83 94 101 107 106 98 83 65 49 35 27 23 21 15 7 2 0 0 -2 -4 -4 -6 -7 -8 -8 -9 -9 -9 -8 -9 -9 -10 -9 -10 -11 -11 -11 -12 -13 -14 -15 -16 -18 -18 -19 -20 -21 -22 -23 -24 -24 -24 -24 -24 -24 -23 -21 -19 -17 -16 -14 -11 -9 -7 -5 -2 -1 1 2 2 2 3 4 4 4 4 4 4 4 5 5 4 3 4 5 5 4 4 4 4 5 5 7 6 6 6 7 8 9 12 15 19 20 21 19 18 18 18 16 12 8 5 4 4 2 1 0 0 0 1 3 3 3 4 4 4 3 2 1 1 0 0 1 1 0 1 1 2 3 3 3 1 0 -1 -3 -5 -5 -3 -1 0 0 0 1 4 10 21 34 47 60 71 82 89 97 100 100 93 80 66 47 34 26 23 19 13 7 3 1 -1 -2 -3 -4 -6 -7 -6 -6 -6 -6 -6 -6 -7 -8 -9 -9 -9 -10 -10 -11 -12 -14 -15 -16 -17 -18 -19 -19 -21 -21 -22 -23 -24 -25 -25 -24 -23 -23 -21 -20 -19 -18 -16 -12 -10 -7 -5 -4 -3 -2 -1 0 1 1 2 2 2 1 1 1 0 0 1 1 0 0 1 1 1 1 2 3 4 3 3 3 3 4 5 7 7 8 11 13 15 16 16 16 15 14 12 10 7 4 3 2 0 0 0 1 0 0 0 1 1 2 3 3 1 0 0 -1 -2 -3 -2 -2 -1 -1 0 0 1 2 2 1 -1 -4 -6 -7 -7 -6 -5 -4 -4 -5 -3 0 5 14 27 42 56 67 79 87 96 101 105 101 87 71 53 39 29 24 22 16 10 5 2 1 0 -1 -2 -3 … ]} {[n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a P P P P P P P P P P P P P P P P P P P P n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a n/a QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS QRS n/a n/a n/a n/a n/a n/a n/a n/a T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T T n/a n/a n/a n/a n/a n/a n/a n/a … ]}
testData = gather(tallTestSet);
Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 2.9 sec Evaluation completed in 3 sec
Train Network
Use the trainNetwork command to train the LSTM network.
if actionFlag == "Train networks" rawNet = trainNetwork(trainData(:,1),trainData(:,2),layers,options); end
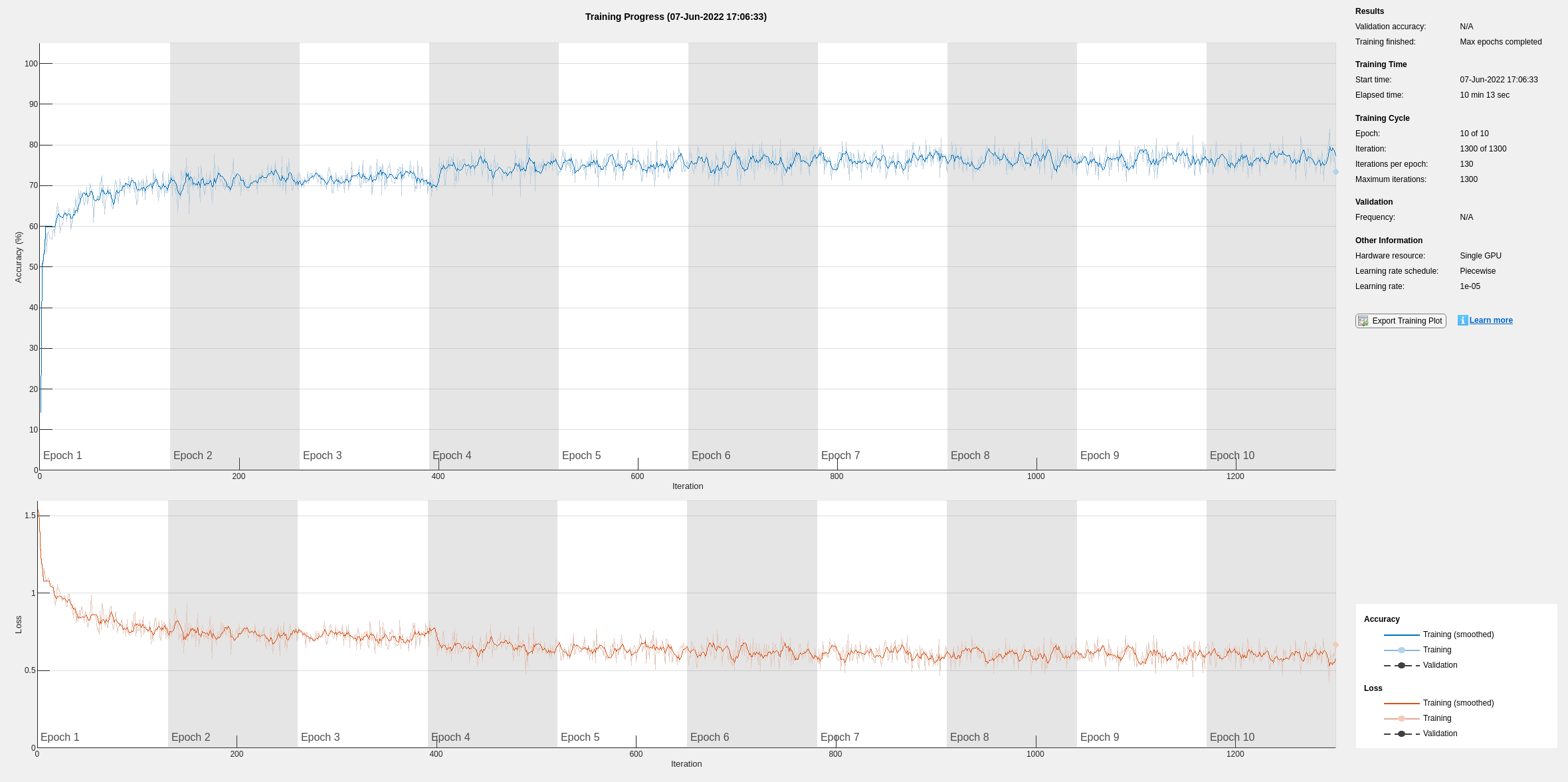
The training accuracy and loss subplots in the figure track the training progress across all iterations. Using the raw signal data, the network correctly classifies about 77% of the samples as belonging to a P wave, a QRS complex, a T wave, or an unlabeled region "n/a".
Classify Testing Data
Classify the testing data using the trained LSTM network and the classify command. Specify a mini-batch size of 50 to match the training options.
predTest = classify(rawNet,testData(:,1),'MiniBatchSize',50);A confusion matrix provides an intuitive and informative means to visualize classification performance. Use the confusionchart command to calculate the overall classification accuracy for the testing data predictions. For each input, convert the cell array of categorical labels to a row vector. Specify a row-normalized display to view results as percentages of samples for each class.
confusionchart([testData{:,2}],[predTest{:}],'Normalization','row-normalized');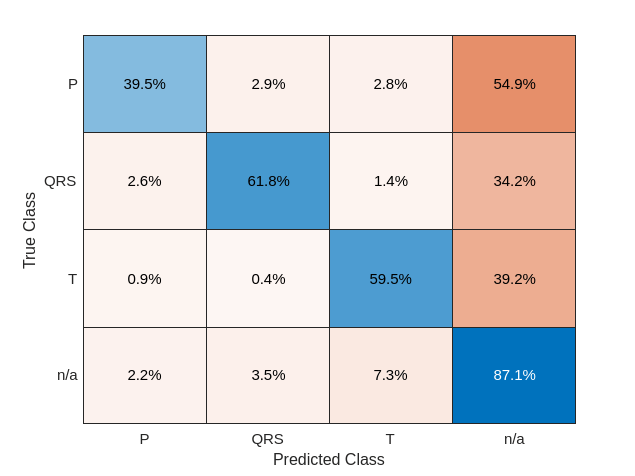
Using the raw ECG signal as input to the network, only about 60% of T-wave samples, 40% of P-wave samples, and 60% of QRS-complex samples were correct. To improve performance, apply some knowledge of the ECG signal characteristics prior to input to the deep learning network, for instance the baseline wandering caused by a patient's respiratory motion.
Apply Filtering Methods to Remove Baseline Wander and High-Frequency Noise
The three beat morphologies occupy different frequency bands. The spectrum of the QRS complex typically has a center frequency around 10–25 Hz, and its components lie below 40 Hz. The P and T waves occur at even lower frequencies: P-wave components are below 20 Hz, and T-wave components are below 10 Hz [5].
Baseline wander is a low-frequency (< 0.5 Hz) oscillation caused by the patient's breathing motion. This oscillation is independent from the beat morphologies and does not provide meaningful information [6].
Design a bandpass filter with passband frequency range of [0.5, 40] Hz to remove the wander and any high frequency noise. Removing these components improves the LSTM training because the network does not learn irrelevant features. Use cellfun on the tall data cell arrays to filter the dataset in parallel.
% Bandpass filter design hFilt = designfilt('bandpassiir', 'StopbandFrequency1',0.4215,'PassbandFrequency1', 0.5, ... 'PassbandFrequency2',40,'StopbandFrequency2',53.345,... 'StopbandAttenuation1',60,'PassbandRipple',0.1,'StopbandAttenuation2',60,... 'SampleRate',250,'DesignMethod','ellip'); % Create tall arrays from the transformed datastores and filter the signals tallTrainSet = tall(trainDs); tallTestSet = tall(testDs); filteredTrainSignals = gather(cellfun(@(x)filter(hFilt,x),tallTrainSet(:,1),'UniformOutput',false));
Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 11 sec Evaluation completed in 11 sec
trainLabels = gather(tallTrainSet(:,2));
Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 3.3 sec Evaluation completed in 3.7 sec
filteredTestSignals = gather(cellfun(@(x)filter(hFilt,x),tallTestSet(:,1),'UniformOutput',false));Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 2.4 sec Evaluation completed in 2.5 sec
testLabels = gather(tallTestSet(:,2));
Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 1.9 sec Evaluation completed in 2.1 sec
Plot the raw and filtered signals for a typical case.
trainData = gather(tallTrainSet);
Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 3.8 sec Evaluation completed in 4.1 sec
figure
subplot(2,1,1)
plot(trainData{95,1}(2001:3000))
title('Raw')
grid
subplot(2,1,2)
plot(filteredTrainSignals{95}(2001:3000))
title('Filtered')
grid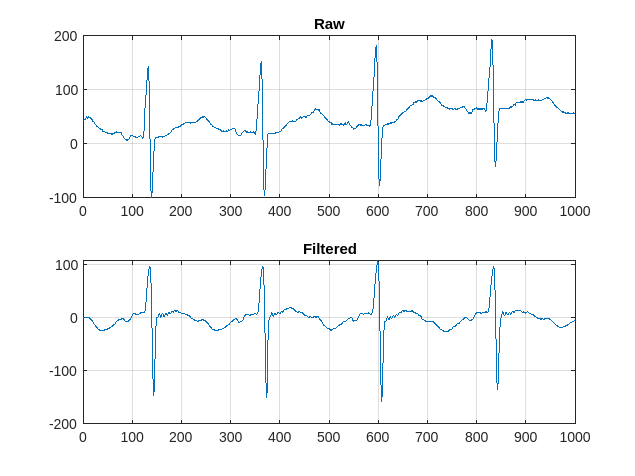
Even though the baseline of the filtered signals may confuse a physician that is used to traditional ECG measurements on medical devices, the network will actually benefit from the wandering removal.
Train Network with Filtered ECG Signals
Train the LSTM network on the filtered ECG signals using the same network architecture as before.
if actionFlag == "Train networks" filteredNet = trainNetwork(filteredTrainSignals,trainLabels,layers,options); end
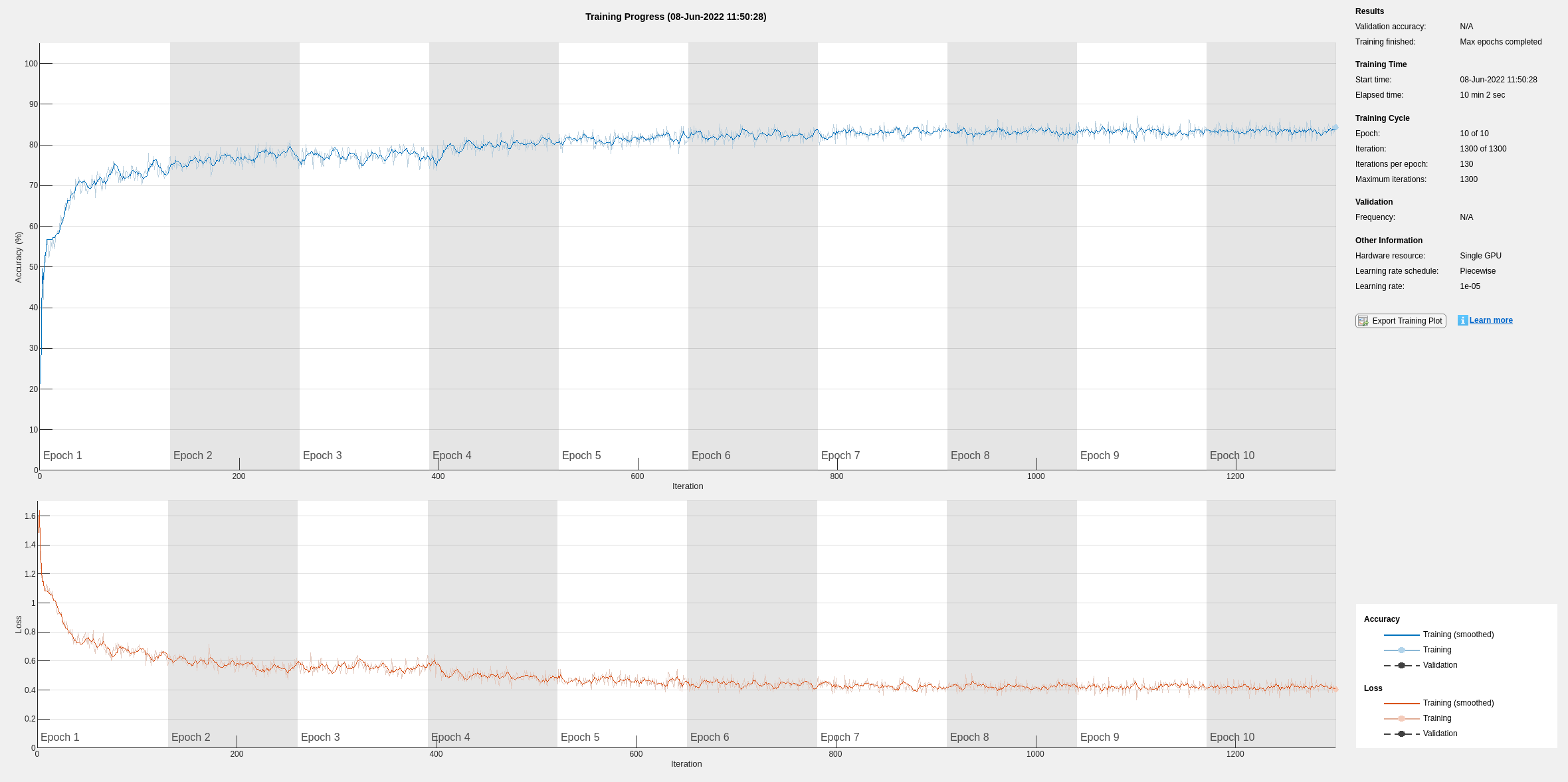
Preprocessing the signals improves the training accuracy to better than 80%.
Classify Filtered ECG Signals
Classify the preprocessed test data with the updated LSTM network.
predFilteredTest = classify(filteredNet,filteredTestSignals,'MiniBatchSize',50);Visualize the classification performance as a confusion matrix.
figure
confusionchart([testLabels{:}],[predFilteredTest{:}],'Normalization','row-normalized');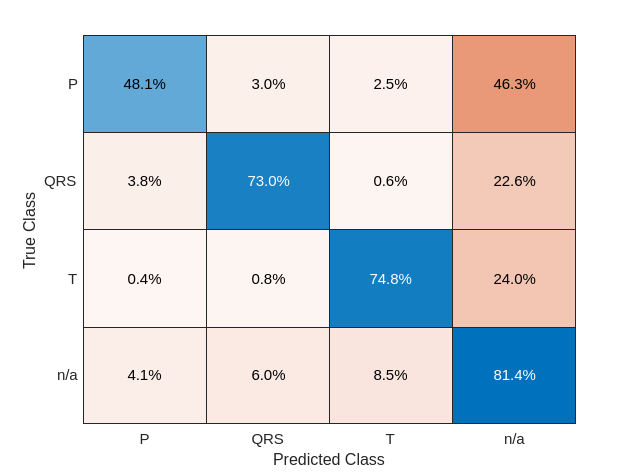
Simple preprocessing improves T-wave classification by about 15%, and QRS-complex and P-wave classification by about 10%.
Time-Frequency Representation of ECG Signals
A common approach for successful classification of time-series data is to extract time-frequency features and feed them to the network instead of the original data. The network then learns patterns across time and frequency simultaneously [7].
The Fourier synchrosqueezed transform (FSST) computes a frequency spectrum for each signal sample so it is ideal for the segmentation problem at hand where we need to maintain the same time resolution as the original signals. Use the fsst function to inspect the transform of one of the training signals. Specify a Kaiser window of length 128 to provide adequate frequency resolution.
data = preview(trainDs);
figure
fsst(data{1,1},250,kaiser(128),'yaxis')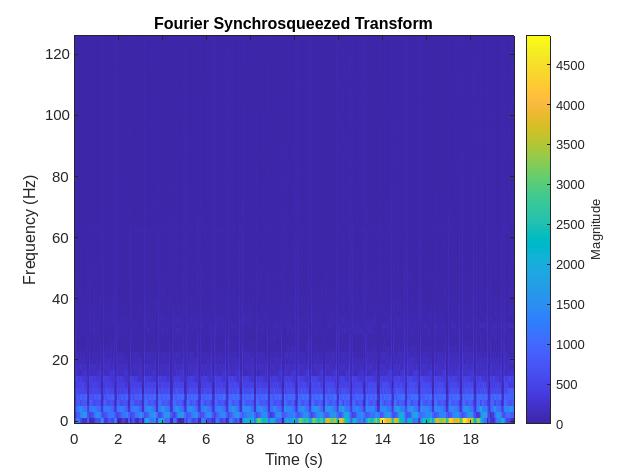
Calculate the FSST of each signal in the training dataset over the frequency range of interest, [0.5, 40] Hz. Treat the real and imaginary parts of the FSST as separate features and feed both components into the network. Furthermore, standardize the training features by subtracting the mean and dividing by the standard deviation. Use a transformed datastore, the extractFSSTFeatures helper function, and the tall function to process the data in parallel.
fsstTrainDs = transform(trainDs,@(x)extractFSSTFeatures(x,250)); fsstTallTrainSet = tall(fsstTrainDs); fsstTrainData = gather(fsstTallTrainSet);
Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: 0% complete Evaluation 0% complete - Pass 1 of 1: 4% complete Evaluation 4% complete - Pass 1 of 1: 8% complete Evaluation 8% complete - Pass 1 of 1: 12% complete Evaluation 12% complete - Pass 1 of 1: 17% complete Evaluation 17% complete - Pass 1 of 1: 21% complete Evaluation 21% complete - Pass 1 of 1: 25% complete Evaluation 25% complete - Pass 1 of 1: 29% complete Evaluation 29% complete - Pass 1 of 1: 33% complete Evaluation 33% complete - Pass 1 of 1: 38% complete Evaluation 38% complete - Pass 1 of 1: 42% complete Evaluation 42% complete - Pass 1 of 1: 46% complete Evaluation 46% complete - Pass 1 of 1: 50% complete Evaluation 50% complete - Pass 1 of 1: 54% complete Evaluation 54% complete - Pass 1 of 1: 58% complete Evaluation 58% complete - Pass 1 of 1: 62% complete Evaluation 62% complete - Pass 1 of 1: 67% complete Evaluation 67% complete - Pass 1 of 1: 71% complete Evaluation 71% complete - Pass 1 of 1: 75% complete Evaluation 75% complete - Pass 1 of 1: 79% complete Evaluation 79% complete - Pass 1 of 1: 83% complete Evaluation 83% complete - Pass 1 of 1: 88% complete Evaluation 88% complete - Pass 1 of 1: 92% complete Evaluation 92% complete - Pass 1 of 1: 96% complete Evaluation 96% complete - Pass 1 of 1: 100% complete Evaluation 100% complete - Pass 1 of 1: Completed in 2 min 39 sec Evaluation 100% complete Evaluation completed in 2 min 39 sec
Repeat this procedure for the testing data.
fsstTTestDs = transform(testDs,@(x)extractFSSTFeatures(x,250)); fsstTallTestSet = tall(fsstTTestDs); fsstTestData = gather(fsstTallTestSet);
Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 1 min 8 sec Evaluation completed in 1 min 8 sec
Adjust Network Architecture
Modify the LSTM architecture so that the network accepts a frequency spectrum for each sample instead of a single value. Inspect the size of the FSST to see the number of frequencies.
size(fsstTrainData{1,1})ans = 1×2
40 5000
Specify a sequenceInputLayer of 40 input features. Keep the rest of the network parameters unchanged.
layers = [ ... sequenceInputLayer(40) lstmLayer(200,'OutputMode','sequence') fullyConnectedLayer(4) softmaxLayer classificationLayer];
Train Network with FSST of ECG Signals
Train the updated LSTM network with the transformed dataset.
if actionFlag == "Train networks" fsstNet = trainNetwork(fsstTrainData(:,1),fsstTrainData(:,2),layers,options); end
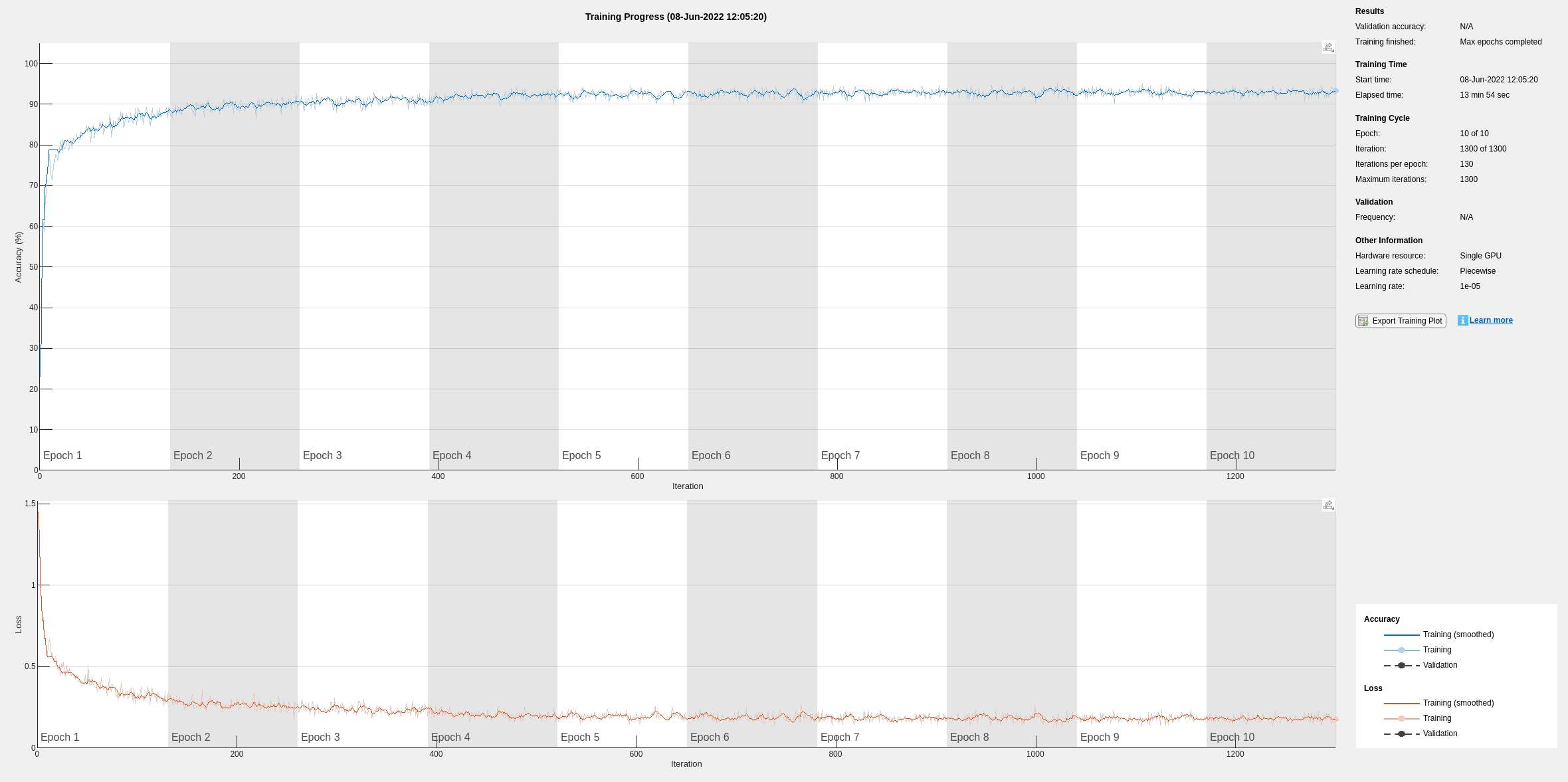
Using time-frequency features improves the training accuracy, which now exceeds 90%.
Classify Test Data with FSST
Using the updated LSTM network and extracted FSST features, classify the testing data.
predFsstTest = classify(fsstNet,fsstTestData(:,1),'MiniBatchSize',50);Visualize the classification performance as a confusion matrix.
confusionchart([fsstTestData{:,2}],[predFsstTest{:}],'Normalization','row-normalized');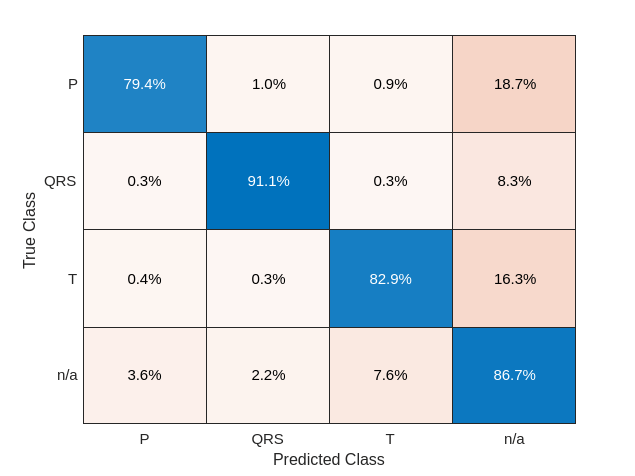
Using a time-frequency representation improves T-wave classification by about 25%, P-wave classification by about 40%, and QRS-complex classification by 30%, when compared to the raw data results.
Use a signalMask object to compare the network prediction to the ground truth labels for a single ECG signal. Ignore the "n/a" labels when plotting the regions of interest.
testData = gather(tall(testDs));
Evaluating tall expression using the Parallel Pool 'Processes': - Pass 1 of 1: Completed in 2.1 sec Evaluation completed in 2.2 sec
Mtest = signalMask(testData{1,2}(3000:4000));
Mtest.SpecifySelectedCategories = true;
Mtest.SelectedCategories = find(Mtest.Categories ~= "n/a");
figure
subplot(2,1,1)
plotsigroi(Mtest,testData{1,1}(3000:4000))
title('Ground Truth')
Mpred = signalMask(predFsstTest{1}(3000:4000));
Mpred.SpecifySelectedCategories = true;
Mpred.SelectedCategories = find(Mpred.Categories ~= "n/a");
subplot(2,1,2)
plotsigroi(Mpred,testData{1,1}(3000:4000))
title('Predicted')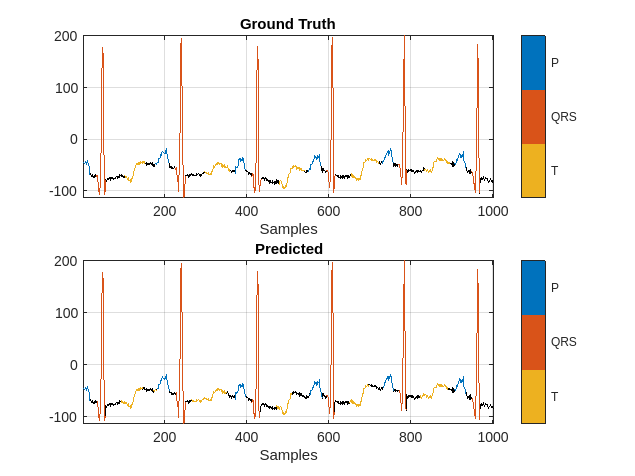
Conclusion
This example showed how signal preprocessing and time-frequency analysis can improve LSTM waveform segmentation performance. Bandpass filtering and Fourier-based synchrosqueezing result in an average improvement across all output classes from 55% to around 85%.
References
[1] McSharry, Patrick E., et al. "A dynamical model for generating synthetic electrocardiogram signals." IEEE® Transactions on Biomedical Engineering. Vol. 50, No. 3, 2003, pp. 289–294.
[2] Laguna, Pablo, Raimon Jané, and Pere Caminal. "Automatic detection of wave boundaries in multilead ECG signals: Validation with the CSE database." Computers and Biomedical Research. Vol. 27, No. 1, 1994, pp. 45–60.
[3] Goldberger, Ary L., Luis A. N. Amaral, Leon Glass, Jeffery M. Hausdorff, Plamen Ch. Ivanov, Roger G. Mark, Joseph E. Mietus, George B. Moody, Chung-Kang Peng, and H. Eugene Stanley. "PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals." Circulation. Vol. 101, No. 23, 2000, pp. e215–e220. [Circulation Electronic Pages; http://circ.ahajournals.org/content/101/23/e215.full].
[4] Laguna, Pablo, Roger G. Mark, Ary L. Goldberger, and George B. Moody. "A Database for Evaluation of Algorithms for Measurement of QT and Other Waveform Intervals in the ECG." Computers in Cardiology. Vol.24, 1997, pp. 673–676.
[5] Sörnmo, Leif, and Pablo Laguna. "Electrocardiogram (ECG) signal processing." Wiley Encyclopedia of Biomedical Engineering, 2006.
[6] Kohler, B-U., Carsten Hennig, and Reinhold Orglmeister. "The principles of software QRS detection." IEEE Engineering in Medicine and Biology Magazine. Vol. 21, No. 1, 2002, pp. 42–57.
[7] Salamon, Justin, and Juan Pablo Bello. "Deep convolutional neural networks and data augmentation for environmental sound classification." IEEE Signal Processing Letters. Vol. 24, No. 3, 2017, pp. 279–283.
See Also
Functions
confusionchart(Deep Learning Toolbox) |fsst|labeledSignalSet|lstmLayer(Deep Learning Toolbox) |trainingOptions(Deep Learning Toolbox) |trainnet(Deep Learning Toolbox)
Related Topics
- Long Short-Term Memory Neural Networks (Deep Learning Toolbox)
- Sequence-to-Sequence Regression Using Deep Learning (Deep Learning Toolbox)
- Sequence-to-Sequence Classification Using Deep Learning (Deep Learning Toolbox)
