Uncertain LTI Dynamics Elements
Uncertain linear, time-invariant objects, ultidyn, are used to represent unknown linear, time-invariant dynamics, whose
only known attributes are bounds on their frequency response.
Create Uncertain LTI Dynamics
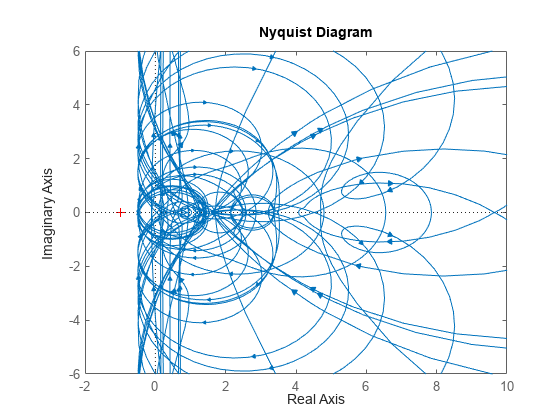
You can create a 1-by-1 (scalar) positive-real uncertain linear dynamics element, whose frequency response always has real part greater than -0.5. Set the SampleStateDimension property to 5. Plot a Nyquist plot of 30 instances of the element.
g = ultidyn('g',[1 1],'Type','Positivereal','Bound',-0.5); g.SampleStateDimension = 5;
nyquist(usample(g,30)) xlim([-2 10]) ylim([-6 6]);
Properties of ultidyn Elements
Uncertain linear, time-invariant objects have an internal name (the
Name property), and are created by specifying their size (number of
outputs and number of inputs).
The property Type specifies whether the known attributes about the
frequency response are related to gain or phase. The property Type may be
'GainBounded' or 'PositiveReal'. The default value
is 'GainBounded'.
The property Bound is a single number, which along with
Type, completely specifies what is known about the uncertain frequency
response. Specifically, if Δ is an ultidyn element, and if γ denotes the value of the Bound
property, then the element represents the set of all stable, linear, time-invariant systems
whose frequency response satisfies certain conditions:
If Type is 'GainBounded', for all frequencies. When Type is
'GainBounded', the default value for Bound (i.e.,
γ) is 1. The NominalValue of Δ is always the
0-matrix.
If Type is 'PositiveReal', Δ(ω) + Δ*(ω) ≥ 2γ· for all frequencies. When Type is
'PositiveReal', the default value for Bound (i.e.,
γ) is 0. The NominalValue is always (γ + 1 +2|γ|)I.
All properties of a ultidyn are accessible with
get and set (although the
NominalValue is determined from Type and
Bound, and not accessible with set). The properties
are
|
Properties |
Meaning |
Class |
|---|---|---|
|
|
Internal Name |
|
|
|
Nominal value of element |
|
|
|
|
|
|
|
Norm bound or minimum real |
|
|
|
State-space dimension of random samples of this uncertain element |
|
|
|
Maximum natural frequency for random sampling |
|
|
|
|
|
The SampleStateDim property specifies the state dimension of random
samples of the element when using usample. The default value is 1. The
AutoSimplify property serves the same function as in the uncertain real
parameter.
Time Domain of ultidyn Elements
On its own, every ultidyn element is interpreted as a
continuous-time, system with uncertain behavior, quantified by bounds (gain or real-part) on
its frequency response. However, when a ultidyn element is an uncertain
element of an uncertain state space model (uss), then the time-domain characteristic of the element is determined from
the time-domain characteristic of the system. The bounds (gain-bounded or positivity) apply
to the frequency-response of the element.
Interpreting Uncertainty in Discrete Time
The interpretation of a ultidyn element as a continuous-time or
discrete-time system depends on the nature of the uncertain system (uss) within which it is an uncertain element.
For example, create a scalar ultidyn object. Then, create two
1-input, 1-output uss objects using the ultidyn object as their “D” matrix. In one case, create without
specifying sample-time, which indicates continuous time. In the second case, force
discrete-time, with a sample time of 0.42.
delta = ultidyn('delta',[1 1]);
sys1 = uss([],[],[],delta)
USS: 0 States, 1 Output, 1 Input, Continuous System
delta: 1x1 LTI, max. gain = 1, 1 occurrence
sys2 = uss([],[],[],delta,0.42)
USS: 0 States, 1 Output, 1 Input, Discrete System, Ts = 0.42
delta: 1x1 LTI, max. gain = 1, 1 occurrence
Next, get a random sample of each system. When obtaining random samples using usample, the values of the elements used in the sample are returned in the 2nd
argument from usample as a structure.
[sys1s,d1v] = usample(sys1); [sys2s,d2v] = usample(sys2);
Look at d1v.delta.Ts and d2v.delta.Ts. In the
first case, since sys1 is continuous-time, the system
d1v.delta is continuous-time. In the second case, since
sys2 is discrete-time, with sample time 0.42, the system
d2v.delta is discrete-time, with sample time 0.42.
d1v.delta.Ts
ans =
0
d2v.delta.Ts
ans =
0.4200
Finally, in the case of a discrete-time uss object, it is not the case that ultidyn objects are interpreted as continuous-time uncertainty in feedback
with sampled-data systems. This very interesting hybrid theory is beyond the scope of the
toolbox.