h2hinfsyn
Mixed H2/H∞ synthesis with regional pole placement constraints
Description
[
employs LMI techniques to compute an output-feedback control law u =
K(s)y for the control problem of the following illustration. K,CL,normz,info]
= h2hinfsyn(P,Nmeas,Ncon,Nz2,Wz,Name,Value)
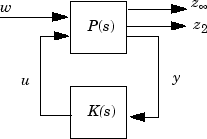
The LTI plant P has partitioned state-space form given
by
The resulting controller K:
Keeps the H∞ norm G of the transfer function from w to z∞ below the value you specify using the
Name,Valueargument'HINFMAX'.Keeps the H2 norm H of the transfer function from w to z2 below the value you specify using the
Name,Valueargument'H2MAX'.Minimizes a tradeoff criterion of the form
where W1 and W2 are the first and second entries in the vector
Wz.Places the closed-loop poles in the LMI region that you specify using the
Name,Valueargument'REGION'.
Use the input arguments Nmeas, Ncon, and
Nz2 to specify the number of signals in
y, u, and
z2, respectively. You can use
additional Name,Value pairs to specify additional options for
the computation.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
Do not choose weighting functions with poles very close to s = 0 (z = 1 for discrete-time systems). For instance, although it might seem sensible to choose W = 1/s to enforce zero steady-state error, doing so introduces an unstable pole that cannot be stabilized, causing synthesis to fail. Instead, choose W = 1/(s + δ). The value δ must be small but not very small compared to system dynamics. For instance, for best numeric results, if your target crossover frequency is around 1 rad/s, choose δ = 0.0001 or 0.001. Similarly, in discrete time, choose sample times such that system and weighting dynamics are not more than a decade or two below the Nyquist frequency.
References
[1] Chilali, M., and P. Gahinet, “H∞ Design with Pole Placement Constraints: An LMI Approach,” IEEE Trans. Aut. Contr., 41 (1995), pp. 358–367.
[2] Scherer, C., “Mixed H2/H-infinity Control,” Trends in Control: A European Perspective, Springer-Verlag (1995), pp.173–216.
Version History
Introduced before R2006a